Нейтральная ось композитного стержня.
 Будем считать, что при том нейтральная ось стержня перейдет в некое другое положение. Согласно предположению Бернулли сохраним гипотезу плоских сечений, согласно которой изогнутое сечение не сжимается в поперечном направлении и остается плоским и перпендикулярным нейтральной оси, которая расположена на расстоянии
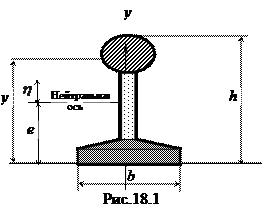
Будем считать, что при том нейтральная ось стержня перейдет в некое другое положение. Согласно предположению Бернулли сохраним гипотезу плоских сечений, согласно которой изогнутое сечение не сжимается в поперечном направлении и остается плоским и перпендикулярным нейтральной оси, которая расположена на расстоянии  от нижней кромки (Рис. 18.1)
от нижней кромки (Рис. 18.1)
Продольные перемещения в любом волокне слоистого стержня
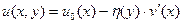 , (18.1)
, (18.1)
где 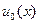 осевое перемещение точек нейтральной оси,
осевое перемещение точек нейтральной оси,  - прогиб сечения, а
- прогиб сечения, а 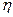 (y) - расстояние описываемого тонкого волокна от нейтральной оси (Рис.18.1). Далее обозначения упараметров координаты «y» за очевидностью опускаем.
(y) - расстояние описываемого тонкого волокна от нейтральной оси (Рис.18.1). Далее обозначения упараметров координаты «y» за очевидностью опускаем.
Относительная деформация в продольном направлении 
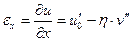 (18.2)
(18.2)
порождает нормальные напряжения
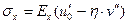 . (18.3)
. (18.3)
Для поперечного сечения, находящегося в сжато-изогнутом состоянии, нормальные напряжения приводятся к осевой силе
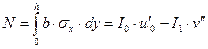 (18.4)
(18.4)
и к изгибающему моменту 
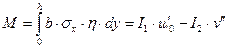 , (18.5)
, (18.5)
где
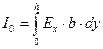 ,
, 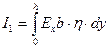 ,
, 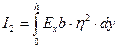 . (18.6)
. (18.6)
Теперь найдем положение нейтральной оси из условия, что ось не изгибается,
то есть, продольные усилия в сечении связываются только с деформацией нейтральной оси 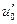 , а изгибающий момент - только с кривизной оси
, а изгибающий момент - только с кривизной оси 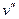 . Положим в (18.4)
. Положим в (18.4) 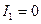 и учтем, что
и учтем, что 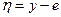 . Получим
. Получим
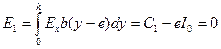 , (18.7)
, (18.7)
где обозначено
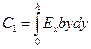 (18.8)
(18.8)
Теперь из (18.7) получаем положение нейтральной оси
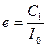 (18.9)
(18.9)
Теперь соотношения (18. 4), (18. 5) принимают вид
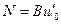 ,
, 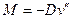 , (18.10)
, (18.10)
где с учетом (18. 9) обозначено
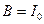 ,
,
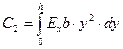 (18.10)
(18.10)
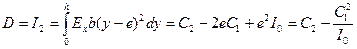
Из (18.3), (18.10) получаем такое окончательное выражение для напряжений
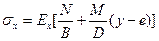
 (18.11)
(18.11)
Здесь B и D, аналогично теории изотропных стержней, обозначают жесткости на растяжение-сжатие и изгиб. Они, так же как координата нейтральной оси и изгибная жесткость стержня, вычисляются через параметры сечения.
Для изотропного стержня с b=const из материала с модулем E имеем

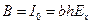 ,
, 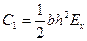 ,
, 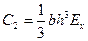 ,
, 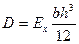 ,
, 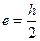 .
.
Слоистый стержень.
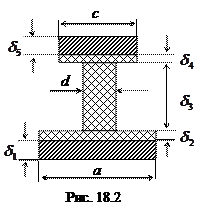
Рассмотрим общий случай слоистого стержня (Рис18.2)
Здесь n – количество слоев,
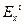 ,
, 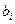 - модуль и толщина i-гослоя,
- модуль и толщина i-гослоя,
 - расстояние от нижней кромки сечения до
- расстояние от нижней кромки сечения до
верхней кромки i-гослоя, при этом 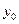 = 0, а
= 0, а 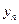 = h, параметры e и D определяются по формулам (18.7), (18.9), модуль стержня
= h, параметры e и D определяются по формулам (18.7), (18.9), модуль стержня 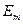 , модули накладок
, модули накладок 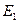 и
и 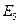 .
.
Таким образом примем:
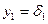 ,
, 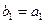 ,
, 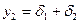 ,
, 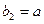 , и т. д.
, и т. д.
Для параметров стержня имеем:
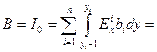

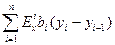 ,
,
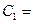
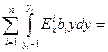

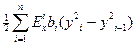 , (18.12)
, (18.12)
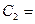
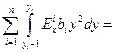
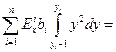
 ,
,
Уравнение изгиба композиционной балки поперечной нагрузкой q полностью аналогично сопромату
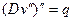 ,
,
только изгибная жесткость определяется формлуой (18.11).
Устойчивость слоистой балки описывается уравнением

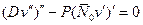 ,
,
полностью идентичным рассмотренным ранее.
Критическая сила в задаче Эйлера
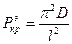 .
.
Таким образом, слоистые стержни расчитываются аналогично однородным, однако предварительно нужно найти параметры (18.12).
Дата добавления: 2016-09-06; просмотров: 1588;










