Устойчивость стержней за пределами упругости
Все, изложенное до сих пор, справедливо при условии, что выполняются все принятые гипотезы и, в частности, гипотеза о том, что как в докритическом состоянии, так и в момент потери устойчивости, т.е. при выпучивании материал остается идеально и линейно упругим. Однако, у грамотно спроектированного стержня критические напряжения должны быть близки к 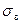
 . Тогда они будут превышать предел пропорциональности
. Тогда они будут превышать предел пропорциональности 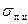 , и, следовательно, полученные формулы будут уже несправедливы.
, и, следовательно, полученные формулы будут уже несправедливы.
|
|
Эксперименты показывают, что отклонения 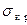 от
от 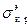 , незначительные при
, незначительные при 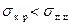
 , становятся при
, становятся при 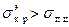 существенными и имеют значительный разброс. Нестабильность результатов объясняется разбросом физических свойств материала образцов за пределами упругости.
существенными и имеют значительный разброс. Нестабильность результатов объясняется разбросом физических свойств материала образцов за пределами упругости.
Парабола на рис.12.1 соответствует формуле Эйлера
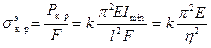 . (12.1)
. (12.1)
Величину
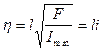 ,
,
где 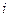 - радиус инерции, называют “гибкостью” стержня.
- радиус инерции, называют “гибкостью” стержня.
За пределами пропорциональности 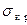 иногда аппроксимируют полуэмпирически с помощью различных формул. Например (Рис.12.2)
иногда аппроксимируют полуэмпирически с помощью различных формул. Например (Рис.12.2)
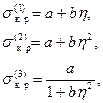
подбирая константы 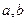 экспериментально.
экспериментально.
Рассмотрим теоретические подходы к  оценке
оценке 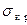 при известной диаграмме
при известной диаграмме 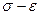 .
.
Записав формулу Эйлера (12.1) в безразмерном виде
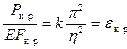 , (12.2)
, (12.2)
мы фактически имеем критическое значение не силы, а деформации. По этому значению находим на диаграмме точку, соответствующую моменту потери устойчивости. Однако, значение 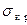 с этой диаграммы непосредственно снять нельзя, поскольку формула (12.2) получена в предположении о линейности диаграммы.
с этой диаграммы непосредственно снять нельзя, поскольку формула (12.2) получена в предположении о линейности диаграммы.
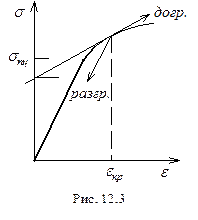
|
При выпучивании стержня его поперечное сечение по одну сторону от нейтральной оси догружается, а по другую - разгружается. Следовательно, модули упругости материала в этих зонах могут быть разными.
Догрузка в малой окрестности точки выпучивания на диаграмме будет происходить по касательной к кривой, а разгрузка по прямой, почти параллельной линейному участку. Соответствующие модули называют “касательным” - 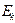 и “секущим” -
и “секущим” - 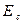 .
.
Даже если считать, что разгрузка и догрузка происходят с 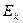 , т.е. предположить материал нелинейно, но идеально упругим, то замена в формуле Эйлера
, т.е. предположить материал нелинейно, но идеально упругим, то замена в формуле Эйлера 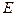 на
на 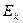 даст cущественное уточнение результата, которым можно ограничиться. Если же учесть разницу
даст cущественное уточнение результата, которым можно ограничиться. Если же учесть разницу 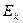 и
и 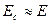 , то ясно, что точки, не испытывающие изгибных напряжений, будут лежать на оси, уже не проходящей через центр масс сечения.
, то ясно, что точки, не испытывающие изгибных напряжений, будут лежать на оси, уже не проходящей через центр масс сечения.
|
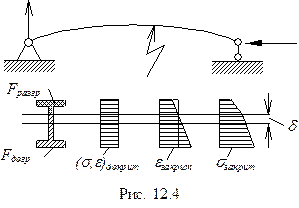
Предположим, что напряженно-деформированное состояние по всей длине стержня имеет одну и ту же картину (рис.12.4). Вообще говоря, это не так, ибо max напряжения по длине переменны.
Предположим также, что в процессе выпучивания нагрузка, прикладываемая к стержню, не меняется.
Тогда закритические изгибные напряжения должны давать нулевую результирующую силу
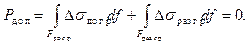
Здесь 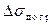 и
и 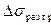 изгибные напряжения, действующие в зоне догрузки
изгибные напряжения, действующие в зоне догрузки 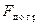 и разгрузки
и разгрузки 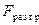 . Считая, что сечение остается плоским, имеем
. Считая, что сечение остается плоским, имеем
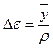 ,
,
где 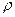 - радиус кривизны стержня,
- радиус кривизны стержня, 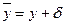 - расстояние до закритической нейтральной оси.
- расстояние до закритической нейтральной оси.
Тогда
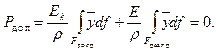
В итоге имеем
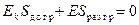 , (12.3)
, (12.3)
где 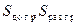 - статические моменты догруженной и разгруженной зон относительно смещенной нейтральной оси. Соотношение (12.3) служит для определения
- статические моменты догруженной и разгруженной зон относительно смещенной нейтральной оси. Соотношение (12.3) служит для определения 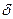 .
.
Очевидно, что величина 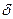 будет зависеть от формы поперечного сечения.
будет зависеть от формы поперечного сечения.
Оценим влияние формы поперечного сечения на величину 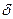 на двух примерах.
на двух примерах.
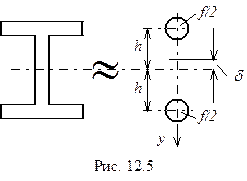
|
I. Пусть сечение имеет форму двутавра с настолько тонкой стенкой, что напряжениями 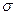 в ней можно пренебречь. Тогда расчетная модель сечения будет иметь вид, изображенный на рис.12.5.
в ней можно пренебречь. Тогда расчетная модель сечения будет иметь вид, изображенный на рис.12.5.
В этом случае 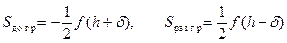
и из (12.3) имеем
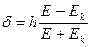 . (12.4)
. (12.4)
II. Для сплошного прямоугольного сечения высотой  площадью
площадью  будем иметь
будем иметь
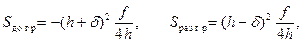
и из (12.3)
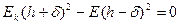 . (12.5)
. (12.5)
При реальных 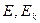 величина
величина 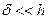 .
.
Пренебрегая в (12.5) величиной 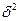 по сравнению с
по сравнению с 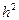 , имеем
, имеем
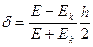 . (12.6)
. (12.6)
Определив положение нейтральной оси, можно найти внутренний изгибающий момент в сечении
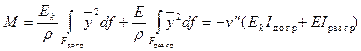 . (12.7)
. (12.7)
Введем обозначение для приведенного модуля
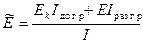 , (12.8)
, (12.8)
где 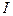 - центральный момент инерции сечения. С учетом (12.8) выражение (12.7) записывается в традиционном виде
- центральный момент инерции сечения. С учетом (12.8) выражение (12.7) записывается в традиционном виде
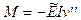 .
.
Таким образом, для определения 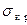 в формуле (12.1) модуль
в формуле (12.1) модуль 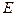 надо заменить на приведенный
надо заменить на приведенный 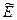 .
.
Дата добавления: 2016-09-06; просмотров: 2221;











