Устойчивость стержней при их нагружении следящей силой

Рассматривая влияние на устойчивость упругих стержней различных отклонений от идеализированной схемы, мы оставляли незыблемым соглашение о том, что в процессе возможной изгибной деформации стержня нагрузка остается “мертвой”, т.е. не меняет ни величины, ни направления.

Как было показано в Лекции 4 на примере систем с одной и двумя степенями свободы, т.е. систем, состоящих из недеформируемых стержней, следящая нагрузка может влиять на критическую нагрузку не только количественно, но и качественно.

Рассмотрим наиболее наглядный пример существенного влияния характера нагрузки на устойчивость стержня (рис.11.1). Критическое значение “мертвой” нагрузки для такого стержня .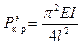

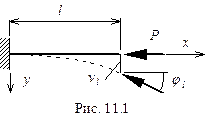
Дифференциальное уравнение упругой линии стержня в случае следящей силы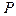

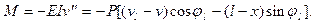
Его линеаризованный вариант

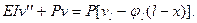(11.1)

Общее решение этого уравнения 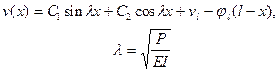(11.2)

содержит четыре произвольные постоянные, определяемые из граничных условий

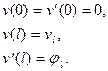(11.3)

Подчиняя (11.2) условиям (11.3), получаем однородную систему

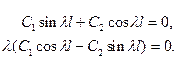
Определитель этой системы

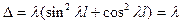
не обращается в нуль ни при каких 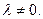Это означает, что рассматриваемый упругий стержень, как и жесткий с упругой заделкой при нагружении следящей силой, не имеет форм равновесия, близких к исходной.

Как отмечалось в Лекции 4, полученный результат целесообразно проверить с позиций динамического критерия устойчивости.

C этой целью запишем уравнение динамического равновесия стержня в искривленном состоянии, внеся в условие статического равновесия (5.9) инерционную поперечную нагрузку

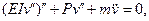(11.4)

где 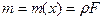- погонная масса стержня с поперечным сечением 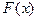, сделанного из материала плотностью .

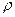Ограничившись случаем постоянных коэффициентов, запишем (11.4) в виде

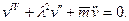
(11.5)

Это уравнение колебаний сжатого стержня.

Его решение можно получить методом разделения переменных в виде

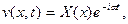(11.6)

где 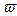- частота колебаний.

Если в результате поиска решения в виде (11.6) окажется, что - действительна, то это будет означать, что стержень совершает гармонические изгибные колебания, т.е. мы имеем случай устойчивого равновесия.

(11.7)

Если 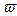будет мнимой, т.е.

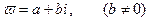(11.8)

то

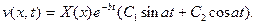(11.9)

Это означает, что стержень будет колебаться в зависимости от знака либо с затухающей амплитудой ( равновесие устойчиво), либо с нарастающей амплитудой ( 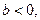равновесие неустойчиво).

Подставим (11.6) в (11.5). Введя безразмерные параметры

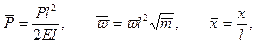
запишем

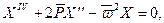(11.10)

где штрихом обозначена производная по .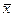

Общее решение уравнения (11.10)

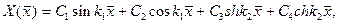(11.11)

где

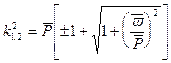(11.12)

Граничные условия в заделке 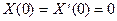дают

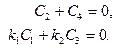(11.13)

Граничные условия на правом конце 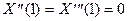дают

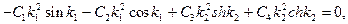
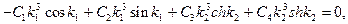
или с учетом (11.12)

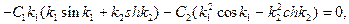
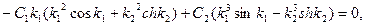(11.14)

Приравняем нулю определитель системы (11.14)

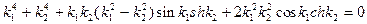
или с учетом (11.12)

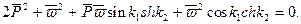(11.14)

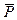Уравнение (11.14) служит для определения при фиксированном . Наименьшее из значений 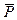, при котором корни 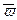уравнения (11.14) перестают быть действительными и различными, а становятся кратными, будет тем “пороговым” значением, при превышении которого корни станут комплексно-сопряженными 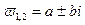, т.е. амплитуда колебаний станет нарастать.

Такое значение отыскивается численно 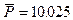и дает критическую силу

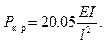(11.15)

Графически зависимость от , обусловленная уравнением (11.14), представлена на рис.11.2.

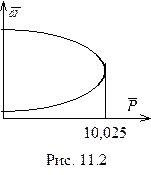
При этой силе стержень, искривленный любым случайным образом, начнет колебаться с возрастающей амплитудой.

Поскольку в рассмотренном примере мы имеем дело с динамическим характером потери устойчивости, естественно предположить, что распределение масс вдоль стержня должно влиять на величину критической нагрузки, как это было в примере 4.1. C другой стороны, при “мертвой” нагрузке динамический критерий устойчивости должен давать тот же результат, что и статический критерий, при использовании которого распределение масс по стержню нигде не фигурирует и, следовательно, на результат не влияет.

Чтобы разобраться в этом вопросе, рассмотрим предыдущий пример, приняв другую массовую модель. Будем считать стержень “бесплотным”, а в точке 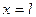поместим некоторую сосредоточенную массу 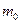(рис.11.3).

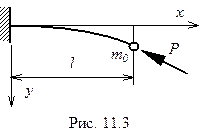
Тогда в уравнении (11.5) погонную массу 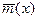можно представить в виде

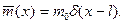
Уравнение (11.10) для этого случая примет вид

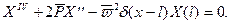
Его общее решение можно получить способом, изложенным в [7]. Но в данном частном случае, когда сосредоточенная масса расположена на конце стержня, проще поступить иначе.

Рассмотрим обычное уравнение устойчивости

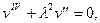(11.16)

где, однако, .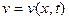

Его общее решение

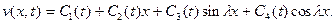(11.17)

Константы будем искать из граничных условий, три из которых

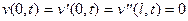(11.18)

не отличаются от условий в статической постановке, а четвертое -

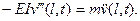(11.19)

Подчиним (11.17) условиям (11.18),(11.19), приняв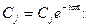

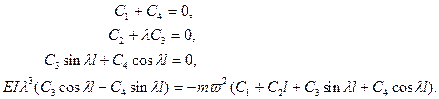
Приравняв нулю определитель этой системы, получим

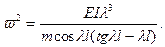(11.20)

Проанализируем выражение (11.20).

Поскольку числитель обращается в нуль только при 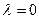, а знаменатель не обращается в бесконечность ни при каких 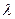, равновесие 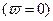возможно только при отсутствии нагрузки.

В интервале 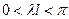знаменатель положителен и 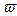- действительна, что соответствует гармоническим колебаниям и, следовательно, устойчивому равновесию. При 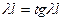знаменатель меняет знак, 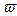становится чисто мнимой, амплитуда отклонения начинает нарастать, равновесие становится неустойчивым.

Соотношение

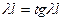
дает 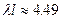, что соответствует

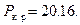(11.21)

Сопоставляя (11.15), (11.21), убеждаемся, что замена одной массовой модели стержня на другую отразилась на значении критической силы.

Если бы нагрузка оставалась “мертвой”, то в граничное условие (11.19) вошла бы проекция силы 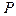на нормаль к упругой оси

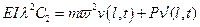
Это условие имело бы вид

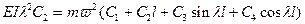
или с учетом условий (11.18)

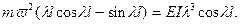(11.22)

Из (11.22) следует, что система может иметь 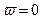, т.е. находится в искривленном положении равновесия при условии

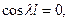
т.е. 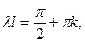что соответствует

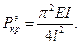
Мы получили тот же результат, что и при статическом подходе, т.е. при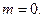

Таким образом, можно сделать следующий вывод.

При “мертвой” нагрузке динамический подход приводит к тому же результату, что и статический. Этот результат не зависит от распределения масс по стержню.

При “следящей” нагрузке не происходит потери статической устойчивости в том смысле, что система не имеет искривленных положений равновесия.

Критическая сила, приводящая к “раскачке” стержня, может быть найдена с помощью динамического критерия. Эта сила зависит от распределения масс вдоль стержня. При этом близость результатов (11.21) и (11.15) не дает основания утверждать, что зависимость 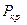от распределения масс слабая, поскольку, перемещая сосредоточенную массу к заделке, мы можем получить сколь угодно большую критическую силу.

Вопрос в том, по какому признаку можно заранее утверждать, что статический критерий не позволит найти критическую силу, до сих пор остается дискуссионным [6]. Ясно, что статический критерий всегда применим, если система консервативна, т.е. работа приложенных к ней сил не зависит от траектории точек приложения этих сил. Но сам этот факт зачастую можно установить, только решив задачу.

Для динамической картины потери устойчивости необходимо, чтобы процесс отклонения системы от исходного положения равновесия сопровождался подводом энергии извне. Это - другой признак неконсервативности системы.