Тема 2. Теоремы сложения и умножения вероятностей. Условная вероятность
1. Вероятность суммы несовместных событий
Теорема. Если  и
и 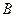 – несовместные события, то справедлива формула
– несовместные события, то справедлива формула
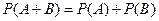
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.
Следствие. Если 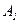 ,
, 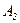 ,...,
,..., 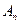 – попарно несовместные события, то справедлива формула
– попарно несовместные события, то справедлива формула
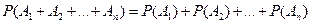 .
.
Пример 1. Из колоды, содержащей 36 карт, наудачу вынимают 3 карты. Найти вероятность того, что среди них окажется хотя бы одна «дама»?
Решение. Обозначим
 – из 3-х выбранных карт окажется хотя бы одна «дама»,
– из 3-х выбранных карт окажется хотя бы одна «дама»,
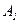 – из 3-х выбранных карт окажется одна «дама»,
– из 3-х выбранных карт окажется одна «дама»,
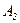 – из 3-х выбранных карт окажется две «дамы»,
– из 3-х выбранных карт окажется две «дамы»,
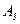 – из 3-х выбранных карт окажется три «дамы».
– из 3-х выбранных карт окажется три «дамы».
Тогда 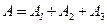 , причем события
, причем события 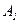 ,
, 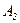 ,
, 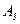 – несовместные. Поэтому
– несовместные. Поэтому
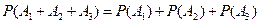 .
.
Число возможных случаев выбора трех карт из 36 равно 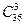 . Число случаев, благоприятных событиям
. Число случаев, благоприятных событиям 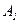 ,
, 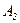 ,
, 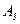 , соответственно равны
, соответственно равны
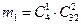 ,
, 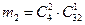 ,
, 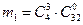 .
.
Таким образом,
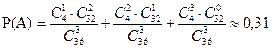 .
.
Задача решается проще, если воспользоваться формулой вероятности противоположного события.
Событие 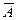 - среди выбранных карт нет ни одной дамы.
- среди выбранных карт нет ни одной дамы.
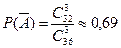 .
.
Значит искомая вероятность
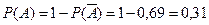 .
.
2. Теорема умножения вероятностей
Событие  называется независимым от события
называется независимым от события 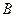 , если вероятность события
, если вероятность события  не зависит от того, произошло событие
не зависит от того, произошло событие 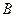 или нет. Событие
или нет. Событие  называется зависимым от события
называется зависимым от события 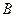 , если вероятность события
, если вероятность события  меняется в зависимости от того, произошло событие
меняется в зависимости от того, произошло событие 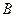 или нет.
или нет.
Вероятность события  , вычисленная при условии, что имело место другое событие
, вычисленная при условии, что имело место другое событие 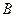 , называется условной вероятностью события
, называется условной вероятностью события  и обозначается
и обозначается 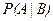 или
или 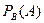 . Читается так: вероятность события
. Читается так: вероятность события  при условии, что произошло событие
при условии, что произошло событие 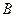 .
.
Пример 2. Брошена игральная кость. Событие  - выпала цифра 4.
- выпала цифра 4.
Безусловная (обычная) вероятность 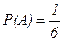 .
.
Пусть известно, что произошло событие 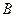 – выпала четная цифра (т.е. 2, 4, 6) – всего три возможных исхода. Событию
– выпала четная цифра (т.е. 2, 4, 6) – всего три возможных исхода. Событию  благоприятствует один из них – цифра 4, следовательно, условная вероятность
благоприятствует один из них – цифра 4, следовательно, условная вероятность 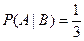 .
.
Теорема. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:
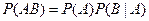 или
или 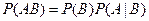 .
.
Если событие  не зависит от события
не зависит от события 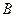 , то и событие
, то и событие 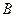 не зависит от события
не зависит от события  . Тогда
. Тогда
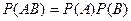 .
.
Пример 3. Выборка шаров без возвращения. Пусть в урне находится 10 шаров: 3 белых и 7 черных. Выбираем наудачу один шар; не возвращая его в урну, выбираем второй шар. С какой вероятностью оба шара будут белыми?
Решение. Пусть событие  заключается в том, что первый раз вынут белый шар, его вероятность
заключается в том, что первый раз вынут белый шар, его вероятность 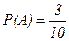 . Если событие
. Если событие  произошло, то в урне осталось 2 белых и 7 черных шаров. Вероятность того, что второй шар тоже является белым – это условная вероятность
произошло, то в урне осталось 2 белых и 7 черных шаров. Вероятность того, что второй шар тоже является белым – это условная вероятность 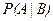 , она составляет
, она составляет 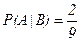 . Тогда по теореме умножения вероятностей
. Тогда по теореме умножения вероятностей
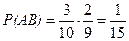 .
.
3. Вероятность суммы совместных событий
Теорема. Вероятность суммы двух совместных событий равна сумме их вероятностей без вероятности их произведения
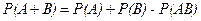 .
.
Пример 4. Бросают две игральные кости. Какова вероятность появления хотя бы одной шестерки?
Решение. Введем обозначения:
 – появление шестерки на первой кости,
– появление шестерки на первой кости,
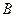 – появление шестерки на второй кости.
– появление шестерки на второй кости.
Тогда 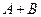 – появление хотя бы одной шестерки при бросании двух костей.
– появление хотя бы одной шестерки при бросании двух костей.
События  и
и 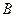 совместные. По формуле суммы двух совместных событий находим
совместные. По формуле суммы двух совместных событий находим
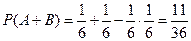 .
.
Дата добавления: 2016-09-06; просмотров: 2757;











