Примеры вычисления вероятностей

Пример 13. В ящике 10 перенумерованных шаров с номерами от 1 до 10. Вынули один шар. Какова вероятность того, что номер вынутого шара не превышает 10?

Решение. Так как номер любого шара, находящегося в ящике, не превышает 10, то число случаев, благоприятствующих событию , равно числу всех возможных случаев, т.е.

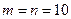и .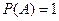

В этом случае событие достоверно.

Пример 14. В урне 15 шаров: 5 белых и 10 черных. Какова вероятность вынуть из урны синий шар?

Решение. Синих шаров в урне нет, т.е. 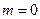, а 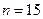. Следовательно, 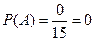. В данном случае событие - невозможное.

Пример 15. В урне 12 шаров: 3 белых, 4 черных и 5 красных. Какова вероятность вынуть из урны черный шар?

Решение. Здесь , .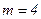

.

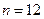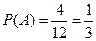Пример 16. В урне находятся 12 белых и 8 черных шаров. Найти вероятность того, что среди наугад вынутых 5 шаров 3 будут черными.

Решение. Событие – из 5 вынутых шаров три будут черными. Применим классическую формулу вероятностей

.

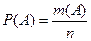Чтобы вычислить общее число исходов, необходимо вычислить количество способов выбора 5 шаров из всех шаров урны, т.е. из 20. Т.к. порядок извлечения шаров не важен, то используем формулу сочетаний без повторений .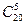

Определим число благоприятных исходов событию .

Из пяти вынутых шаров 3 шара должны быть черными, т.е. из 8-ми выбираем 3. Число таких выборов равно .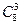

Оставшиеся 2 шара должны быть белыми, т.е. 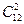. По правилу умножения получим .

.

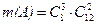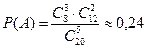Пример 17. Дано шесть карточек с буквами Н, М, И, Я, Л, О. Карточки перемешивают, берут по одной и кладут последовательно рядом. Найти вероятность того, что:

а) получится слово ЛОМ, если наугад одна за другой выбираются три карточки.

б) получится слово МОЛНИЯ, если выбраны все карточки.

Решение.

а) Из 6-ти данных букв можно составить 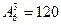трехбуквенных слов. Мы используем размещения, т.к. важен порядок извлекаемых букв, 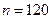. Слово ЛОМ появится только в одном случае .

.

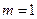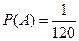б) Шестибуквенные слова отличаются только порядком их расположения, поэтому общее количество вариантов рассчитывается по формуле перестановок 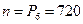. Слово МОЛНИЯ получится только в одном из этих случаев, т.е. 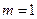, следовательно,

.

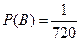Задачи для самостоятельного решения

1. Сколько существует четных пятизначных чисел, начинающихся нечетной цифрой?

2. Сколькими способами можно обить 8 стульев, если имеется 3 вида ткани. Считать, что все стулья одинаковые.

3. Сколькими способами можно выбрать наборы, состоящие из 2 карандашей и 3 ручек из пяти различных карандашей и шести различных ручек?

4. Кодовый замок может содержать любые 4 цифры. Каких кодовых номеров больше: в которых все цифры разные или в которых имеются хотя бы 2 одинаковые цифры.

5. 9 команд участвуют в спортивных соревнованиях. Сколькими способами могут быть распределены первые три места.

6. 6 туристов желает остановиться в гостинице, в которой 7 свободных номеров. Сколькими способами их можно расселить, если 4 желают жить в отдельных номерах и 2 в одном номере.

7. В лифте едут 4 человека. При этом каждый может сойти на любом из 5 этажей. Сколько различных комбинаций выхода из лифта имеется.

8. В вагоне имеется 6 свободных мест по ходу движения и 5 –против хода. Вошли 5 пассажиров. Из них 3 желают ехать по ходу движения, 2-против хода. Сколькими способами они могут разместиться.

9. Одновременно подбрасываются две монеты. Перечислите все возможные исходы. Какова вероятность выпадения двух гербов? Герба и решки?

10. Подбрасываются три монеты. Какова вероятность выпадения трех гербов? Герба и двух решек? Хотя бы одного герба?

11. Игральная кость подбрасывается один раз. Какова вероятность того, что число выпавших очков кратно трем?

12. Подбрасываются две игральные кости. Найти вероятность того, что число выпавших очков больше двух.

13. Подбрасываются две игральные кости. Найти вероятность того, что число выпавших очков равно семи.

14. Подбрасываются две игральные кости. Найти вероятность того, что сумма выпавших очков равна пяти, а произведение четырем.

15. Подбрасываются две игральные кости. Найти вероятность того, что произведение выпавших очков равно шести.

16. На шести карточках написаны буквы У, Т, Ф, Б, Л, О. Карточки перемешивают, берут по одной и кладут последовательно рядом. Какова вероятность того, что получится слово ФУТБОЛ?

17. На каждой из шести одинаковых карточек напечатана одна из следующих букв: В, М, Ч, Р, А, Т. Карточки перемешивают. Найти вероятность того, что на четырех вынутых по одной и расположенных слева направо карточках можно прочесть слово ВРАЧ.

18. Фотограф располагает в ряд одного мальчика и двух девочек случайным образом. Какова вероятность того, что на фотографии девочки и мальчики будут чередоваться?

19. В клетке 40 мышей, из них 12 белых. Найти вероятность того, что среди извлеченных четырех мышей половина белых.

20. В группе студентов 7 юношей и 5 девушек. Для дежурства отобраны шесть человек. Какова вероятность того, что среди отобранных окажутся четверо юношей?

21. Из партии в 1000 деталей контролер отобрал для проверки 50. Найти вероятность того, что среди отобранных деталей не окажется бракованных, если во всей партии их четыре.

22. Из шести карточек с буквами Л, И, Т, Е, Р, А наудачу выбирают последовательно четыре. Какова вероятность того, что при этом получится слово ТИРЕ?

23. Набирая номер телефона, абонент забыл последние три цифры, и помня лишь, что эта цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.

24. В фирме работают 6 мужчин и 4 женщины. По табельным номерам наудачу отобраны 7 человек. Найти вероятность того, что средиотобранных лиц окажутся 3 женщины.

25. Собрание, на котором присутствует 25 человек, в том числе 5 женщин, выбирает делегацию из 3 человек. Считая, что каждый из присутствующих с одинаковой вероятностью может быть избран, найти вероятность того, что в делегацию войдут 2 женщины и 1 мужчина.

26. На полке расставляют наудачу 7 книг. Найти вероятность того, что 2 определенные книги окажутся рядом.

27. Бросают 3 игральные кости. Найти вероятность того, что на всех выпадет одинаковое число очков.

28. В группе 12 студентов, среда которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов 5 отличников.

29. Группа из 10 мужчин и 10 женщин делится случайным образом на две равные части. Найти вероятность того, что в каждой части мужчин и женщин одинаково.

30. В комнате 15 мест. Найти вероятность того, что из 10 человек 5 займут определенные места, если места занимаются ими случайным образом.

31. Для производственной практики на 30 студентов предоставлено 15 мест в Рязани, 8 - в Тамбове и 7 - в Воронеже. Какова вероятность того, что два определенных студента попадут на практику в одни город?

32. Брошены три одинаковых игральных кости. Найти вероятность того, что цифра 6 появится хотя бы на одной грани.

33. В партии из 10 изделий имеется 4 бракованных. Наугад выбирают 5 из­делий. Определить вероятность того, что среди этих 5 изделий окажется 3 брако­ванных.

34. Три стрелка стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75; для второго - 0,8; для третьего - 0,9. Найти вероятность того, что: а) все три стрелка попадут в цель; б) только одни стрелок попадет в цель.

35. В ремонтной мастерской имеются 8 мастеров, из которых 5 высшей категории и 3 первой. Для выполнения задания случайно отобрали 4 мастера. Какая вероятность, что среди них 2 высшей категории?

36. Из коробки, в которой 20 деталей без дефектов в 5 с дефектами, 6ерут наудачу 3 детали. Чему равна вероятность того, что, по крайней мере, одна деталь без дефекта?

37. Слово «карета», составленное из букв-кубиков, рассыпано на отдельные буквы, которые затем сложены в коробке. Из коробки наугад извлекают буквы одну за другой. Какова вероятность получить при таком извлечении слово «ракета»?

38. Производится стрельба по мишени. Вероятность попадания при одном выстреле 0,7. Найти вероятность того, что по мишени будет произведено не менее трех выстрелов, если после первого попадания стрельба прекращается.

39. В гостинице имеется 7 свободных номеров. В нее собирается поселиться 2 человека. Какая вероятность, что они будут жить в соседних номерах, если их номера выбираются случайно.

40. Ящик содержит 10 деталей, среди которых 3 стандартных. Найти вероятность того, что из наудачу отобранных 5 деталей окажется не более одной стандартной.

41. Брошены две одинаковых игральных кости. Найти вероятность того, что цифра 6 появится хотя бы на одной грани.

42. Для поражения цели достаточно попадания хотя бы одного снаряда. Произведено два залпа из двух орудий. Найти вероятность поражения цели, если вероятность попадания в цель при одном выстреле из первого орудия равна 0,3, а из второго - 0,4.

43. В урне лежит 12 белых и 8 красных шаров. Вынули 8 шаров. Какова вероятность того, что три из них красные?

44. В экономическом отделе фирмы 7 менеджеров и 5 финансистов. Для выполнения задания были отобраны 4 человека. Какая вероятность, что среди них 3 менеджера?