Схема выбора с возвращением.
Если при выборке 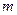 элементов из
элементов из 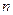 элементы возвращаются обратно и упорядочиваются, то говорят, что это размещения с повторениями.
элементы возвращаются обратно и упорядочиваются, то говорят, что это размещения с повторениями.
Вычисляются по формуле
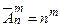 .
.
Пример 10. Сколько пятизначных чисел можно составить, используя цифры 2, 5, 7, 8?
Решение. Все пятизначные числа, составленные из заданных цифр, могут отличаться либо порядком их следования, либо самими цифрами, следовательно, они являются размещениями из 4-х элементов по 5 с повторениями.
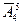 = 45= 1024 (этот результат можно получить, используя правило умножения).
= 45= 1024 (этот результат можно получить, используя правило умножения).
Если при выборке 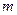 элементов из
элементов из 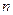 элементов множества элементы возвращаются, но не упорядочиваются, то говорят, что это сочетания с повторениями.
элементов множества элементы возвращаются, но не упорядочиваются, то говорят, что это сочетания с повторениями.
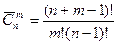 .
.
Пример 11. Сколькими способами можно составить букет из 5 цветов, если в наличии есть цветы трех сортов?
Решение. Рассматриваемое множество состоит из трех различных элементов, а выборки имеют объем, равный 5. Поскольку порядок расположения цветов в букете не играет роли, то искомое число букетов равно числу сочетаний с повторениями из трех элементов по 5 в каждом. По формуле имеем
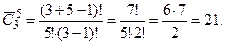
Пусть во множестве из 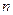 элементов есть
элементов есть 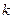 различных элементов, при этом 1-ый элемент повторяется
различных элементов, при этом 1-ый элемент повторяется 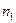 раз, второй элемент –
раз, второй элемент – 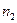 раз,…,
раз,…, 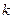 -тый элемент –
-тый элемент –  раз, причем
раз, причем  . Перестановки из
. Перестановки из 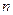 элементов данного множества называют перестановками с повторениями из
элементов данного множества называют перестановками с повторениями из 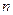 элементов
элементов
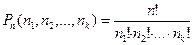
Пример 12. Сколько различных пятизначных чисел можно составить из цифр 3,3,5,5,8?
Решение. Всего элементов 5 ( 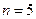 ).
).
Первый элемент 3 повторяется 2 раза, следовательно,
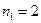 .
.
Второй элемент 5 повторяется 2 раза, 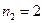
Третий элемент 8 повторяется 1 раз, 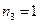
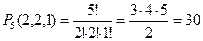
Дата добавления: 2016-09-06; просмотров: 4348;











