Схема выбора без возвращений

Рассмотрим множество, состоящее из 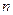различных элементов.

Соединения, отличающиеся друг от друга составом элементов или их порядком, каждое из которых содержит 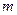элементов взятых из 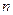элементов, называются размещениями.

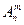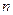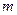Обозначаются . Читается – число размещений, взятых из по , вычисляется по формуле

,

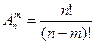где 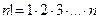(факториал), 1! = 1, 0! = 1.

Пример 6. Сколько трехзначных чисел можно составить из чисел 1,2,3,4,5, если цифры не повторяются?

Решение. 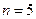, 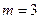. Получаемые соединения должны отличаться составом элементов и их порядком, следовательно, используем формулу размещений:

.

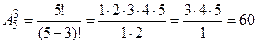Соединения, отличающиеся друг от друга, по крайней мере одним элементом, каждое из которых содержит 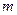элементов взятых из 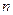элементов, называются сочетаниями. (Порядок элементов роли не играет)

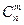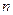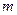Обозначается , читается – число сочетаний из по , вычисляется по формуле

.

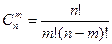Пример 7. В бригаде из 25 человек нужно выбрать 4-х для работы на определенном участке. Сколькими способами это можно сделать?

Решение.

Необходимо выбрать 4 элемента из 25 возможных, причем порядок выбора не важен, следовательно, используем формулу сочетаний:

.

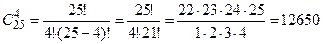Соединения, каждое из которых содержит 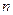различных элементов, взятых в определенном порядке, называются перестановками. (Рассматриваются все 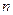элементов, отличаются только порядком)

Вычисляются по формуле

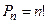
Пример 8. Сколькими способами можно расставить 6 различных книг на одной полке?

Решение. .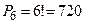

Пример 9. Сколькими способами можно выбрать 3 цветка из вазы, в которой стоят 10 красных и 4 розовых гвоздики? А если выбрать 1 красную гвоздику и 2 розовых?

Решение.

1) Т.к. порядок выбора цветов не имеет значения, то выбрать 3 цветка из вазы можно 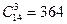способами.

2) Выбрать 2 розовые гвоздики из имеющихся можно 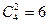способами, одну красную из имеющихся 10 можно выбрать 10 способами. По правилу умножения букет из одной красной и 2-х розовых гвоздик можно составить 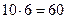способами.