ОСНОВЫ ТЕОРИИ ГИДРОДИНАМИЧЕСКИХ СОПРОТИВЛЕНИЙ
Движение реальных жидкостей внутри каналов и труб сопровождается уменьшением механической энергии потока из-за действия сил сопротивления различной природы и характеризуется величиной потери давления на рассматриваемом участке потока.
Потери по длине 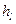 , с учетом формулы Дарси-Вейсбаха можно выразить:
, с учетом формулы Дарси-Вейсбаха можно выразить:
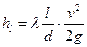 ,
, 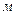 (9.2)
(9.2)
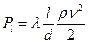 ,
, 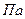 (9.3)
(9.3)
где 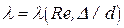 - безразмерный параметр, характеризующий потери на трение по длине и по этой причине в специальной литературе его принято называть коэффициентом гидравлического трения.Этот коэффициент зависит от числа Рейнольдса и безразмерного параметра
- безразмерный параметр, характеризующий потери на трение по длине и по этой причине в специальной литературе его принято называть коэффициентом гидравлического трения.Этот коэффициент зависит от числа Рейнольдса и безразмерного параметра 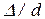 , называемого относительной шероховатостью. Абсолютная шероховатость D,
, называемого относительной шероховатостью. Абсолютная шероховатость D, 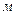 находится по справочной литературе и зависит от вида материала стенок каналов и трубопроводов, а также от срока эксплуатации. Как правило, функциональную зависимость
находится по справочной литературе и зависит от вида материала стенок каналов и трубопроводов, а также от срока эксплуатации. Как правило, функциональную зависимость 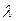 от числа Рейнольдса и относительной шероховатости определяют эмпирическим или полуэмпирическим путем, но в некоторых простых случаях, например, при установившемся ламинарном течении в гладких трубах коэффициент
от числа Рейнольдса и относительной шероховатости определяют эмпирическим или полуэмпирическим путем, но в некоторых простых случаях, например, при установившемся ламинарном течении в гладких трубах коэффициент 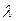 может быть получен аналитическим методом. Из формулы (9.3) следует, что потери на трение возрастают со средней скоростью движения жидкости и длиной участка, и обратно пропорциональны диаметру трубопровода.
может быть получен аналитическим методом. Из формулы (9.3) следует, что потери на трение возрастают со средней скоростью движения жидкости и длиной участка, и обратно пропорциональны диаметру трубопровода.
Формула Дарси-Вейсбаха справедлива для любых режимов течения как ламинарного, так и турбулентного. В этом смысле она является универсальной. Различие состоит лишь в форме функциональной зависимости 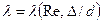 , которая соответственно отличается для ламинарного и турбулентного режимов:
, которая соответственно отличается для ламинарного и турбулентного режимов:
- если режим движения жидкости ламинарный, то коэффициентом гидравлического трения 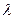 можно найти по формуле Пуазейля:
можно найти по формуле Пуазейля:
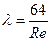 ;(9.4)
;(9.4)
- коэффициент 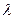 , вычисленный для турбулентного течения в гладких круглых трубах по формуле Блазиуса
, вычисленный для турбулентного течения в гладких круглых трубах по формуле Блазиуса
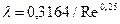 ; (9.5)
; (9.5)
- большая область гидродинамических течений укладываются в формулу Альтшуля, которая распространяется на область переходного и части турбулентного режима.
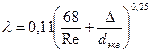 ; (9.6)
; (9.6)
Дата добавления: 2016-05-26; просмотров: 1279;











