Краткие сведения из теории вероятностей

<456 7 8 9 10 >

Теория вероятности оперирует с событиями, которые обозначаются большими буквами латинского алфавита: 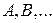События могут произойти или не произойти случайным образом. Среди событий выделяют два особых события: достоверное событие 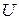, которое происходит всегда, и невозможное событие 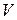, которое не происходит никогда. Событие 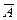называется противоположным 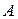, оно происходит тогда, когда 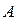не происходит. Событие, состоящее в наступлении обоих событи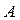й и 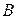, называется произведением событий и обозначается как 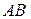или 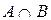. Событие, состоящее в наступлении хотя бы одного события, называется суммой событий и обозначается 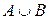. Наступление события 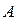при условии, что наступило событие 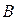,обозначают как .

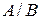Из определений следует, что .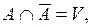

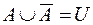Каждому случайному событию ставится в соответствие неотрицательное число 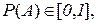которое называется вероятностью события.

Справедливы следующие законы теории вероятностей.

· ;

· ;

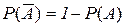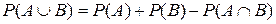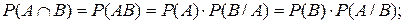· (2.5)

· .

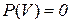· Событие 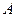не зависит от события ,

есл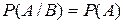и и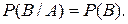

Поэтому для независимых событи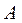й и 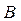имеем .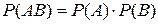

Выведем теперь формулу, которая потребуется в дальнейшем. Из формулы (2.5) для вероятности произведения событий 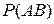следует

, ,

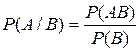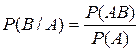Откуда

.

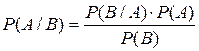Вероятность 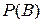формально можно представить в виде

,

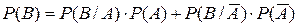В результате получаем так называемую формулу Байеса:

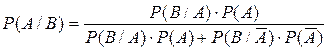. (2.6)

Эта формула широко применяется в системах поддержки принятия решений, поскольку с ее помощью можно уточнять и накапливать информацию в процессе функционирования системы.

Предположим, что имеется некоторая гипотеза 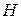и априорная вероятность того, что эта гипотеза истинна 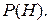Пусть, далее, имеется свидетельство 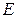в пользу этой гипотезы. Это позволит уточнить вероятность истинности гипотезы . По формуле Байеса (3) имеем:

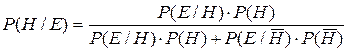. (2.7)

Пример. Предположим, что ЛПР сомневается в справедливости гипотезы 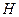и оценивает вероятность того, что она справедлива, величиной 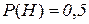и, соответственно, что она ложна, вероятностью 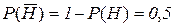. Однако привлеченный эксперт 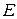считает вероятность того, что гипотеза верна, равной 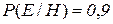, а вероятность ошибки он оценивает величиной 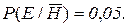В результате расчета по формуле Байеса (4) получим

.

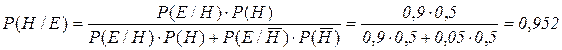Таким образом, ЛПР может изменить свою оценку вероятности гипотезы .

<456 7 8 9 10 >

Дата добавления: 2016-09-06; просмотров: 1219;