Структура базы знаний и алгоритм логического вывода
Мы рассмотрим упрощенный вариант архитектуры экспертной системы (ЭС), предложенной К. Нейлором и базирующейся на использовании алгоритмов Байеса, [22, 34] .
База знаний диагностирующей ЭС содержит записи двух типов:
· формат 1:знания о конкретных гипотезах (диагнозах) – 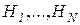 ;
;
· формат 2: знания о свидетельствах (фактах) – 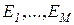 .
.
Запись, описывающая конкретную гипотезу 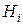 в формате 1, имеет следующую структуру:
в формате 1, имеет следующую структуру:
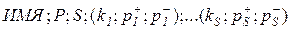 . (2.8)
. (2.8)
Здесь:
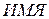 - название гипотезы
- название гипотезы 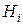 ;
;
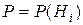 - априорная вероятность данной гипотезы;
- априорная вероятность данной гипотезы;
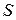 - число свидетельств (фактов) для данной гипотезы;
- число свидетельств (фактов) для данной гипотезы;
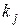 - номер свидетельства;
- номер свидетельства;
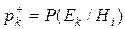 - вероятность выполнения свидетельства
- вероятность выполнения свидетельства 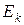 , если гипотеза
, если гипотеза 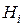 верна;
верна;
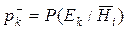 - вероятность выполнения свидетельства,
- вероятность выполнения свидетельства, 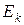 если гипотеза
если гипотеза 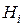 не верна;
не верна; 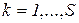 .
.
Знания о свидетельствах (фактах) 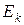 должны быть представлены в формате 2 в следующем виде:
должны быть представлены в формате 2 в следующем виде:
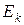 - номер свидетельства; Название свидетельства; Задаваемый вопрос.
- номер свидетельства; Название свидетельства; Задаваемый вопрос.
|
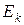 по формуле:
по формуле:
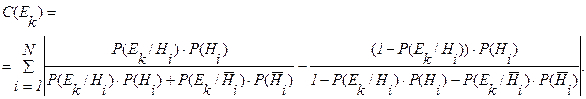
Здесь 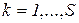 - номера свидетельств
- номера свидетельств 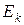 , указанных в формате 2;
, указанных в формате 2; 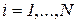 - номера гипотез
- номера гипотез 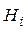 , указанных в формате 1, для подтверждения которых требуется свидетельство
, указанных в формате 1, для подтверждения которых требуется свидетельство 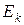 .
.
Величина 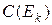 определяет полную сумму максимально возможных изменений вероятностей по всем
определяет полную сумму максимально возможных изменений вероятностей по всем 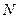 гипотезам, имеющимся в базе данных за счет свидетельства
гипотезам, имеющимся в базе данных за счет свидетельства 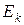 .
.
Алгоритм логического вывода состоит из следующих шагов.
1. Вычисляем все 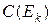 ,
, 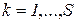 , выбираем свидетельство
, выбираем свидетельство 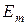 с наибольшей оценкой:
с наибольшей оценкой: 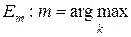
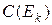 .
.
2. Задаем пользователю вопрос, хранящийся в формате 2 выбранного свидетельства.
Ответ может быть: да, нет, не знаю.
3. В зависимости от ответа пересчитываем вероятности всех гипотез, связанных со свидетельством 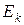 . Пересчет производится по формуле Байеса.
. Пересчет производится по формуле Байеса.
В случае ответа да:
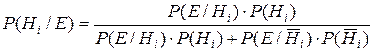 ; (2.10)
; (2.10)
в случае ответа нет:
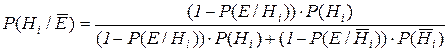 ; (2.11)
; (2.11)
в случае ответа не знаю:
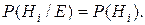 (2.12)
(2.12)
4. После этого заменяем в массиве записей о гипотезах (5) вероятности 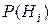 на
на 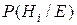 ,
, 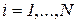 .
.
5. Повторяем описанную процедуру (пункты 1–4) для всех свидетельств. Свидетельство, по которому уже был задан вопрос, в дальнейшем диалоге не участвует, его цена обнуляется.
6. После опроса всех свидетельств получаем окончательные значения вероятностей гипотез, это и является окончательным диагнозом.
Пример. Вернемся к задаче о диагностике состояния автомобиля и рассмотрим ее на основе изложенной выше теории.
Формат 1
Гипотезы 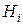 :
:
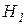 : Сел аккумулятор;
: Сел аккумулятор;
0,1; 5; (1; 0; 0,99); (2; 0,7; 0,05); (4; 0,2; 0,5); (5; 0; 0,99); (6; 1; 0,01)
 : Нет бензина; 0,05; 2; (2; 1; 0,01); (6; 0,9; 0,02)
: Нет бензина; 0,05; 2; (2; 1; 0,01); (6; 0,9; 0,02)
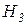 : Отсырел распределитель зажигания; 0,01; 3; (3; 0,9; 0,1); (4; 0,25; 0,5); (6; 0,9; 0,02)
: Отсырел распределитель зажигания; 0,01; 3; (3; 0,9; 0,1); (4; 0,25; 0,5); (6; 0,9; 0,02)
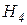 : Загрязнены свечи; 0,01; 2; (4; 0,01; 0,5); (6; 0,9; 0,02)
: Загрязнены свечи; 0,01; 2; (4; 0,01; 0,5); (6; 0,9; 0,02)
Формат 2
Свидетельства (симптомы) 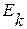 и вопросы к пользователю
и вопросы к пользователю
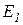 Фары горят; Горят ли фары?
Фары горят; Горят ли фары?
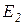 Указатель бензина на нуле; Есть ли бензин?
Указатель бензина на нуле; Есть ли бензин?
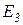 Автомобиль отсырел; Не находился ли автомобиль долго под дождем?
Автомобиль отсырел; Не находился ли автомобиль долго под дождем?
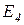 Автомобиль недавно прошел техобслуживание; Проходил ли автомобиль недавно техобслуживание?
Автомобиль недавно прошел техобслуживание; Проходил ли автомобиль недавно техобслуживание?
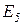 Стартер крутится; Крутится ли стартер?
Стартер крутится; Крутится ли стартер?
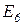 Автомобиль не заводится; Автомобиль не заводится?
Автомобиль не заводится; Автомобиль не заводится?
По данной базе знаний и формуле (2.9) можно сформировать массив 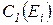 исходных цен свидетельств (таблица 2.4), а также вероятности гипотез
исходных цен свидетельств (таблица 2.4), а также вероятности гипотез 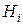 (таблица 2.5) на каждом шаге процедуры принятия решений.
(таблица 2.5) на каждом шаге процедуры принятия решений.
Таблица 2.4
Цены свидетельств 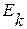
Свидетельства
(симптомы) 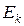
| Гипотезы
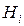
| 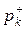
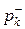
| Шаг 1
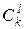
| Шаг 2

| Шаг 3

| Шаг 4
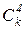
| Шаг 5
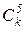
|
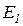 Фары горят Фары горят
| 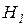
| 0,917 | 0,999 | 0,999 | |||
| 0,99 | |||||||
 Указатель бензина на нуле Указатель бензина на нуле
| 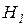
| 0,7 | 1,415 | 1,213 | |||
| 0,05 | |||||||
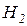
| |||||||
| 0,01 | |||||||
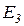 Автомобиль отсырел Автомобиль отсырел
| 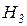
| 0,9 | 0,082 | 0,755 | 0,755 | 0,755 | |
| 0,1 | |||||||
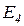 Автомобиль недавно прошел техобслуживание Автомобиль недавно прошел техобслуживание
| 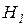
| 0,2 | 0,137 | 0,815 | 0,597 | 0,597 | |
| 0,5 | |||||||
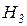
| 0,25 | ||||||
| 0,5 | |||||||
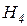
| 0,01 | ||||||
| 0,5 | |||||||
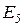 Стартер крутится Стартер крутится
| 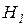
| 0,917 | 0,999 | 1,000 | |||
| 0,99 | |||||||
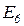 Автомобиль не заводится Автомобиль не заводится
| 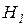
| 2,238 | |||||
| 0,01 | |||||||
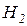
| 0,9 | ||||||
| 0,02 | |||||||
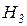
| 0,9 | ||||||
| 0,02 | |||||||
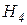
| 0,9 | ||||||
| 0,02 |
Таблица 2.5
Вероятности гипотез
| Гипотеза | Шаг 0 | Шаг 1 | Шаг 2 | Шаг 3 | Шаг 4 | Шаг 5 |
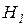 : Сел аккумулятор : Сел аккумулятор
| 0,1 | 0,917 | 0,994 | |||
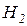 : Есть ли бензин : Есть ли бензин
| 0,05 | 0,703 | 0,959 | 1,0 | 1,0 | 1,0 |
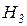 : Отсырел распре-делитель зажигания : Отсырел распре-делитель зажигания
| 0,01 | 0,312 | 0,312 | 0,312 | 0,312 | 0,330 |
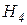 :Загрязнены свечи :Загрязнены свечи
| 0,01 | 0,312 | 0,312 | 0,312 | 0, 312 | 0,327 |
По исходным вероятностям (Шаг 0) рассчитываются цены свидетельств и начинается диалог с системой. Свидетельства с наибольшей ценой выделены.
Шаг 1. Наибольшую цену имеет свидетельство 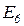 : Автомобиль не заводится. Задается вопрос: Автомобиль не заводится? При ответе ДА пересчитываются вероятности гипотез и цены свидетельств.
: Автомобиль не заводится. Задается вопрос: Автомобиль не заводится? При ответе ДА пересчитываются вероятности гипотез и цены свидетельств.
Шаг 2. Наибольшую цену имеет свидетельство  : Указатель бензина на нуле. Задается вопрос: Есть ли бензин? При ответе ДА пересчитываются вероятности гипотез и цены свидетельств.
: Указатель бензина на нуле. Задается вопрос: Есть ли бензин? При ответе ДА пересчитываются вероятности гипотез и цены свидетельств.
Шаг 3. Наибольшую цену имеет свидетельство 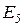 : Стартер крутится. Задается вопрос: Крутится ли стартер? При ответе ДА пересчитываются вероятности гипотез и цены свидетельств.
: Стартер крутится. Задается вопрос: Крутится ли стартер? При ответе ДА пересчитываются вероятности гипотез и цены свидетельств.
Шаг 4. Наибольшую цену имеет свидетельство 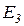 : Автомобиль отсырел. Задается вопрос: Не находился ли автомобиль долго под дождем? При ответе НЕ ЗНАЮ вероятности не изменяются.
: Автомобиль отсырел. Задается вопрос: Не находился ли автомобиль долго под дождем? При ответе НЕ ЗНАЮ вероятности не изменяются.
Шаг 5. Единственное свидетельство с ненулевой ценой 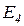 : Автомобиль недавно прошел техобслуживание. При ответе НЕТ изменяются вероятности гипотез
: Автомобиль недавно прошел техобслуживание. При ответе НЕТ изменяются вероятности гипотез 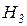 и
и 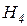 .
.
Диагноз:Гипотеза 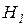 отвергается, поскольку
отвергается, поскольку 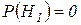 . Это говорит о том, что аккумулятор в порядке.
. Это говорит о том, что аккумулятор в порядке.
Гипотеза 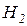 подтверждается, поскольку
подтверждается, поскольку 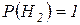 . Это говорит о том, что бензин имеется.
. Это говорит о том, что бензин имеется.
Гипотеза 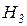 имеет вероятность
имеет вероятность 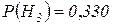 , поскольку неизвестно, был ли автомобиль под дождем.
, поскольку неизвестно, был ли автомобиль под дождем.
Гипотеза 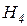 имеет вероятность
имеет вероятность  , поскольку автомобиль не прошел техобслуживание и неизвестно, был ли он под дождем.
, поскольку автомобиль не прошел техобслуживание и неизвестно, был ли он под дождем.
Вопросы и задания для самостоятельного изучения
1. Составьте когнитивную карту какой-либо знакомой Вам деятельности, например, успехов в спорте, в учебе, в научной работе и др.
2. Выберите знакомую Вам область и проранжируйте входящие в нее объекты (например, марки автомобилей, футбольные команды, изучаемые Вами дисциплины и др.). Сравните ранжировки, полученные по методу средних арифметических и по методу медиан.
3. Для знакомой Вам области составьте продукционную систему, позволяющую выбрать одну из гипотез (например, Крис Нейлор [22] иллюстрирует создание продукционной системы на примере выбора между птицей и самолетом).
4. Ниже приводится фрагмент медицинской экспертной системы, позволяющий отличить грипп от простуды.
Формат 1
Структура описания гипотезы
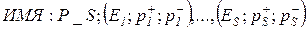
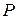 - априорная вероятность гипотезы,
- априорная вероятность гипотезы,
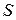 - количество свидетельств (симптомов),
- количество свидетельств (симптомов),
 - имя симптома,
- имя симптома, 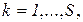
 - вероятность выполнения свидетельства для данной гипотезы,
- вероятность выполнения свидетельства для данной гипотезы,
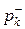 - вероятность выполнения свидетельства при неверности данной гипотезы.
- вероятность выполнения свидетельства при неверности данной гипотезы.
Гипотезы 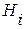

Формат 2
Свидетельства (симптомы) 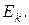
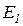 : Чихание. Вы часто чихаете?
: Чихание. Вы часто чихаете?
 : Слезы из глаз. Слезятся ли у вас глаза?
: Слезы из глаз. Слезятся ли у вас глаза?
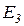 : Боль в горле. Болит ли у вас горло?
: Боль в горле. Болит ли у вас горло?
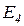 : Насморк. Есть ли у вас насморк?
: Насморк. Есть ли у вас насморк?
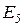 : Головная боль. Болит ли у вас голова?
: Головная боль. Болит ли у вас голова?
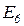 : Высокая температура. Ваша температура выше 37 градусов?
: Высокая температура. Ваша температура выше 37 градусов?
На основе алгоритма, приведенного в п. 2.4.3 и собственного опыта, задавая системе вопросы, оцените вероятности гипотез 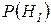 и
и 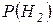 .
.
Глава 3 Методы оптимизации в задачах
принятия решений
Как отмечалось ранее, принятие решений часто связано с учетом множества противоречивых требований, удовлетворить которым одновременно в полной мере невозможно. Математически такая ситуация приводит к задачам, которые получили название задач многокритериальной оптимизации.
Общая постановка детерминированной многокритериальной задачи параметрической оптимизации с ограничениями формулируется следующим образом [34]:
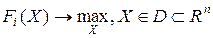 ,
, 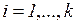 . (3.1)
. (3.1)
В этой формуле 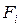 ,
, 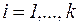 представляют собой численные критерии, оценивающие качество решения. Множество
представляют собой численные критерии, оценивающие качество решения. Множество 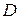 называется множеством допустимых решений. В пределах этого множества может задаваться ряд ограничений на вектор
называется множеством допустимых решений. В пределах этого множества может задаваться ряд ограничений на вектор 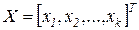 :
:
· прямые (интервальные) ограничения
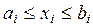 ,
, 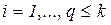 ; (3.2а)
; (3.2а)
· функциональные ограничения
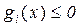 ,
, 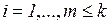 , (3.2б)
, (3.2б)
где 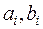 - заданные числа,
- заданные числа, 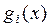 – заданные функции.
– заданные функции.
Предполагается, что каждый из критериальных параметров 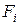 необходимо максимизировать. Это не ограничивает общности, так как минимизация функции
необходимо максимизировать. Это не ограничивает общности, так как минимизация функции 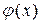 эквивалентна максимизации
эквивалентна максимизации 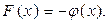 Аналогично, замена знака у левой части неравенства
Аналогично, замена знака у левой части неравенства 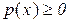 меняет знаки неравенств на противоположные и приводит их к виду
меняет знаки неравенств на противоположные и приводит их к виду 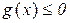 .
.
В том случае, когда критерий всего один 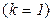 , получается классическая задача однокритериальной оптимизации. Такие задачи мы и рассмотрим в первую очередь.
, получается классическая задача однокритериальной оптимизации. Такие задачи мы и рассмотрим в первую очередь.
Ниже, в основном, пойдет речь о постановках задач оптимизации. Что касается численных алгоритмов решения таких задач, то мы, за исключением некоторых простых случаев, их не приводим, полагая, во-первых, что численные методы изучены ранее в курсах прикладной математики, а во-вторых, что эти методы доступны в математических пакетах и сети Интернет.
3.1 Принятие решений на основе методов линейного программирования
Среди оптимизационных задач в теории принятия решений наиболее известны задачи линейного программирования, в которых максимизируемая функция 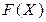 в выражении (3.1) является линейной, а ограничения
в выражении (3.1) является линейной, а ограничения 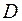 задаются линейными неравенствами [34, 37].
задаются линейными неравенствами [34, 37].
Базовая формулировка задачи линейного программирования выглядит следующим образом.
Исходная задача.
В простейшем виде задача линейного программирования формулируется следующим образом.
Имеется  неизвестных величин
неизвестных величин 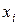 ,
, 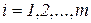 , которые образуют вектор – столбец
, которые образуют вектор – столбец 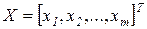 .
.
Значок 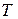 здесь и далее означает транспонирование матицы.
здесь и далее означает транспонирование матицы.
Компоненты вектора 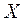 подчиняются ограничениям
подчиняются ограничениям
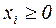 ,
, 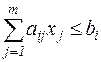
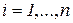 . (3.3)
. (3.3)
Величины 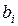 также могут быть представлены в виде вектора-столбца
также могут быть представлены в виде вектора-столбца 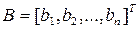 , а коэффициенты
, а коэффициенты 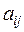 ,
, 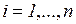 ,
, 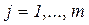 образуют
образуют 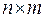 ‑ матрицу
‑ матрицу 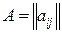 .
.
С учетом введенных обозначений неравенство (3.3) можно представить в матричном виде:
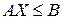 . (3.4)
. (3.4)
Каждая величина 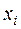 имеет «цену»
имеет «цену» 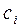 ,
, 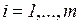 . Тогда общая цена всех неизвестных
. Тогда общая цена всех неизвестных 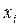 составит
составит
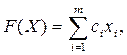 (3.5)
(3.5)
или в матричной записи
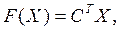 (3.6)
(3.6)
где 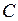 - m-вектор-столбец
- m-вектор-столбец
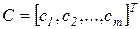 . (3.7)
. (3.7)
Задача линейного программирования заключается в следующем.
· Заданы матрица 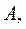 векторы
векторы 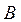 и
и 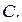
· Принятие решения заключается в нахождении такого вектора 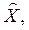 который удовлетворяет ограничениям (3.4) и обеспечивает максимум выражения (3.5). Формально это условие может быть записано в виде
который удовлетворяет ограничениям (3.4) и обеспечивает максимум выражения (3.5). Формально это условие может быть записано в виде
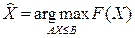 . (3.8)
. (3.8)
Двойственная задача. Каждой задаче линейного программирования соответствует так называемая двойственная задача. В ней в качестве неизвестного появляется вектор двойственных переменных 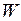 размерностью
размерностью 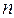 . Матрица ограничений
. Матрица ограничений 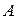 транспонируется по сравнению с исходной задачей, т.е. строки переходят в столбцы, и наоборот. Неравенства в ограничениях меняют знак, то есть вместо максимума ищется минимум (или наоборот, вместо минимума – максимум). Задача, двойственная к двойственной, – это сама исходная задача.
транспонируется по сравнению с исходной задачей, т.е. строки переходят в столбцы, и наоборот. Неравенства в ограничениях меняют знак, то есть вместо максимума ищется минимум (или наоборот, вместо минимума – максимум). Задача, двойственная к двойственной, – это сама исходная задача.
Сравним исходную задачу и двойственную к ней.
Исходная задача:
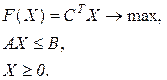
Двойственная задача:
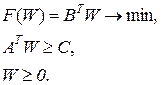
Почему двойственная задача столь важна? Дело в том, что оптимальные значения 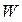 показывают стоимость материала и труда соответственно, если их оценивать по вкладу в целевую функцию. При этом оптимальные значения целевых функций в исходной и двойственной задачах совпадают (т.е. максимум в исходной задаче совпадает с минимумом в двойственной). Поэтому их называют «объективно обусловленными оценками» сырья и рабочей силы.
показывают стоимость материала и труда соответственно, если их оценивать по вкладу в целевую функцию. При этом оптимальные значения целевых функций в исходной и двойственной задачах совпадают (т.е. максимум в исходной задаче совпадает с минимумом в двойственной). Поэтому их называют «объективно обусловленными оценками» сырья и рабочей силы.
Методы решения сформулированных задач хорошо разработаны и реализованы практически во всех математических пакетах программ, например, в Exel. Наиболее часто используется так называемый симплекс-метод решения задач линейного программирования. Мы не будем останавливаться на изложении этих методов, а сосредоточимся на рассмотрении примеров конкретных постановок для принятия решений.
3.2 Математическая модель планирования производства
Рассмотренная ниже модель предназначена для принятия решения об оптимизации плана выпуска различных видов продукции из имеющихся нескольких видов сырья [10]. Такие задачи возникают в нефтепереработке, пищевой промышленности, при раскрое плит на заготовки, или круглого леса на пиломатериалы, а также в других областях.
Имеется 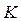 видов сырья, из которого нужно изготовить
видов сырья, из которого нужно изготовить 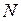 видов продукции. Каждый из видов сырья может быть использован различным способом в соответствии с технологическими картами, которые мы будем считать заданными. Обозначим
видов продукции. Каждый из видов сырья может быть использован различным способом в соответствии с технологическими картами, которые мы будем считать заданными. Обозначим 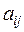 объем
объем 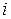 -й продукции при обработке сырья j-м способом (
-й продукции при обработке сырья j-м способом ( 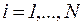 ;
; 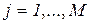 ). Здесь
). Здесь 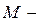 общее количество технологических карт. Эти величина образуют
общее количество технологических карт. Эти величина образуют 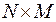 матрицу
матрицу 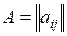 , в которой каждая строка соответствует одному виду продукции, а каждый столбец – технологической карте.
, в которой каждая строка соответствует одному виду продукции, а каждый столбец – технологической карте.
Карты пронумерованы все подряд, но каждая карта пригодна для обработки только определенного вида сырья. Этот факт может быть описан с помощью переменных 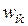 , которые принимают значение 1, если
, которые принимают значение 1, если 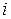 -я карта может быть использована для обработки сырья
-я карта может быть использована для обработки сырья 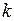 -го вида, и значение 0 в противном случае (
-го вида, и значение 0 в противном случае ( 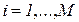 ;
; 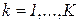 ). Переменные
). Переменные 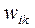 образуют
образуют 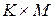 ‑ матрицу
‑ матрицу 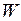 , состоящую из нулей и единиц следующего вида:
, состоящую из нулей и единиц следующего вида:
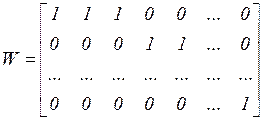 . (3.9)
. (3.9)
В этой матрице каждая строка соответствует одному виду сырья, а каждый столбец – одной технологической карте.
Принятие решения в данной задаче состоит в определении интенсивности использования способов производства продукции, т.е. технологических карт. Обозначим 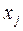 количество сырья, обработанного при использовании
количество сырья, обработанного при использовании 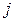 -й технологической карты. Эти величины образуют вектор-столбец
-й технологической карты. Эти величины образуют вектор-столбец 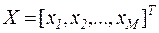 , который называют планом производства. Если план производства задан, то количество произведенной продукции
, который называют планом производства. Если план производства задан, то количество произведенной продукции 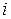 -го вида
-го вида 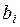 вычисляется по формуле
вычисляется по формуле
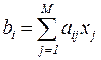 . (3.10)
. (3.10)
Всю спецификацию вырабатываемой продукции можно представить в виде вектора-столбца 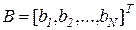 , который может быть представлен как произведение матрицы
, который может быть представлен как произведение матрицы 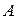 на вектор
на вектор 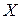 :
:
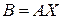 . (3.11)
. (3.11)
Общий объем (или стоимость) продукции, производимой при плане производства 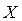 ,определится путем сложения объемов по всем ее видам:
,определится путем сложения объемов по всем ее видам:
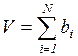 . (3.12)
. (3.12)
С учетом (2.13), изменяя порядок суммирования, получим:
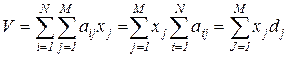 . (3.13)
. (3.13)
В этой формуле 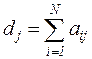 - общий объем (или стоимость) продукции всех видов, получаемой из единицы сырья при использовании в производстве
- общий объем (или стоимость) продукции всех видов, получаемой из единицы сырья при использовании в производстве 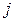 ‑й технологической карты. Эти величины также могут быть объединены в вектор-столбец размерностью M:
‑й технологической карты. Эти величины также могут быть объединены в вектор-столбец размерностью M: 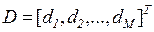 .
.
Получим более компактную запись для общего объема продукции:
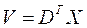 .
.  (3.14)
(3.14)
Обратимся теперь к сырью. Пусть 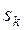 (
( 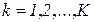 ) - количество сырья
) - количество сырья 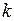 ‑го вида, идущего на изготовление продукции. Тогда спецификация имеющегося сырья может быть представлена в виде вектора-столбца
‑го вида, идущего на изготовление продукции. Тогда спецификация имеющегося сырья может быть представлена в виде вектора-столбца
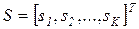 .
.
По аналогии с формулой (3.11), спецификация сырья, подлежащего обработке при плане производства 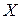 , определится выражением
, определится выражением
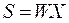 . (3.15)
. (3.15)
Каждый из видов сырья характеризуется стоимостью (или объемом) единицы измерения 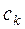 , (
, ( 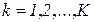 ), и
), и  эти показатели тоже можно объединить в виде вектора
эти показатели тоже можно объединить в виде вектора 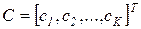 .
.
Общая стоимость сырья, использованного в соответствии с планом производства 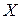 с учетом (3.15) равна
с учетом (3.15) равна
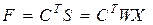 . (3.16)
. (3.16)
В формуле (3.16) вектор-строка 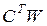 определяет стоимость сырья, обрабатываемого по
определяет стоимость сырья, обрабатываемого по 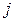 -й технологической карте.
-й технологической карте.
Часто при планировании производства учитывают отходы сырья. Пусть 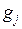 , (
, ( 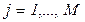 ) -количество отходов, образующихся при обработке сырья по
) -количество отходов, образующихся при обработке сырья по 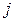 ‑й технологической карте. Тогда суммарные отходы, получаемые при плане производства
‑й технологической карте. Тогда суммарные отходы, получаемые при плане производства 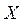 , определятся выражением
, определятся выражением
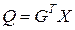 , (3.17)
, (3.17)
где 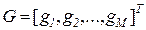 .
.
3.3 Задачи оптимального планирования производства
Приведенные в п. 3.2 соотношения позволяют формулировать задачи оптимального планирования производства [10]. Для этого предварительно необходимо проделать следующие операции:
· составить все необходимые технологические карты, на их основе рассчитать матрицы 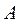 и
и 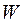 , а также определить векторы
, а также определить векторы 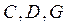 .
.
· принять решение о критерии оптимизации. В частности, таким критерием может быть:
а) максимум выхода продукции 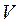 (3.14),
(3.14),
б) минимум расхода сырья 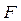 (3.16),
(3.16),
в) минимум отходов 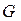 (3.17).
(3.17).
В практике планирования производства возможны различные постановки задач оптимизации. Ниже рассмотрены три наиболее типичных случая.
Первый случай планирования
Заданы:
· спецификация вырабатываемой продукции  ,
,
· матрицы 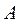 и
и 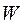 ,
,
· векторы 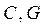 ,
,
Требуется определить:
· оптимальную по выбранному критерию спецификацию сырья – вектор 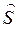 ;
;
· план производства 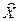 , обеспечивающий получение спецификации
, обеспечивающий получение спецификации 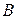 .
.
Последнее условие запишется в виде равенства
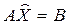 . (3.18)
. (3.18)
Поскольку спецификация сырья заранее не ограничена и можно выбирать любое сырье, то справедливо неравенство
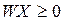 . (3.19)
. (3.19)
Критерии оптимизации могут быть двух видов:
· минимум расхода сырья
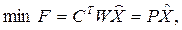 где
где 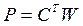 ; (3.20)
; (3.20)
· или минимум отходов
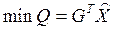 . (3.21)
. (3.21)
Использование в качестве критерия максимума выхода продукции (2.17) в рассматриваемой задаче не имеет смысла, т.к. спецификация продукции жестко задана.
Задачи (3.18), (3.19), (3.20) и (3.18), (3.19), (3.21) представляют собой задачи линейного программирования, которые можно решить с помощью стандартных программ, реализующих алгоритм симплекс-метода. Решив эти задачи и получив оптимальный вектор 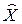 , можно затем определить искомую оптимальную спецификацию сырья (вектор
, можно затем определить искомую оптимальную спецификацию сырья (вектор 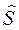 ):
):
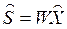 . (3.22)
. (3.22)
Второй случай планирования
Заданы:
· спецификация сырья 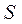 ,
,
· матрицы 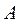 и
и 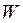 ,
,
· векторы 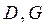 .
.
Требуется определить:
· оптимальную по выбранному критерию спецификацию вырабатываемой продукции 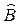 ,
,
· план производства 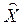 , обеспечивающий полное использование сырья и получение оптимальной спецификации продукции
, обеспечивающий полное использование сырья и получение оптимальной спецификации продукции 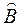 .
.
В этом случае задача оптимизации ставится следующим образом: найти такой оптимальный план производства 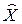 , который удовлетворяет ограничениям
, который удовлетворяет ограничениям
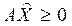 , (3.23)
, (3.23)
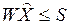 (3.24)
(3.24)
и обеспечивает экстремум одного из критериев:
· максимум выпуска продукции 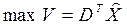 , (3.25)
, (3.25)
· минимум отходов 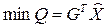 . (3.26)
. (3.26)
Использование в качестве критерия оптимизации минимума расхода сырья в данной постановке невозможно, т.к. объемы сырья заданы. Как и в предыдущем случае, решив с помощью стандартной программы задачи (3.23), (3.24), (3.25) или (3.23), (3.24), (3.26), получим оптимальный план производства 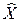 , а затем искомую оптимальную спецификацию продукции
, а затем искомую оптимальную спецификацию продукции
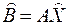 . (3.27)
. (3.27)
Третий случай планирования
Это наиболее распространенный случай планирования производства, он заключается в следующем.
Заданы:
· спецификация сырья 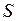 ,
,
· плановая спецификация вырабатываемой продукции 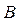 ,
,
· матрицы 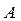 и
и 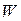 ,
,
· векторы 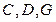 .
.
Требуется определить оптимальный по выбранному критерию план производства продукции 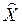 из имеющегося в наличии сырья
из имеющегося в наличии сырья 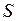 с целью выполнения заданной спецификации продукции
с целью выполнения заданной спецификации продукции 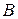 .
.
В данном случае ограничения имеют вид
· 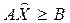 , (3.28)
, (3.28)
· 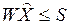 , (3.29)
, (3.29)
а критерий оптимальности задается одним из выражений:
· максимум выпуска продукции
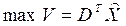 , (3.30)
, (3.30)
· минимум отходов
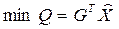 , (3.31)
, (3.31)
· минимум расхода сырья
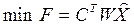 . (3.32)
. (3.32)
Найдя план производства 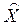 как решение неравенств (3.28), (3.29) с условиями (3.30), (3.31) или (3.32), необходимо затем вычислить фактические спецификации вырабатываемой продукции
как решение неравенств (3.28), (3.29) с условиями (3.30), (3.31) или (3.32), необходимо затем вычислить фактические спецификации вырабатываемой продукции 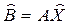 и используемого сырья
и используемого сырья 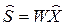 .
.
Пример. Рассмотрим пример принятия решения о производстве пиломатериалов из круглых бревен [10].
Требуется составить план раскроя бревен четырех размерных групп со средними диаметрами вершинной части 38. 42, 46 и 50 сантиметров на пиломатериалы 12 сечений с использованием 12 технологических карт (поставов). При этом нужно выполнить заданную спецификацию пиломатериалов и обеспечить минимум расхода сырья.
Характеристики сырья приведены в таблице 3.2, а характеристики карт раскроя – в таблице 3.1.
Таблица 3.2
Характеристики сырья
| Средний диаметр, см | ||||
| Объем1 бревна, куб. м. | 0,73 | 0,89 | 1,08 | 1,26 |
| Запас сырья данного вида,штук |



.
Плановая спецификация вырабатываемых пиломатериалов определена таблицей 3.3.
Таблица 3.3
План выработки пиломатериалов
| Номер сечения | |||||||||||
| План выработки пиломатериалов, куб.м. |
Поскольку и спецификация сырья, и спецификация пиломатериалов заданы, мы имеем третий случай планирования производства, причем критерием оптимальности служит минимум расхода сырья.
Выпишем все исходные данные задачи. Матрица  определится таблицей 3.1.
определится таблицей 3.1.
Матрица применимости карт раскроя к видам сырья также определяется таблицей 3.1 и имеет вид
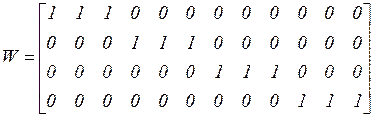 . (3.33)
. (3.33)
Векторы спецификаций сырья и пиломатериалов определяются соответственно таблицами 3.2 и 3.3 и имеют следующий вид.
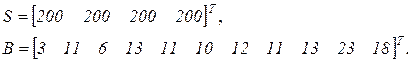 (3.34)
(3.34)
Вектор расхода сырья по каждой карте раскроя  определится объемами бревен тех размерных групп, к которым применима данная карта раскроя. На основе таблицы 3.1 вычислим вектор
определится объемами бревен тех размерных групп, к которым применима данная карта раскроя. На основе таблицы 3.1 вычислим вектор

Задача формулируется следующим образом: определить, сколько штук бревен 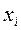 нужно раскроить с помощью каждой из имеющихся карт
нужно раскроить с помощью каждой из имеющихся карт 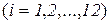 , т.е. найти такой план раскроя
, т.е. найти такой план раскроя
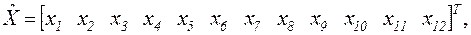 (3.35)
(3.35)
который бы удовлетворял системе ограничений
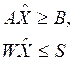 (3.36)
(3.36)
и доставлял минимум критерию
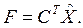 (3.37)
(3.37)
Сформулированная задача решалась с использованием стандартной программы, реализующей симплекс-метод. В результате расчета были выбраны карты раскроя с номерами 3, 6, 7, 9 и 10, а остальные карты не использовались. Полученный вектор оптимального выпуска продукции после округления значений 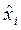 до ближайшего целого числа имеет вид
до ближайшего целого числа имеет вид
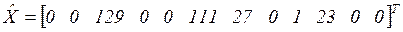 (3.38)
(3.38)
При этом фактически будет выработана следующая спецификация продукции (в куб.м):
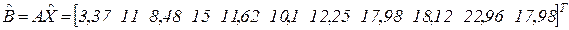
Мы видим, что план по выпуску продукции выполнен, а по ряду позиций – и перевыполнен.
Фактически израсходовано следующее количество сырья (штук бревен):
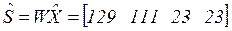 . (3.39)
. (3.39)
Сравнивая полученные цифры с заданной спецификацией (3.34), мы видим, что получилась значительная экономия сырья.
Значение критерия оптимизации (общий объем израсходованного сырья) составил
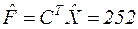 (куб.м). (3.40)
(куб.м). (3.40)
3.4 Транспортная задача
В качестве следующего примера задачи оптимизации при принятии решений рассмотрим так называемую транспортную задачу, которая также часто встречается на практике [26].
Задача формулируется следующим образом. Имеются склады, запасы на которых известны. Известны потребители и объемы их потребностей. Необходимо доставить товар со складов потребителям. Можно по-разному организовать «прикрепление» потребителей к складам, т.е. установить, с какого склада какому потребителю и сколько вести. Кроме того, известна стоимость доставки единицы товара с определенного склада определен-ному потребителю. Требуется минимизировать издержки по перевозке.
Пусть имеется 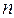 складов, на каждом из которых имеется запас продукции
складов, на каждом из которых имеется запас продукции











