Типовые задачи и методические указания по их решению

Задача 1. Определить натуральную длину отрезка АВ (А₁В₁; А₂В₂) и углы его наклона к плоскостям проекций (рис.1, рис.2).

Рис. 1 Рис. 2

Решение. Строим прямоугольный треугольник по двум катетам (см. рис.1). За один катет принимаем фронтальную проекцию А₂В₂ отрезка АВ, за другой катет – отрезок, равный разности расстояний концов отрезка до плоскости П₂. В₀В₂ = А₁А₁^/. Угол β - угол наклона АВ к плоскости проекций П₂.

Можно найти длину отрезка АВ, строя прямоугольный треугольник не на фронтальной проекции А₂В₂, а на горизонтальной проекции А₁В₁ (рис.2). Тогда вторым катетом будет разность расстояний концов отрезка до плоскости П₁. В₁В₀ = В₂В₂^/. Угол α - угол наклона отрезка АВ к плоскости проекций П₁.

Задача 2. На прямой l (l₁, l₂) от точки А(А₁, А₂) отложить отрезок длиной 30 мм (рис.3).

Решение. Выделяем на прямой l произвольный отрезок АМ и определяем его натуральную длину. Для этого строим прямоугольный треугольник по двум катетам А₁М₁ и М₁М₀ = М₂М₂^/ .

На гипотенузе А₁М₀ построенного треугольника откладываем отрезок А₁С₀ = 30 мм. Опустив из точки С₀ перпендикуляр на горизонтальную проекцию прямой, получаем горизонтальную проекцию А₁С₁ , а по ней и фронтальную А₂С₂ проекции искомого отрезка.

Рис. 3

Задача 3. Через прямую l (l₁, l₂) (рис.11а) провести фронтально проецирующую плоскость ∆ (рис.4).

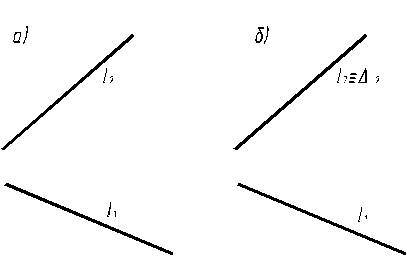
Рис. 4

Решение. Признаком принадлежности прямой l фронтально проецирующей плоскости является принадлежность (совпадение) фронтальной проекции l₂ , прямой l с фронтальной проекцией ∆₂ плоскости ∆ ,

т.е. если l Ì ∆ Û l₂ ≡ ∆₂ (рис.4 б).

Задача 4. Построить проекции линии пересечения двух плоскостей Г(АВС) и ∆ ( ∆ ₂ ) (рис.5а).

Рис. 5

Решение. Плоскость ∆ ( ∆ ₂) – фронтально проецирующая. Фронтальная проекция плоскости ∆ обладает собирательным свойством, поэтому фронтальная проекция N₂M₂ искомой линии пересечения совпадает с ∆ ₂. Пользуясь условием, что искомая прямая MN принадлежит и плоскости Г (АВС), находим по фронтальной проекции её горизонтальную проекцию M₁N₁ (рис.5 б).

Задача 5. Построить проекции точки пересечения прямой l (l₁, l₂) с плоскостью Г(АВС). Определить видимость прямой l (l₁, l₂) относительно плоскости Г (рис.6 а).

Решение. Для решения задачи следует последовательно выполнить следующие три операции (рис.6 б).

1-я операция. Через прямую l провести фронтально проецирующую плоскость ∆ (∆ ₂ ) (см. задачу 3).

2-я операция. Построить проекции линии пересечения обеих плоскостей – данной Г и вспомогательной ∆, т.е. MN (M₁N₁; M₂N₂) (см. задачу 4).

3-я операция. В пересечении проекций данной прямой l и построенной MN отметить проекции (К₁, К₂) искомой точки.

Рис. 6

Найдя точку пересечения, перейти к определению видимости прямой l .

Для определения видимости прямой l на горизонтальной проекции (вид сверху) рассматриваем две горизонтально конкурирующие точки 1 Î АВ и 2 Î l (1₁ ≡ 2₁). По фронтальной проекции видим, что точка 1 лежит по отношению к плоскости П₁ выше, чем точка 2. Это значит, что сверху видимой является точка 1, а точка 2 закрыта ею. Следовательно, на виде сверху отрезок прямой l , на котором лежит точка 2, является невидимым. На фронтальной проекции видимость можно определить, например, при помощи фронтально конкурирующих точек N Î ВС и 3 Î l . Сравниваем расстояние их по отношению к плоскости П₂ . Сравнение показывает, что точка 3 прямой l , а следовательно, отрезок 3К, спереди не виден.

Задача 6. В плоскости Г (l ∩ m) провести горизонталь h (h₁, h₂) и фронталь f ( f₁; f₂) (рис.7а).

Рис. 7

Решение. Известно, что фронтальная проекция h₂ горизонтали h всегда параллельна оси XO. Поэтому построение горизонтали начинаем с проведения h₂ ∥ XO (рис.7б). Горизонтальную проекцию находим из условия принадлежности горизонтали h плоскости Г. Фронтальная проекция горизонтали пересекает фронтальные проекции данных прямых l₂ и m₂ в точках 1₂ и 2₂ , которым соответствуют горизонтальные проекции 1₁ и 2₁. Через них и пройдет горизонтальная проекция h₁ искомой горизонтали h . На (рис.7б) в плоскости Г построена и фронталь f (f₁; f₂). Это построение выполнено аналогично построению горизонтали.

Задача 7. Даны плоскость Г (l ‌ || ‌ m) и точка D(D₁; D₂).

Опустить перпендикуляр из точки на эту плоскость (рис.8).

Известно, что если прямая перпендикулярна плоскости, необходимо, чтобы горизонтальная проекция прямой была перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция – фронтальной проекции фронтали плоскости.

Решение . Проводим горизонталь h (h₁; h₂ ) и фронталь f ( f₁; f₂) (см. задачу 6). Затем проводим проекции перпендикуляра: горизонтальную n₁ – через D₁ перпендикулярно горизонтальной проекции горизонтали h₁ , и фронтальную n₂ – через D₂ перпендикулярно проекции фронтали f₂ .

Рис. 8

Задача 8. Из произвольной точки плоскости Г (l ∩ m) восстановить перпендикуляр (нормаль) к плоскости (рис.9а).

Решение. Признаки перпендикулярности прямой и плоскости позволяют строить на чертеже проекции нормали к плоскости. На рис.16б дано построение нормали n ( n₁; n₂) в точке К (К₁ ; К₂) к плоскости Г (l ∩ m). Проекции нормали перпендикулярны соответствующим проекциям линий уровня плоскости Г.

Рис. 9

Задача9. Даны плоскость Г (l ∩ m) и точка D; требуется определить расстояние от точки D до плоскости, заданной двумя пересекающимися прямыми l и m (рис. 10).

Рис. 10

Порядок решения задачи:

1. Опустить перпендикуляр из точки D на плоскость Г (l ∩ m) (см. задачу 7).

2. Определить точку пересечения перпендикуляра с плоскостью и отделить видимый участок перпендикуляра от невидимого, считая плоскость непрозрачной (см. задачу 5).

3. Определить натуральную величину расстояния от точки D до плоскости Г (см. задачу 1).

Задача 10. Дана точка К(К₁;К₂) и плоскость Г (АВС) провести через точку К плоскость, параллельную заданной плоскости Г (рис. 11).

Построение эпюра параллельных плоскостей основано на известном из стереометрии признаке: если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Рис. 11

Решение. Проводим через точку К(К₁;К₂) прямые l (l₁, l₂) и m (m₁ ; m₂), параллельно сторонам АВ(А₁ В₁,А₂ В₂) и АС(АС₁,АС₂). Плоскости Г и Ʃ параллельны, т.к. их пересекающиеся прямые удовлетворяют условию: l ∥ АВ и m ∥ АС.

Задача 11. Построить плоскость ∆, параллельную плоскости Г (АВС) и отстоящую от неё на расстоянии 40 мм (рис. 12).

План решения задачи:

1. Из произвольной точки С (С₁;С₂) заданной плоскости восстановить перпендикуляр к ней и ограничить его точкой N(N₁;N₂) (см. задачу 8).

2. Определить натуральную величину отрезка перпендикуляра по его проекции C₁N₁ и C₂N₂ (см. задачу 1).

Рис. 12

3. На действительной величине отрезка перпендикуляра найти точку М₀ на заданном расстоянии, считая от плоскости, и построить проекции этой точки М(М₁;М₂) на проекциях перпендикуляра (см. задачу 2).

4. Задать искомую плоскость, соблюдая условие параллельности плоскостей (см. задачу 10).

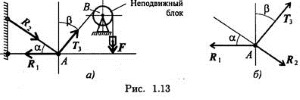
Задача 12. Через прямую l (l₁,l₂) провести плоскость ∆, перпендикулярную к плоскости Г (m ∩ n) (рис.13).

Решение. Если плоскость содержит в себе перпендикуляр к другой плоскости, то эти плоскости взаимно перпендикулярны. Чтобы провести через прямую l (l₁, l₂) искомую плоскость, надо из какой-либо точки прямой, например, А(А₁;А₂), провести перпендикуляр к данной плоскости.

Строим проекции горизонтали h(h₁;h₂) и фронтали f(f₁;f₂) плоскости Г(n ∩ m). Затем, проведя А₁В₁ ^ h₁ и А₂В₂ ^ f₂ , получим проекции перпендикуляра к плоскости Г. Этот перпендикуляр АВ (А₁В₁; А₂В₂) совместно с данной прямой l (l₁, l₂) определяют искомую плоскость Δ (l ∩ АВ).

Рис. 13

Задача 13. Построить линию пересечения двух плоскостей Г(АВС) и ∆(DEF) и отделить видимые их части от невидимых (рис.14).

Рис. 14

Решение. Первая часть задачи сводится к построению линии пересечения двух плоскостей.

Известно, что линией пересечения двух плоскостей является прямая линия, для построения которой достаточно определить две точки, общие обеим плоскостям. В данном случае общие точки для обеих плоскостей найдены как точки пересечения: М – стороны DE треугольника DEF с плоскостью Г(АВС); N – стороны ВС треугольника АВС с плоскостью ∆(DEF). Точка М определена с помощью вспомогательной фронтально проецирующей плоскости θ(θ₂), точка N – посредством горизонтально проецирующей плоскости Σ(Σ₁) проведенных через DE и BC соответственно.

Линия пересечения плоскостей ограничена отрезком MN прямой, заключённым между точками встречи контура одной фигуры с ограниченной плоскостью другой.

Найдя линию пересечения, переходим к отделению видимых участков пластинок от невидимых, начав с горизонтальной проекции (вид а сверху). С этой целью рассмотрим две горизонтально конкурирующие точки 5 Î АВ и 6 Î DE. Сравнивая расстояния фронтальных проекций этих точек по отношению к плоскости П₁. замечаем, что точка 6 пластинки DEF, а следовательно, и участок стороны DE, находится под плоскостью пластинки АВС. В точке М происходит переход невидимого участка прямой DE к видимому.

Аналогичными рассуждениями при помощи фронтально конкурирующих точек 1 Î АВ и 7 Î DE определяем видимость на фронтальной проекции.

Задача 14. Дана точка А(А₁;А₂). Найти её проекции в системе П₁/П₄ (рис.15а).

На рис. 15 показаны те построения, которые надо произвести на эпюре, чтобы от проекций точки А(А₁;А₂) в системе П₁/П₂ перейти к проекциям (А₁;А₄) той же точки в системе П₁/П_4..

1.Опускаем из А₁ перпендикуляр на новую ось проекций П₁/П₄. На построенном перпендикуляре откладываем (от новой оси) отрезок А₄А_х'=А₂А_х.

Полученная таким образом точка А₄ является проекцией точки А(А₁;А₂) на новую плоскость проекции П₄.

Задача 15. Дана точка А(А₁;А₂) найти её проекции в системе П₂/П₄ (рис.15б).

На рис.15б показаны те построения, которые надо произвести на эпюре, чтобы от проекции (А₁;А₂) точки А в системе П₁/П₂ перейти к проекциям (А₂; А₄) той же точки в системе П₂/П ₄ .

Рис. 15

Для построения на эпюре новой проекции точки при замене одной из плоскостей проекций надо опустить перпендикуляр на новую ось из той же проекции точки, которая не меняется, и отложить на нем от новой оси в соответствующую сторону расстояние от заменяемой проекции до старой оси.

Задача 16. Преобразовать горизонтально проецирующую плоскость Г(АВСD) в плоскость уровня (рис.16).

Решение. Плоскость Г – горизонтально проецирующая. Для преобразования ее в плоскость уровня достаточно взамен плоскости проекции П₂ ввести новую плоскость П₄ , параллельную плоскости Г(АВСD). Линию пересечения плоскостей П₁ и П₄ принимаем за новую ось проекций X₁.

Новая ось X₁ параллельна вырожденной проекции Г₁ плоскости Г, т.к. плоскость П₄ параллельна данной плоскости Г.  Построив проекции точек А, В, С и D в новой системе П₁ П₄ и соединив их, получим проекцию четырехугольника А₄В₄С₄D₄, отображающего свои натуральные размеры.

Рис. 16

Задача 17. По данной фронтальной проекции К₂ точки К построить горизонтальную проекцию К₁, исходя из условия, что точка К принадлежит грани SАС (рис.17).

Построение точки на поверхности выполняется как построение точки на плоскости грани.

Решение. На грани SАС при помощи прямой 1–2 (1₁2₁ ; 1₂2₂) по данной фронтальной проекции К₂ точки К построена горизонтальная проекция К₁ , исходя из условия, что точка К должна лежать в грани SАС.

На рис.18 показано построение К₁ на грани SВС при помощи прямой, проведенной через вершину S пирамиды.

Рис. 17 Рис. 18

Задача 18. Задать на поверхности конуса произвольную точку А (рис.19).

Рис. 19

Решение.

1-й способ (рис.19а). На основании конуса задаем произвольную точку К(К₁ , К₂) и проводим вспомогательную образующую через точки S и К. На этой образующей берем точку А, которая и лежит на заданной поверхности.

2-й способ (рис.19б). На поверхности конуса проводим вспомогательную параллель; ее фронтальная проекция является отрезком прямой, параллельным оси проекций XO, а горизонтальная проекция – окружностью. На этой параллели берем точку А , которая и лежит на поверхности.

Задача 19. Построить горизонтальную проекцию линии на поверхности конуса по заданной фронтальной проекции (рис.20).

Решение. Построение горизонтальной проекции заданной линии начинаем с того, что отмечаем точки, принадлежащие очерковым образующим. Эти точки называют характерными.

Точка 3 принадлежит передней образующей, 8 – задней, 2 – правой, 1 – левой и точка 10 – основанию конуса. Между этими точками отмечают так называемые случайные точки, помогающие установить характер линии. Точки 4, 5, 6, 7 и 9 – случайные.

Горизонтальные проекции всех отмеченных точек находим из условия принадлежности их конусу (см. задачу 16).

Рис. 20

При соединении точек следует учитывать их видимость. В нашем примере все точки сверху видимы, поэтому и линия, соединяющая их, видима сверху.