Примеры решения задач. Определение грузоподьемности центрально-сжатого стержня
Определение грузоподьемности центрально-сжатого стержня
Условие задачи. Стержень, показанный на рис. 6.3, а, загружен сжимающей силой F. Поперечное сечение стержня, состоящее из двух швеллеров № 30 и двух планок, соединенных со швеллерами четырьмя болтами, изображено на рис. 6.3, б. Размер планок 400´12 мм, диаметр болтов 20 мм. Материал – сталь С235 с 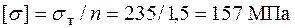 .
.
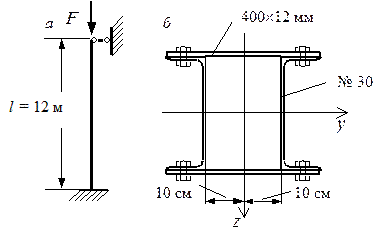
Рис. 6.3. Условие задачи № 34: а – сжатый стержень; б – поперечное сечение стержня
Требуется:
1) найти значение критической нагрузки;
2) определить допускаемую нагрузку так, чтобы выполнялись условия устойчивости и прочности стержня;
3) вычислить нормируемый коэффициент запаса устойчивости.
Решение. Прежде всего найдем моменты инерции поперечного сечения относительно главных центральных осей. Сечение имеет две оси симметрии (оси y и z на рис. 6.3, б), поэтому эти оси и будут главными центральными осями инерции сечения. Моменты инерции относительно этих осей определяем, используя данные из сортамента прокатной стали и формулы (5.16), (5.17):
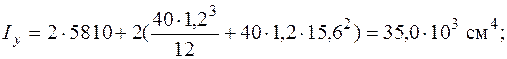
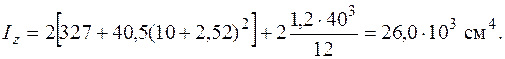
Минимальным оказался момент инерции относительно оси z. Определяем площадь сечения
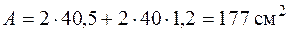
и минимальный радиус инерции по формуле (5.10)
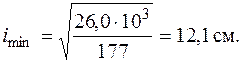
Теперь можно найти гибкость стержня. Для заданного условия закрепления стержня в соответствии с рис. 6.2,б коэффициент 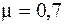 . Тогда по формуле (6.1)
. Тогда по формуле (6.1)

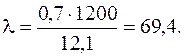
Сравним величину полученной гибкости стержня с характеристиками 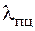 и
и 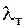 для стали С235. По формуле (6.5)
для стали С235. По формуле (6.5)
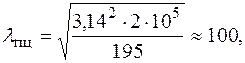
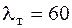 по таблице, приведенной в [4, с. 29],. Таким образом,
по таблице, приведенной в [4, с. 29],. Таким образом, 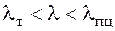 и для определения критической силы следует использовать формулу Ясинского (6.3):
и для определения критической силы следует использовать формулу Ясинского (6.3):
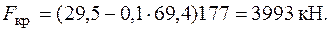
Значения коэффициентов a и b в формуле Ясинского взяты из таблицы на с. 29 [4] и переведены из МПа в кН/см2.
Найдем допускаемую нагрузку из условия устойчивости по формуле (6.7). Для определения коэффициента  используем таблицу на с. 370 [2][16]. Интерполируем значения
используем таблицу на с. 370 [2][16]. Интерполируем значения  , заданные в таблице:
, заданные в таблице: 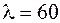 соответствует
соответствует 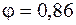 , а
, а 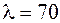 –
– 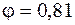 . Тогда гибкости
. Тогда гибкости 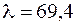 рассматриваемого стержня соответствует
рассматриваемого стержня соответствует 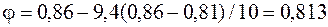 . Значение допускаемой нагрузки
. Значение допускаемой нагрузки
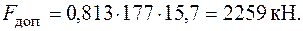
Проверим, удовлетворяет ли найденная допускаемая нагрузка условию прочности (6.8). Вычислим площадь нетто, уменьшив полную площадь сечения на площадь, занимаемую четырьмя отверстиями под болты[17]:
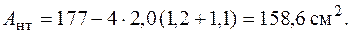
Тогда условие прочности
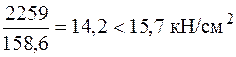
выполняется.
В заключение найдем нормируемый коэффициент запаса устойчивости по формуле (6.9):
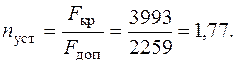
Коэффициент запаса устойчивости находится в пределах 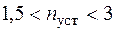 .
.
Дата добавления: 2016-11-29; просмотров: 1510;











