Примеры решения задач и последовательность решения задач

Последовательность решения задач:
1. Выбрать тело (точку), равновесие которого следует рассматри­вать.
2. Освободить тело (шарнир) от связей и изобразить действую­щие на него активные силы и реакции отброшенных связей. Причем реакции стержней следует направить от шарнира, так как принято предполагать, что стержни растянуты.

3. Выбрать оси координат и составить уравнения равновесия, ис­пользуя условия равновесия системы сходящихся сил на плоскости ∑Xi = 0; ∑Yi = 0. Выбирая оси координат, следует учитывать, что полученные уравнения будут решаться проще, если одну из осей напра­вить перпендикулярно одной из неизвестных сил.
4 .Определить реакции стержней из решения указанной системы уравнений.
5. Проверить правильность полученных результатов, решив уравне­ния равновесия относительно заново выбранных координат х и у.

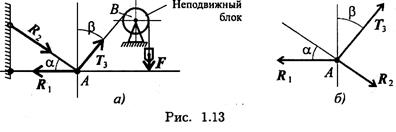
Пример 1. Груз подвешен на стержнях и канатах и находится в равновесии (рис. 1.13). Изобразить систему сил, действующих на шарнир А.

Решение

1.  Реакции стержней направлены вдоль стержней, реакции гибких связей направлены вдоль нитей в сторону натяжения (рис. 1.13, а).

2. Для определения точного направления усилий в стержнях мысленно убираем последовательно стержни 1 и 2. Анализируем воз­можные перемещения точки А.

Неподвижный блок с действующими на него силами не рассмат­риваем.

3. Убираем стержень 1, точка А поднимается и отходит от стены, следовательно, реакция стержня 1 направлена к стене.

4. Убираем стержень 2, точка А поднимается и приближается к стене, следовательно, реакция стержня 2 направлена от стены вниз.

5. Канат тянет вправо.

6. Освобождаемся от связей (рис. 1.13, б).

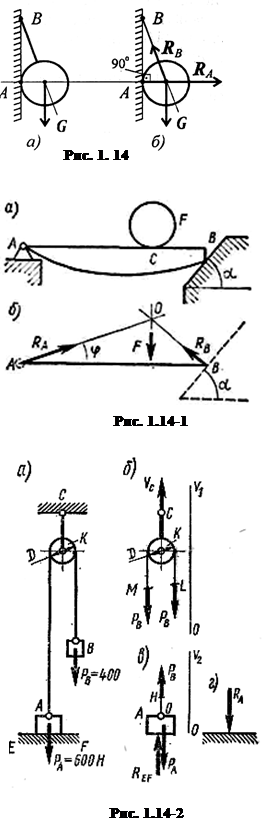
Пример 2. Шар подвешен на нити и опирается на стену (рис. 1.14а). Определить реакции нити и гладкой опоры (стенки).

Решение

1. Реакция нити — вдоль нити к точке В вверх (рис. 1.14, б).

2. Реакция гладкой опоры (стен­ки) — по нормали от поверхности опоры.

Пример 3. Представим, что на горизонтально расположенный брус АБ, собственной массой которого пренебрегаем, действует вертикальная нагрузка F, приложенная в точке С бруса (рис. 1.14-1, а). Левый конец бруса А прикреплен к опоре шарниром, а правый В опира­ется на гладкую наклонную плоскость.

Изобразим брус схематично отрезком АВ, как на рис. 1.14-1, б, и приложим к нему в точке С вертикальную силу F. В точке В со стороны наклонной плоскости к брусу приложена ее реакция R_B, направленная перпендикулярно плоскости; линии действия сил F и R_B пересекаются в точке О. Кроме этих сил на брус действует еще одна сила — реакция шарнирно-неподвижной опоры. А так как брус находится в равновесии, то линия действия третьей силы также пройдет через точку О, т. е. реакция R шарнир-но-неподвижной опоры направлена вдоль отрезка АО.

Примененный здесь метод рассуждения называется принципом освобождения тела от связей и замены связей их реакциями.

Пример 4. Определить усилие в стержне CD и силу давления груза А на опорную плоскость EF (рис. 1.14-2, а). Массой стержня CD, блока К, каната и трением каната о блок пренебречь.

Решение. Натяжение кана­та во всех его точках одина­ково и равно силе тяжести груза В, так как неподвиж­ный блок изменяет только направление силы, действую­щей на канат.

Рассмотрим равновесие си­стемы: стержень CD и блок К с прилегающим к нему отрезком каната ML. Отбросим связи и заменим их действие соответствующими реакциями (рис. 1.14-2, 6). Для полученной системы сил можно соста­вить только одно уравнение равновесия:

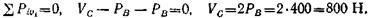
На рис. 1.14-2, в показаны силы, действующие на груз А с прилегающим к нему отрезком каната ОН. R_EF — реак­ция опорной плоскости.

Так как груз А находится в равновесии, то

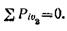
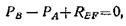
откуда

R_еf = Pa – Рв = 600 – 400 = 200 Н.

Сила давления груза А на опорную плоскость RA показана на рис, 1.14-2, г. Очевидно, R_A = R_EF = 200 H (сила действия равна силе противодействия).

Пример 5. Определить реакции стержней, удерживающих грузы F₁ = 70 кН и F₂ = 100 кН (рис. а). Массой стержней пренебречь.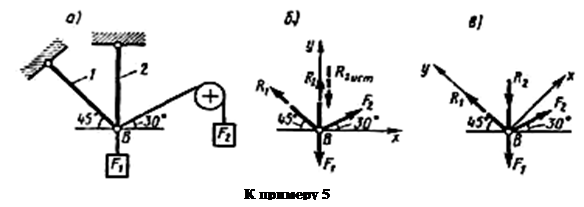 

Решение

1. Рассматриваем равновесие шарнира В (рис. а).

2. Освобождаем шарнир В от связей и изображаем действующие на него активные силы и реакции связей (рис. б).

3. Выбираем систему координат, совместив ось у по направлению С реакцией R₂ (рис. б) и составляем уравнения равновесия для системы сил, действующих на шарнир В:

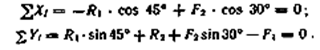
3. Определяем реакции стержней R₁ и R₂, решая уравнения.

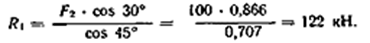
Подставляя найденное значение R₁ в уравнение (2), получаем

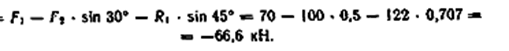
Знак минус перед значением R₂ указывает на то, что первоначально выбранное направление реакции неверное — следует направить реак­цию R₂ в противоположную сторону, т.е. к шарниру В (на рис. б истинное направление реакции R₂ показано штриховым вектором).

5. Проверяем правильность полученных результатов, выбрав новое расположение осей координат х и у (рис. а). Относительно этих осей составляем уравнения равновесия:

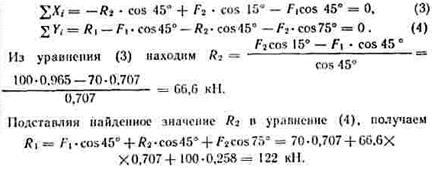
Значения реакций R₁ и R₂, полученные при решении уравнений (1) и (2), совпадают по величине и направлению со значениями, найденными из уравнений (3) и (4), следовательно, задача решена правильно.

Контрольные вопросы и задания

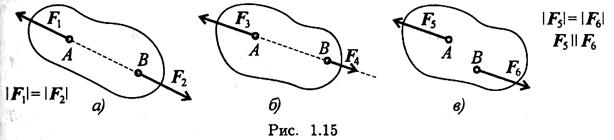
1. Какая из приведенных систем сил (рис. 1.15) уравновешена? 

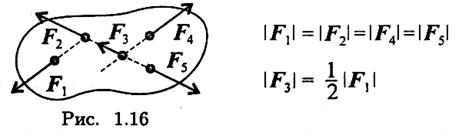
2. Какие силы системы (рис. 1.16) можно убрать, не нарушая механического состояния тела:

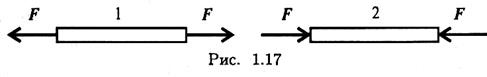
3. Тела 1 и 2 (рис. 1.17) находятся в равновесии. Можно ли убрать действующие системы сил, если тела абсолютно твердые? Что изменится, если тела реальные, деформируемые?

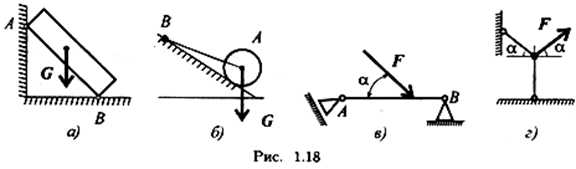
4. Укажите возможное направление реакций в опорах (рис. 1.18).