В ЭЛЕКТРОННО-ВОЗБУЖДЕННЫХ СОСТОЯНИЯХ
Сведения об электронном строении и свойствах органических соединений в возбужденных состояниях очень скудны. Они сравнительно мало доступны для эксперимента, и возможность привлечения методов квантовой химии представляется очень важной. Следует отметить, что изучение возбужденных состояний имеет большое значение не только для характеристики оптических свойств молекул, но и для понимания особенностей и механизмов фотохимических реакций.
Приближение Хартри - Фока для молекул с замкнутой оболочкой, описанное в гл. 1, позволяет рассчитать волновую функцию основного состояния Ψо. При изучении электронно-возбужденных состояний в схему расчета необходимо внести некоторые изменения. Наиболее простой модификацией является приближение виртуальных орбиталей [170], в котором все одноэлектронные МО рассчитываются стандартным методом Хартри - Фока для основного состояния при расположении на каждой занятой МО пары электронов с противоположными спинами. После нахождения самосогласованных коэффициентов разложения МО по АО, энергий МО и полной энергии молекулы, один из электронов "переносится" с занятой МО m на вакантную МО r. Энергию такого перехода вычисляют как разность энергий электрона на этих МО:
Е(m→r) = Е(r) -Е(m) - (Jmr – 2Kmr),
где Jmr и Kmr - кулоновский и обменный интегралы,
Jmr= <mm|rr>; Kmr= <mr|mr>.
Величина (Jmr – 2Kmr) учитывает образование вакансии на МО m при электронном переходе m→z. Основной недостаток приближения виртуальных орбиталей заключается в том„ что все МО при электронном переходе считаются неизменными.
Другими способами, широко используемыми для изучения геометрии и электронной структуры молекул в возбужденных состояниях, являются ограниченный и неограниченный методы Хартри-Фока для открытых оболочек и полуэлектронный метод Дьюара.
Уравнения, необходимые для проведения расчетов ограниченным методом Хартри-Фока электронных волновых функций для соединений с открытыми оболочками, получены Рутаном [2]. Они значительно сложнее, чем для систем с замкнутыми оболочками, но в работах [171- 174] предложены вполне приемлемые способы их решения, и в настоящее время ограниченный метод Хартри-Фока применяется некоторыми авторами для неэмпирических расчетов геометрии возбужденных состояний. При использовании неограниченного метода Хартри-Фока для каждой электронной пары вводят два разных набора линейных комбинаций АО, соответствующих электронам с разными спинами. Каждое электронное состояние описывается своим набором коэффициентов, определяющих заселенность МО электронами. Коэффициенты разложения МО по АО определяются из системы уравнений, полученной в работе [175]. В этом приближении электроны перестают быть спаренными, энергии МО для электронов с разными спинами не совпадают (рис. 3.1). Основной недостаток неограниченного метода Хартри-Фока заключается в том, что найденная волновая функция не является собственной функцией квадрата спинового оператора. Таким образом, мы получаем неточное решение, которое может быть улучшено лишь введением дополнительной и весьма трудоемкой процедуры проектирования. Без проектирования энергии возбужденных состояний, вычисленные этим методом, получаются сильно заниженными.

Pис. 3.1. Заполнение МО электронами при расчете волновых функций возбужденных состояний
а — неограниченный метод Хартри—Фока; б — полуэлектронный метод Дьюара
В основу полуэлектронного метода Дьюара [176] положены стандартные уравнения Рутана для молекул с замкнутыми оболочками, когда на каждой МО находятся по два электрона, но с измененным числом электронов на двух МО, между которыми произошел электронный переход. Такое описание возбужденного состояния с сохранением стандартных формул ограниченного метода Хартри-Фока для систем с замкнутыми оболочками, по существу, означает заселение МО, занятых одним электроном, двумя половинками электрона с противоположными спинами (см. рис. 3.1). При этом в матричные элементы фокиана войдут интегралы кулоновского взаимодействия между половинками электрона, и неправильно будет учтено обменное взаимодействие между неспаренными электронами. Необходимые в связи с этим поправки Дьюар предложил ввести в итоговые величины полной энергии, сохранив стандартные выражения Рутана для вычисления матричных элементов фокиана. В таком приближении обычные программы для молекул с замкнутыми оболочками изменяются при переходе к изучению возбужденных состояний в наименьшей степени. При этом, однако, коэффициенты разложения МО по базису АО определяются с помощью минимизации неточного выражения для полной энергии. В этом заключается основной недостаток полуэлектронного метода Дьюара.
Наиболее точные результаты для электронно-возбужденных состояний можно получить методом конфигурационного взаимодействия (KB), краткое описание которого дано во введении. При использовании полуэмпирических методов обычно учитывают взаимодействие только между однократно возбужденными состояниями. В этом варианте метода KB волновые функции синглетных электронно-возбужденных состояний Ψm→r, вычисленные в приближении виртуальных орбиталей, составляют базисный набор:
Ψm→r= const det[φ1(1)α(1)φ1(1')β(1')...
...φm-1(m - 1)β(m - 1)φ(m')β(m')...
... φn(n)α(n)φn(n')β(n')φr(r)α(r)].
Линейные комбинации этих функций дают более точные волновые функции возбужденных состояний.
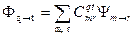
здесь m, r, q и t - индексы, которые могут варьироваться от 1 до N, где N - заданный размер матрицы KB (может варьироваться в широких пределах). Коэффициенты Сqtmr определяются диагонализацией матрицы, построенной из элементов <Ψm→r|H|Ψm’→r’>. Функции Ψm→r являются однодетерминантными, Фq→t, - многодетерминантными. Однако для большинства электронно-возбужденных состояний основной вклад в Фq→t дает только одна однодетерминантная функция, а другие вносят лишь небольшую поправку, отражающую изменение МО при возбуждении.
Таблица 3.2Геометрия молекул в нижнем синглетном электронно-возбужденном состоянии
| Метод | HCN | Н2СО | C2H2 | |||
| C—N, нм | Н-С-Н, град | С—О, нм | α*1, град | С—С, нм | Н-С-Н, град | |
| Вирт. МО, ППДП/2 KB ППДП/2 ОСТ-4ГФ 4-31 ГФ ОМХФ*2, МЧПДП/3 ПЭ*3, МЧПДГ/3 Эксперимент | 0,130 0,130 0,137 0,130 - - 0,130 | - - | 0,128 0,128 0,131 0,127 0,127 0,125 0,132 | 0,134 0,133 0,137 0,137 0,135 0,135 0,139 |
*1 Угол между плоскостью Н—С—Н и связью С=О.
*2 Ограниченный метод Хартри-Фока.
*3 Полуэлектронный метод Дьюара.
Преимущества и недостатки каждого из рассмотренных выше методов исследованы еще недостаточно, но, по-видимому, все они вполне пригодны для расчета геометрии и электронной структуры возбужденных состояний органических соединений. Примеры расчетов геометрии синглетных возбужденных состояний разными методами приведены в таблице 3.2. Согласие с экспериментом получается неплохое. При этом следует отметить, что для спектроскопии и фотохимии нужны не абсолютные значения геометрических параметров, приведенные в таблице, а их изменение при электронном возбуждении; последнее передается квантовохимическими методами намного точнее.
С точки зрения затрат машинного времени наиболее экономичным является полуэлектронный метод Дьюара [177], поэтому он наиболее широко используется в полуэмпирических расчетах. Неэмпирические вычисления чаще всего проводят неограниченным методом Хартри-Фока, однако это, по-видимому, связано с тем, что он включен в наиболее широко распространенные программы ГАУССИАН-76, -80 и -82.
Дата добавления: 2020-12-11; просмотров: 525;











