Теорема 1. (критерий подкольца).
Непустое множество 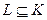 является подкольцом
является подкольцом 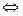
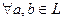 :
:
1) 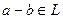 2)
2) 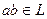 .
.
Доказательство.
Необходимость- очевидно. Если подкольцо, то произведение принадлежит, кроме того, 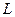 является подгруппой по сложению, тогда для любого
является подгруппой по сложению, тогда для любого 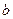 элемент
элемент 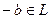 , а значит и
, а значит и 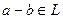 .
.
Достаточность.Если для любой пары элементов 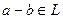 то и для пары одинаковых
то и для пары одинаковых 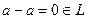 , а тогда и
, а тогда и 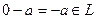 , то есть для каждого элемента противоположный тоже
, то есть для каждого элемента противоположный тоже 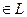 , т.е.
, т.е. 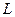 подгруппа по сложению (логика док-ва как в док. критерия подгруппы, только там общий вид операции
подгруппа по сложению (логика док-ва как в док. критерия подгруппы, только там общий вид операции 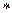 ).
).
Операция ассоциативна и на подмножестве, поэтому 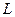 полугруппа.
полугруппа.
Дистрибутивность также сохраняется на подмножестве.
Вывод: 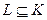 подкольцо.
подкольцо.
Обратимые элементы.
Определение. 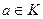 называется обратимым, если
называется обратимым, если 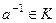 .
.
Пример. В кольце 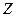 обратимые элементы только 1 и
обратимые элементы только 1 и 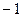 .
.
В кольцах 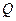 или
или 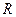 обратимые элементы все, кроме 0.
обратимые элементы все, кроме 0.
В кольце функций (с поточечным умножением) обратимые элементы это те функции, которые ни в одной точке не обращаются в 0.
Делители нуля
Определение.Если 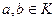 ,
, 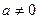 ,
, 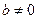 , но при этом
, но при этом 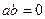 , то
, то 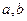 называются делителями нуля.
называются делителями нуля.
Пример в кольце функций. 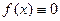 только на
только на 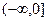
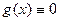 на
на 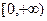 . Тогда
. Тогда 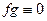 на всей числовой оси.
на всей числовой оси.
В числовых множествах делителей нуля нет. В кольце матриц есть, например, 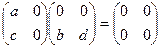 .
.
Теорема 2. Обратимый элемент кольца не может являться делителем нуля.
Доказательство. Пусть 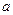 обратим, и пусть всё же он является делителем 0, тогда есть какой-то
обратим, и пусть всё же он является делителем 0, тогда есть какой-то 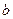 , что
, что 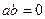 . Но тогда
. Но тогда
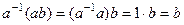 ,
,
но с другой стороны, 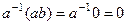 , тогда
, тогда 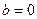 .
.
Значит, 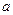 не делитель нуля.
не делитель нуля.
Замечание.Обратное утверждение к теореме 2 неверно, т.е. из того, что он не делитель нуля, не следует, что обратимый. Пример: в кольце 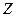 все не делители нуля, но из этого не следует, что они обратимы, там обратимы только 1 и
все не делители нуля, но из этого не следует, что они обратимы, там обратимы только 1 и 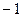 (выше был пример).
(выше был пример).
Теорема 3. О мультипликативной группе кольца.
Все обратимые элементы кольца 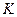 с единицей образуют группу по умножению. (Обозначается
с единицей образуют группу по умножению. (Обозначается 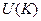 ).
).
Доказательство.
Докажем, что если 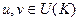 то
то 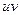 тоже обратим, т.е.
тоже обратим, т.е. 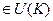 . Докажем, что обратный имеет такой вид:
. Докажем, что обратный имеет такой вид: 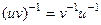 .
.
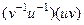 =
= 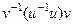 =
= 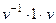 =
= 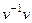 = 1.
= 1.
Кроме того, 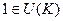 , ведь сам элемент 1 обратим, и обратный к нему тоже 1.
, ведь сам элемент 1 обратим, и обратный к нему тоже 1.
Обратный к любому элементу также 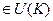 , ведь если он обратный к какому-то, и равен
, ведь если он обратный к какому-то, и равен 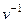 , то он автоматически обратим, обратный к нему это исходный
, то он автоматически обратим, обратный к нему это исходный 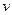 . □
. □
Идеал кольца.
Определение.Подкольцо 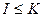 называется идеалом, если
называется идеалом, если 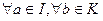
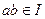 .
.
Пример во множестве функций. Все функции, обращающиеся в 0 в точке 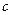 , образуют идеал. Если умножить произвольную функцию на такую, то произведение приобретает свойство
, образуют идеал. Если умножить произвольную функцию на такую, то произведение приобретает свойство 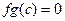 .
.
Кольца вычетов.
Определение.Два целых числа называются сравнимыми по модулю n, если при делении на n они дают одинаковые остатки, т.е. если их разность делится на n: 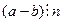 .
.
Обозначается 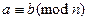 .
.
Например, числа 1, 4, 7, 10, 13, ... дают при делении на 3 остаток 1. При этом разность любых из них делится на 3.
Таким образом, множество 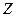 распадается на n непересекающихся классов.
распадается на n непересекающихся классов. 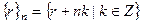 - класс вычетов по модулю n.
- класс вычетов по модулю n.
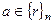 означает, что
означает, что 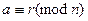 .
.
Дата добавления: 2020-12-11; просмотров: 1597;











