Теорема 4 (о размерности пространства решений).

Пусть дана линейная однородная система с 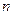неизвестными, ранг основной матрицы равен 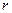. Тогда существует 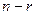линейно-независимых решений однородной системы, всякое другое решение есть их линейная комбинация.

Доказательство.

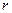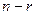1) Если ранг основной матрицы равен , то свободных переменных переносятся вправо, тогда можно построить по крайней мере не меньше, чем 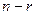линейно-независимых решений, присваивая поочерёдно значение 1 каждой из свободных переменных (а остальным в это время 0).

Существует такая система решений:

...

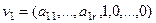
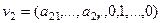
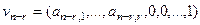
Данная система линейно независима, так как объединяя их в матрицу, увидим, что в её последних 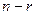столбцах будет минор, устроенный как единичная матрица 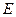, т.е. заведомо ненулевой, равный 1.

2) Докажем, что любое другое решение будет их линейной комбинацией. Рассмотрим последние 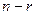координат произвольного решения.

Пусть 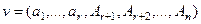- решение однородной системы.

Линейная комбинация решений:

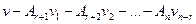тоже является решением.

Но на последних n-r местах она содержит 0, а числа, отличные от 0 на первых r местах. Но тогда первые r столбцов образовали бы ЛЗС – было бы противоречие. Тогда единственная возможность: 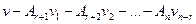нулевой вектор.

Тогда 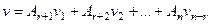, то есть новое решение можно представить в виде такой линейной комбинации ранее найденных 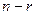решений.

Таким образом, существует не меньше, но и не больше, чем 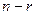различных линейно-независимых решений.

Определение. Данная система, состоящая из 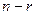линейно-независимых решений, называется фундаментальной системой решений (ФСР) однородной системы уравнений.

Пример. ( 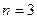, 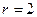). Решить однородную систему:

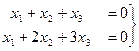
Решение.Если преобразовывать расширенную матрицу, то получим:

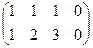
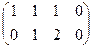
Видим, что справа всё равно как был, так и остаётся столбец из нулей, так что в будущем для однородных систем можно использовать только основную матрицу, ведь расширенная не несёт никакой новой информации, всё равно там справа нулевой столбец, и он не меняется при преобразованиях строк.

Итак, получили систему 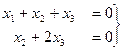базисный минор можно заметить в первых двух столбцах, так что 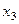свободная переменная, переносим её вправо: 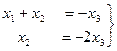. Теперь последовательно выражаем через свободную переменную две базисные переменные.

Из 2-го: 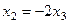, а подставляя в 1-е, получим

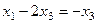, т.е. .

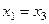Общее решение системы : .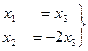

Также записывается в виде вектора: .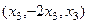

Частные решения: 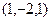, , 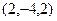, 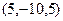и т.д.

То есть все тройки чисел будут пропорциональны какой-то одной.

ФСР (фундаментальная система решений). ФСР состоит из одного вектора .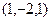

Ответ.Общее решение 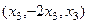, ФСР .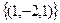

Пример. ( 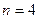, 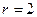). Решить систему уравнений:

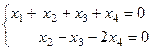
Базисный минор порядка 2 можно найти в левом углу, тогда считаем, что 3-я и 4-я переменная - свободные. Перенесём их через знак равенства. .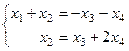

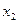уже фактически выражено: 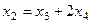, подставим это в первое уравнение, чтобы выразить .

.

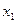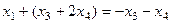
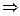
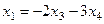Общее решение: { , }.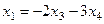

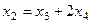Если поочерёдно присвоить значение 1 каждой из свободных переменных (а другая в это время 0) то получим гарантированно 2 линейно-независимых вектора, они не пропорциональны, так как 1 на разных местах.

.

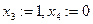
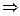
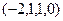
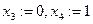
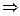
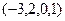Эти 2 вектора { 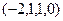, 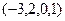} и есть ФСР. Это 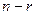частных решений, из которых можно составить любые другие частные решения: любые их линейные комбинации будут частными решениями однородной системы.

Например, их сумма 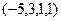также является решением системы.

Примечание.При решении системы в прошлой задаче, со следующей стадии: 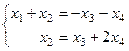может использоваться и метод Крамера.

= .

= .

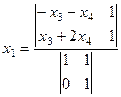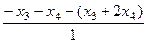
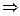
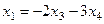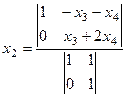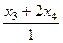
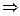
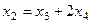* Для системы с квадратной матрицей справа были только числа, для системы с прямоугольной матрицей к ним добавляются свободные переменные, и там будут выражения типа 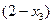. А для однородной системы справа констант нет (они 0), но туда перенесены свободные переменные. Т.е. решение методом Гаусса во всех этих 3 параграфах выполняется похожим образом, только справа разные типы объектов.