Однородные системы линейных уравнений.

Если в каждом уравнении правая часть 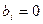, такая система называется однородной.

Расширенная матрица содержит столбец, состоящий только из 0, то есть ранг расширенной матриц точно не больше, чем ранг основной! По теореме Кронекера-Капелли получается, что однородная система всегда совместна, то есть существует хотя бы одно решение.

Заметим, что при подстановке всех 0 вместо неизвестных, 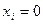, все равенства автоматически выполняются, т.е. нулевое решение для такой системы всегда существует. Оно называется тривиальным решением. Тривиальное решение может быть не единственным, возможно, есть ещё какие-то наборы чисел, которые можно подставить в систему. Основной задачей для однородных систем как раз и является поиск ненулевых решений.

Нетривиальные решения есть, например:

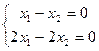решения (1,1), (2,2), и т.д.

Любое (С,С) для 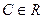есть решение.

Здесь ранг равен 1, и 2-я переменная свободная.

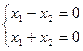А здесь ранг основной матрицы равен 2. 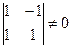, базисный минор фактически заполняет всю основную матрицу, до правого края, в этом случае нет свободных переменных. Решение только тривиальное.

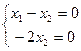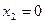Если решать методом Гаусса, то получим тогда , и отсюда 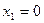. После приведения к треугольному виду, последняя неизвестная получится 0, за ней и предпоследняя и т.д. Если матрица невырожденная, то решение единственно, но поскольку обязательно существует тривиальное, то единственное оно и есть тривиальное (все нули), других решений нет. Итак, сформулируем обнаруженный нами факт в виде теоремы:

Теорема 1.

1) Система линейных однородных уравнений имеет нетривиальные решения .

2) Система линейных однородных уравнений с квадратной основной матрицей 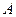имеет нетривиальные решения .

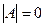Доказательство.

Система имеет решение, отличное от нуля для столбцов основной матрицы выполняется равенство 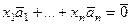при некотором наборе ненулевых коэффициентов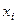 система 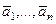является линейно зависимой ранг системы векторов строго меньше 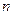ранг матрицы 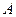строго меньше .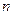

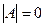Итак, однородная система с квадратной основной матрицей имеет нетривиальные решения тогда и только тогда, когда основная матрица вырожденная.

Следствия из теоремы о наложении решений:

Теорема 2. Линейная комбинация решений однородной системы тоже является решением (множество решений образует линейное пространство).

Доказательство. Дано 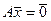, , 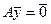тогда .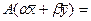

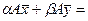
Теорема 3. Сумма решений неоднородной и соответствующей однородной системы есть решение неоднородной системы.

Доказательство.Пусть 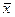решение неоднородной системы, 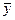- решение соответствующей однородной системы (с той же основной матрицей, но 0 в правой части).

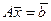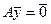, , тогда .

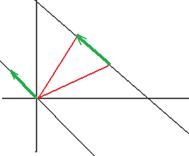
Следствие. Разность двух различных частных решений неоднородной системы есть решение соответствующей однородной системы.

Геометрический смысл. Если взять разность двух радиус-векторов, проведённых к точкам какой-либо прямой, не проходящей через начало координат, получится вектор, лежащий на параллельной прямой, проходящей через начало координат.