Интервальный вариационный ряд.
При большом объеме выборки или если изучаемая величина является непрерывной, ее элементы объединяют в группы (интервалы), представляя результаты опытов в виде группированного (интервального) статистического ряда.
Для построения интервального вариационного ряда необходимо выполнить последовательно следующие действия:
1. определить количество частичных интервалов;
Приблизительно число интервалов 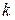 можно оценить исходя только из объема выборки
можно оценить исходя только из объема выборки 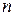 одним из следующих способов:
одним из следующих способов:
А) по формуле Стерджесса:  ;
;
Б) с помощью таблицы:
Объем выборки, 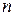
| 25-40 | 40-60 | 60-100 | 100-200 | Больше 200 |
Число интервалов, 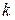
| 5-6 | 6-8 | 7-10 | 8-12 | 10-15 |
2. определить ширину частичных интервалов;
Обычно предпочтительны интервалы одинаковой ширины. Для определения ширины интервалов 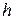 вычисляют:
вычисляют:
· размах варьирования значений выборки 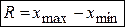 , где
, где 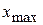 и
и 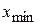 - максимальная и минимальная варианты выборки; затем
- максимальная и минимальная варианты выборки; затем
· длина каждого из частичных интервалов 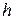 определяют по формуле
определяют по формуле
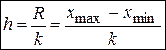 .
.
где 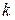 - количество выбранных вами интервалов (от 7 до 15, см. табличку выше).
- количество выбранных вами интервалов (от 7 до 15, см. табличку выше).
3. установить для каждого интервала его верхнюю и нижнюю границы;
Начало первого интервала – это 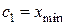 , а конец
, а конец 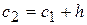 (это будет одновременно и началом второго интервала) и так далее.
(это будет одновременно и началом второго интервала) и так далее.
Условимся все интервалы 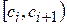 считать с открытым правым концом. Построение интервалов заканчивается, если в интервал попало наибольше значение признака
считать с открытым правым концом. Построение интервалов заканчивается, если в интервал попало наибольше значение признака 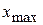 .
.
4. вычислить частоты результатов наблюдений в каждом интервале.
Частоты – это количество 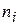 элементов выборки, попавших в каждый интервал. Заметим, что элемент, совпадающий с верхней границей интервала, относится к этому интервалу.
элементов выборки, попавших в каждый интервал. Заметим, что элемент, совпадающий с верхней границей интервала, относится к этому интервалу.
Наряду с частотами подсчитываются также относительные частоты 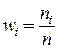 .
.
Полученные результаты действий сводятся в таблицу 2.
Таблица 2. Интервальный вариационный ряд
Номер интервала 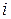
| Интервалы | Середины частичных интервалов
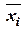
| Частоты
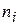
| Относительные частоты
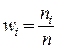
|
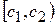
| 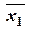
| 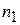
| 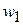
| |
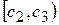
| 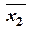
| 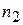
| 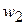
| |
| … | … | … | … | … |
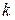
| 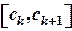
| 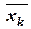
| 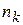
| 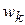
|
| Сумма | - | - | 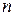
|
Дата добавления: 2020-12-11; просмотров: 483;











