Показательная функция, ее свойства и графики.
Во многих отраслях науки и техники при изучении самых различных явлений и процессов обнаруживается одна общая функциональная зависимость между двумя переменными величинами, участвующими в процессе. Рассмотрим примеры.
Пример 1: С изменением высоты h над уровнем моря атмосферное давление p изменяется по закону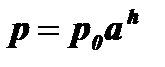 
, где p0 - давление на уровне моря, а - постоянная (const ).
Пример 2: Рост древесины происходит по закону: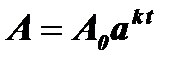 
, где t - время, А0 - начальное количество древесины при t = 0, А - изменяющееся со временем количество древесины, а , k - постоянные (const).
Пример 3: Размножение бактерий в какой-либо культуре происходит по закону: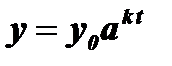 
, где t - время, у0 - начальное количество бактерий при t = 0 , у - изменяющееся со временем количество бактерий, а , k - постоянные (const ).
Пример 4: Распад радия протекает по закону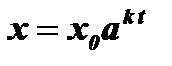 
, где t - время, х0 - начальное количество радия при t = 0, х - изменяющееся со временем количество радия, а , k - постоянные (const).
В приведенных примерах мы имеем дело с процессами, носящими общее название «процессы органического роста». Если отвлечься от физического смысла переменных, участвующих в процессах органического роста и обозначить их х и у, то получим формулу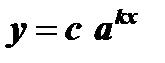 
, где с , а , k - постоянные (const). Мы рассмотрим простейший случай: 
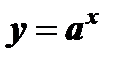, с = k = 1 .
Определение: Функция вида 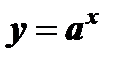, где а > 0, а ¹ 1, называется показательной функцией.
Замечание: При а = 1 функция является постоянной, так как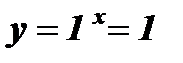 
.
Свойства показательной функции 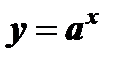, а > 0 , а ¹ 1
1) при 0 < а < 1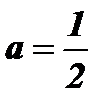 
;
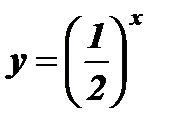2) при а > 1 а = 2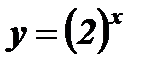 
.
1. Областью определения функции являются все действительные числа, так как положительное число можно возвести в степень с любым действительным показателем: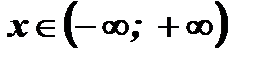 
.
2. Множеством значений функции являются положительные числа, так как при возведении положительного числа в степень с любым действительным показателем получается положительное число: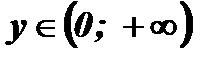 
.
Вывод: График показательной функции расположен в первой и второй координатных четвертях.
3. Функция не является ни четной ни нечетной: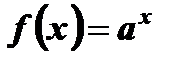 
, 
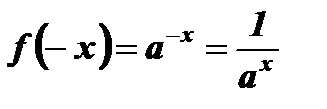, f ( – х)¹ f (х), f ( – х)¹– f ( х).
4. Функция является монотонной:
1) при 0 < а < 1 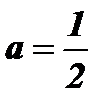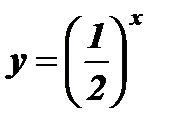– убывающая функция;
2) при а > 1 а = 2 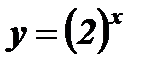– возрастающая функция.
Замечание:
1) При возведении в степень правильной дроби, чем больше показатель степени, тем меньше результат.
2) При возведении в степень числа, большего единицы, чем больше показатель степени, тем больше результат.
Дата добавления: 2016-09-06; просмотров: 1457;
Поиск по сайту
Узнать еще
- V. СПОСОБЫ ПОЛУЧЕНИЯ И ХИМИЧЕСКИЕ СВОЙСТВА АЦЕТИЛЕНОВЫХ И ДИЕНОВЫХ УГЛЕВОДОРОДОВ
- А) кислотные свойства
- А) Логотип и фирменный знак должны создаваться средствами векторной графики.
- А) Основные свойства
- А) Физические свойства минералов
- А. Оптические свойства минералов
- А. Свойства и виды рецепторов. Взаимодействие рецепторов с ферментами и ионными каналами
- Азотная кислота и ее свойства.
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
