Функция является обратимой, так как она монотонна.
6. Нулей функции нет, так как уравнение у = 0 , то есть 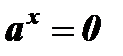 корней не имеет.
корней не имеет.
7. Промежутки знакопостоянства: при 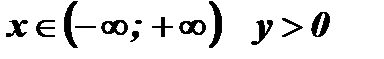 , так как
, так как
при 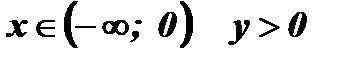
при 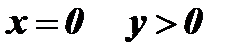
при 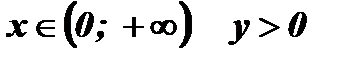
8. Функция ограничена снизу, так как 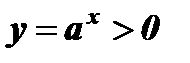 при
при 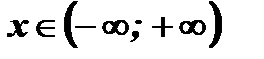 .
.
9. Любая показательная функция проходит через точку (0; 1) , так как при
х = 0 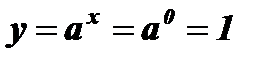 .
.
Замечание:
1) При а > 1функция возрастает тем быстрее, чем больше а;
2) При 0 < а < 1 функция убывает тем быстрее, чем меньше а.
| х |
| у |
| - 3 |
| - 2 |
| - 1 |
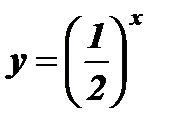
|
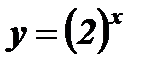
|
0 < а < 1 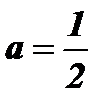
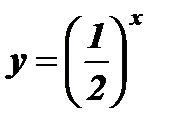
| х | - 3 | - 2 | - 1 | ||||
| у | 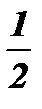
| 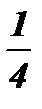
| 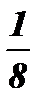
|
а > 1 а = 2 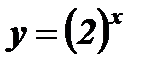
| х | - 3 | - 2 | - 1 | ||||
| у | 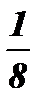
| 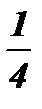
| 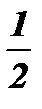
|
Упражнения:
1. Перечислите свойства функции и постройте ее график:
а) 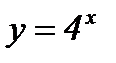 ; б)
; б) 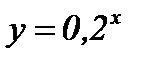 ; в)
; в) 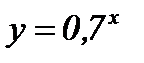 ; г)
; г) 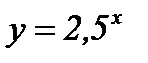 .
.
2. Найдите множество значений функции:
а) 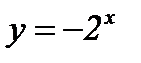 ; б)
; б) 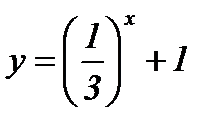 ; в)
; в) 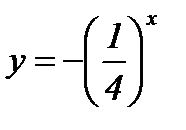 ; г)
; г) 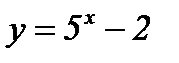 .
.
3. Сравните числа:
а) 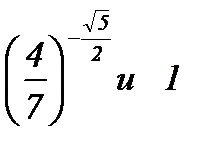 ; б)
; б) 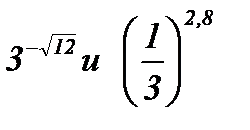 ; в)
; в) 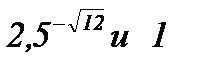 ; г)
; г) 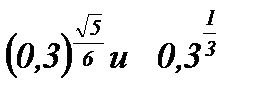 .
.
4. Вычислите:
а) 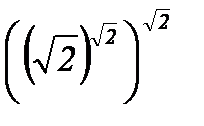 ; б)
; б) 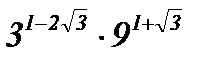 ; в)
; в) 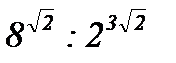 ; г)
; г) 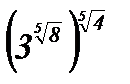 .
.
5. Укажите, какая из данных функций является возрастающей, какая – убывающей на множестве действительных чисел R:
а) 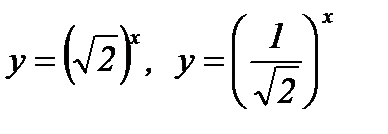 ; б)
; б) 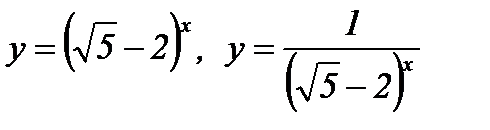 ;
;
в) 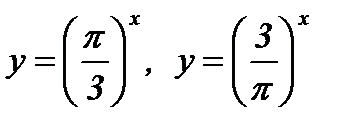 ; г)
; г) 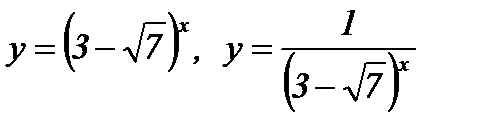 .
.
1. Показательные уравнения.
Определение: Показательными уравнениями называются уравнения, содержащие переменную в показателе степени.
1) 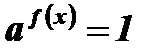 , а > 0 , а ¹ 1
, а > 0 , а ¹ 1
На основании определения степени с нулевым показателем решение уравнения 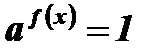 сводится к решению уравнения f(x)=0:
сводится к решению уравнения f(x)=0:
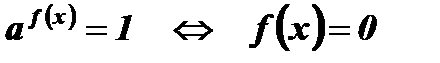 .
.
Пример: Решить уравнение: 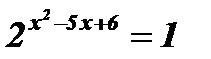 .
.
Решение:
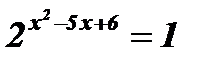 ; 1 = 20;
; 1 = 20; 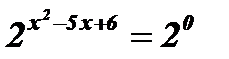 ;
;
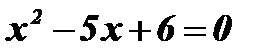 ;
; 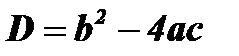 ;
; 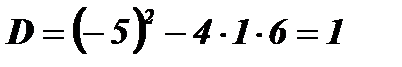 ;
;
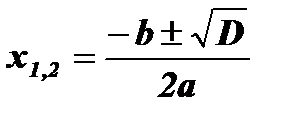 ;
; 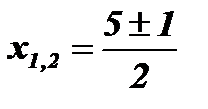 ; х1 = 2; х2 = 3.
; х1 = 2; х2 = 3.
Ответ: х1 = 2; х2 = 3.
Упражнения: Решить уравнение 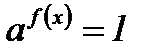 :
:
1. а = 2 f (x)= x2- 40 x + 300;
2. а = 5 f (x)= (x2+ x - 2)(3- x);
3. а = 3 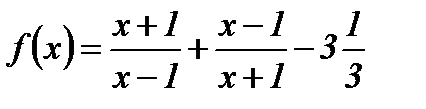 ;
;
4. а = 2 f (x)= x2- 7 x + 12;
5. a = 0,5 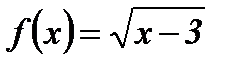 .
.
2) 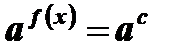 , а > 0 , а ¹ 1
, а > 0 , а ¹ 1
Левая и правая части уравнения 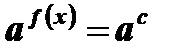 приведены к одному основанию. В этом случае корнями уравнения
приведены к одному основанию. В этом случае корнями уравнения 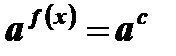 будут корни уравнения
будут корни уравнения 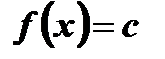 .
.
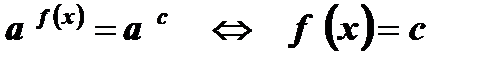 .
.
Пример: Решить уравнения:
1) 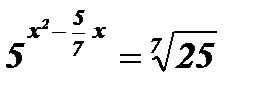 .
.
Решение: 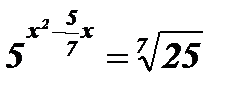 ;
; 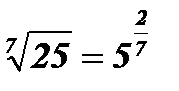 ;
; 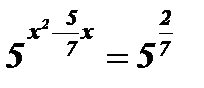 ;
;
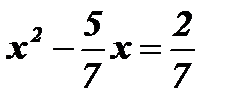 ;
; 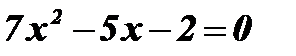 ;
; 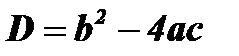 ;
; 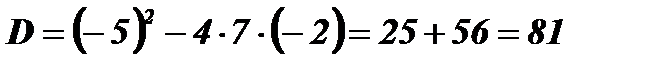 ;
;
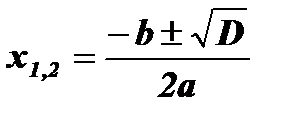 ;
; 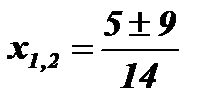 ; х1 =
; х1 = 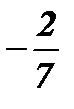 ; х2 = 1.
; х2 = 1.
Ответ: х1 = 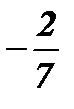 ; х2 = 1.
; х2 = 1.
2) 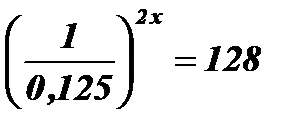 .
.
Решение: 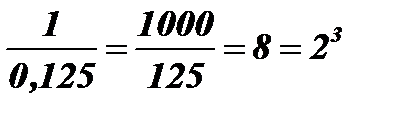 ; 128 = 27;
; 128 = 27;
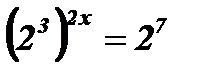 ;
; 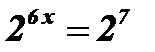 ; 6 х = 7; х =
; 6 х = 7; х = 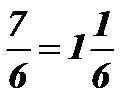 .
.
Ответ: х = 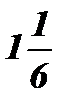 .
.
3) 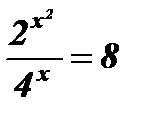 .
.
Решение:
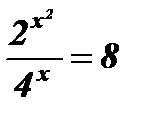 ;
; 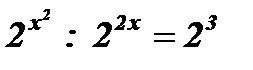 ;
; 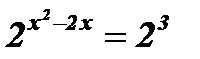 ;
; 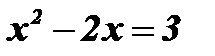 ;
;
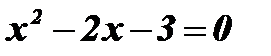 ;
; 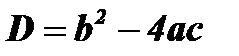 ;
; 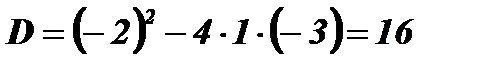 ;
;
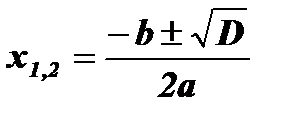 ;
; 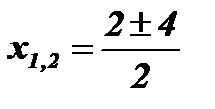 ; х1 = - 1; х2 = 3.
; х1 = - 1; х2 = 3.
Ответ: х1 = - 1; х2 = 3.
Упражнения: Решить уравнения:
1. 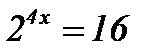 ; ;
| 2. 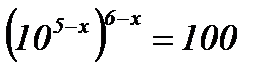 ; ;
|
3. 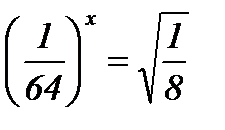 ; ;
| 4. 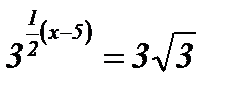 ; ;
|
5. 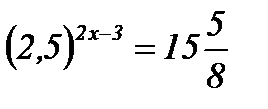 ; ;
| 6. 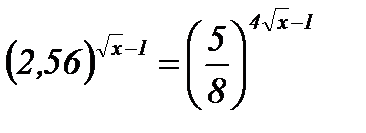 ; ;
|
7. 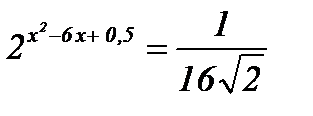 ; ;
| 8. 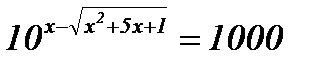 ; ;
|
9. 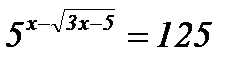 ; ;
| 10. 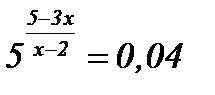 ; ;
|
11. 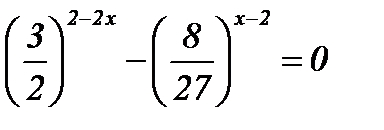 ; ;
| 12. 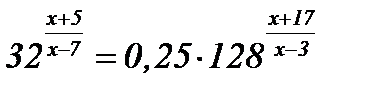 . .
|
3) 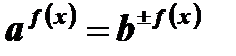 , а > 0 , а ¹ 1 , b > 0 , b ¹ 1 , а ¹ b
, а > 0 , а ¹ 1 , b > 0 , b ¹ 1 , а ¹ b
Уравнение решается делением обеих частей на 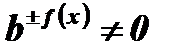 .
.
Пример: Решить уравнения:
1) 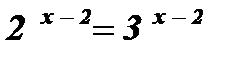 .
.
Решение: Разделим обе части уравнения на 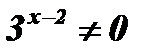 .
.
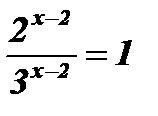 ;
; 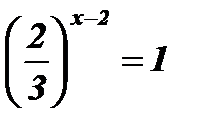 ;
; 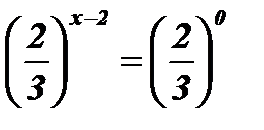 ; х - 2 = 0; х = 2.
; х - 2 = 0; х = 2.
Ответ: х = 2.
2) 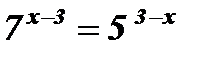 .
.
Решение: 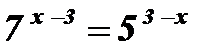 ;
; 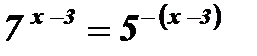 ;
; 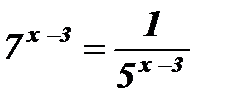 ;
;
Умножим обе части уравнения на 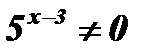 .
.
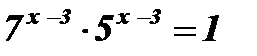 ;
; 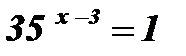 ;
; 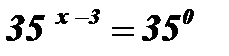 ; х - 3 = 0; х = 3.
; х - 3 = 0; х = 3.
Ответ: х = 3.
Упражнения: Решить уравнения:
1) 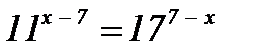 ; ;
| 2) 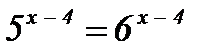 ; ;
|
3) 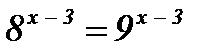 ; ;
| 4) 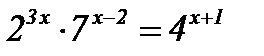 ; ;
|
5) 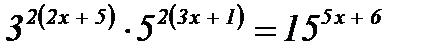 ; ;
| 6) 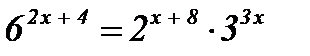 . .
|
4) 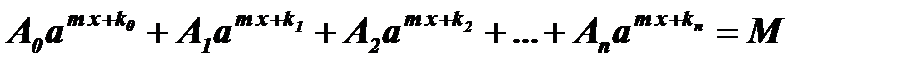 , а > 0 , а ¹ 1
, а > 0 , а ¹ 1
Особенностью уравнения является наличие одного и того же коэффициента перед х. Для решения этого уравнения выносят за скобки общий множитель 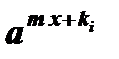 , где k i - наименьшее из чисел k0 , k1 , k2 , … , kп .
, где k i - наименьшее из чисел k0 , k1 , k2 , … , kп .
Пример:
1) 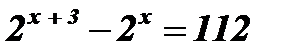 .
.
Решение: 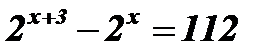 ;
; 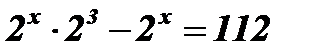 ;
; 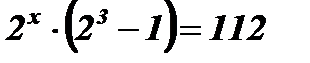 ;
; 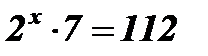 ;
; 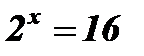 ;
; 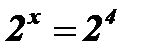 ; х = 4.
; х = 4.
Ответ: х = 4.
2) 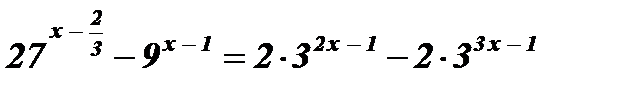 .
.
Решение:
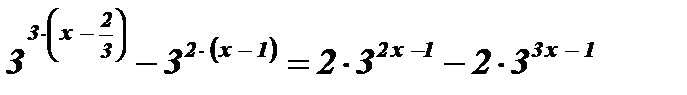 ;
; 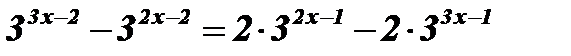 ;
;
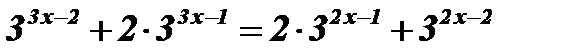 ;
; 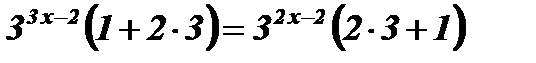 ;
;
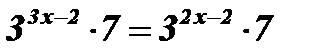 ;
; 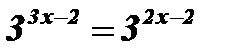 ; 3х - 2 = 2х - 2; 3х - 2х = 2 - 2; х = 0.
; 3х - 2 = 2х - 2; 3х - 2х = 2 - 2; х = 0.
Ответ: х = 0.
3) 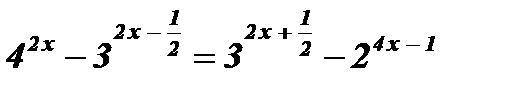 .
.
Решение:
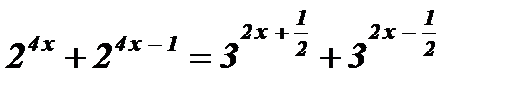 ;
; 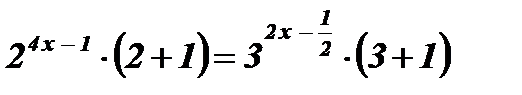 ;
;
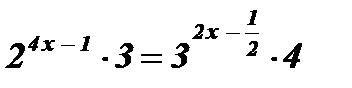 ;
; 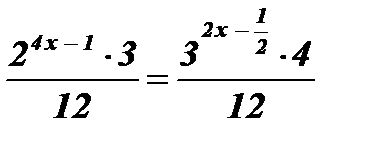 ;
; 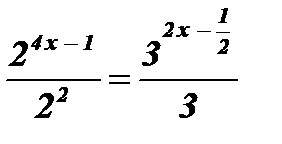 ;
;
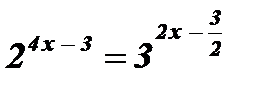 ;
; 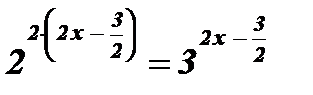 ;
; 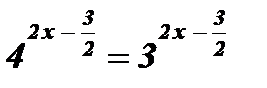 ;
;
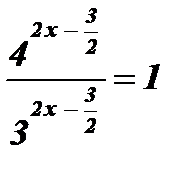 ;
; 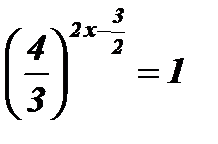 ;
; 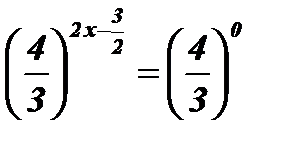 ;
; 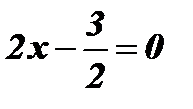 ;
; 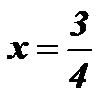 .
.
Ответ: 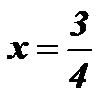 .
.
Упражнения: Решить уравнения:
1) 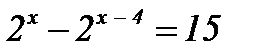 ; ;
| 2) 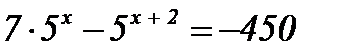 ; ;
|
3) 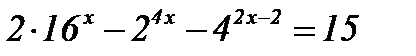 ; ;
| 4) 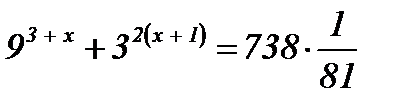 ; ;
|
5) 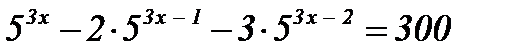 ; ;
| 6) 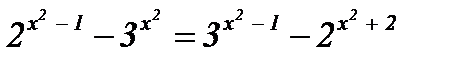 ; ;
|
5) 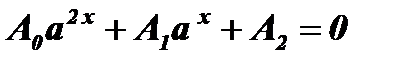 , а > 0 , а ¹ 1
, а > 0 , а ¹ 1
Уравнение 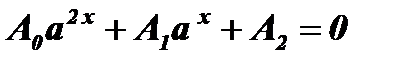 с помощью подстановки
с помощью подстановки 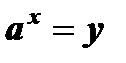 обращается в квадратное уравнение:
обращается в квадратное уравнение: 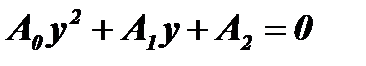 . Решив квадратное уравнение, найдем у1, у2 . После этого решение уравнения
. Решив квадратное уравнение, найдем у1, у2 . После этого решение уравнения 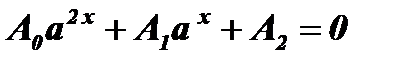 сводится к решениюдвух уравнений:
сводится к решениюдвух уравнений: 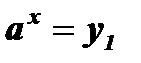 ,
, 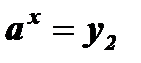 .
.
Пример:
1) 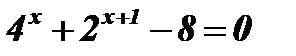 .
.
Решение: 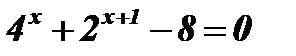 ;
; 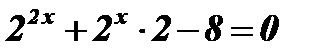 ;
; 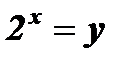 ;
;
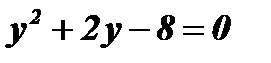 ;
; 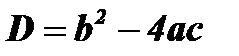 ;
; 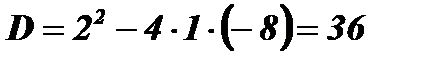 ;
;
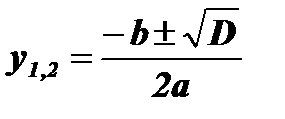 ;
; 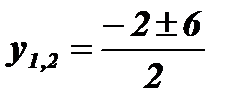 ; у1 = - 4; у2 = 2;
; у1 = - 4; у2 = 2;
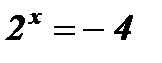 - уравнение корней не имеет, так как
- уравнение корней не имеет, так как 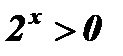 ;
;
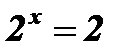 ; х = 1.
; х = 1.
Ответ: х = 1.
2) 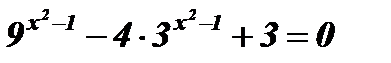 .
.
Решение:
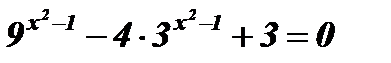 ;
; 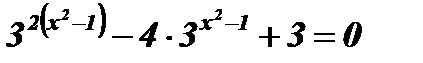 ;
; 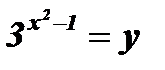 ;
;
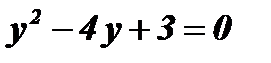 ;
; 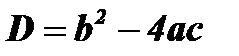 ;
; 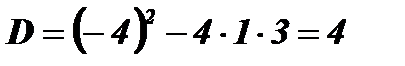 ;
;
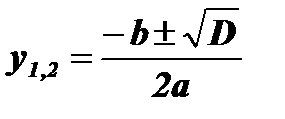 ;
; 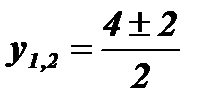 ; у1 = 1; у2 = 3;
; у1 = 1; у2 = 3;
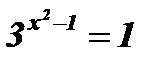 ; х2 - 1 = 0; х2 = 1; х1 = - 1; х2 = 1;
; х2 - 1 = 0; х2 = 1; х1 = - 1; х2 = 1;
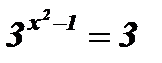 ; х2 - 1 = 1; х2 = 2; х3 =
; х2 - 1 = 1; х2 = 2; х3 = 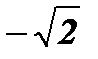 ; х4 =
; х4 = 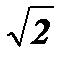 .
.
Ответ: х1 = - 1; х2 = 1; х3 = 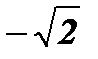 ; х4 =
; х4 = 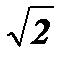 .
.
Упражнения: Решить уравнения:
1) 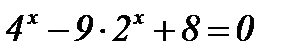 ; ;
| 2) 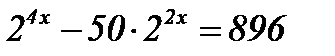 ; ;
|
3) 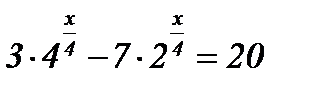 ; ;
| 4) 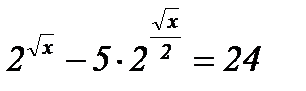 ; ;
|
5) 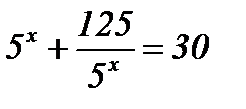 ; ;
| 6) 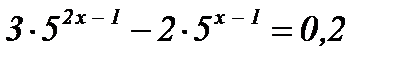 ; ;
|
7) 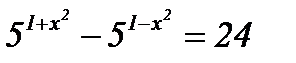 . .
|
6) 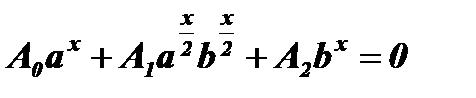 , а > 0 , а ¹ 1, b > 0 , b ¹ 1.
, а > 0 , а ¹ 1, b > 0 , b ¹ 1.
Отметим, что в выражении 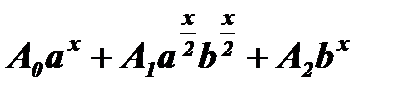 показатели степеней в первом и третьем слагаемых вдвое больше показателей степеней во втором слагаемом. Такие выражения называются однородными 2-ого порядка. А уравнения вида
показатели степеней в первом и третьем слагаемых вдвое больше показателей степеней во втором слагаемом. Такие выражения называются однородными 2-ого порядка. А уравнения вида 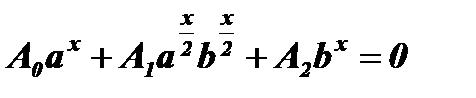 называются однородными 2-ого порядка. Разделив уравнение на
называются однородными 2-ого порядка. Разделив уравнение на 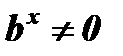 , получим:
, получим: 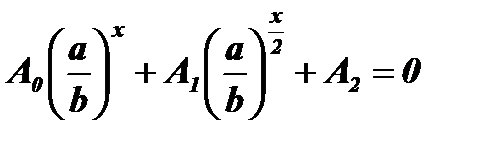 .
.
Уравнение 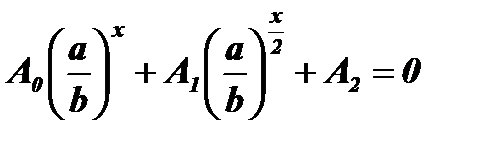 с помощью подстановки
с помощью подстановки 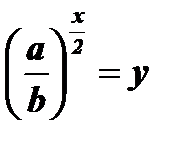 обращается в квадратное уравнение:
обращается в квадратное уравнение: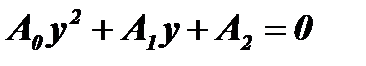 . Решив квадратное уравнение, найдем у1, у2 и, возвращаясь к первоначальной переменной, получим два уравнения
. Решив квадратное уравнение, найдем у1, у2 и, возвращаясь к первоначальной переменной, получим два уравнения 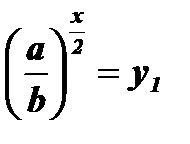 и
и 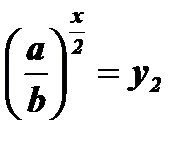 .
.
Пример: 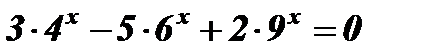 .
.
Решение: 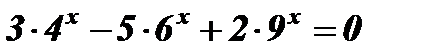 ;
; 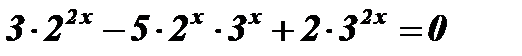 ;
;
Разделим обе части уравнения на 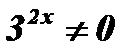 :
:
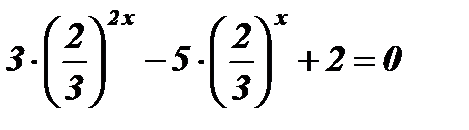 ;
; 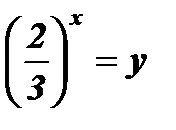 ;
;
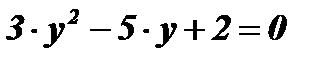 ;
; 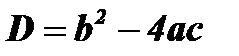 ;
; 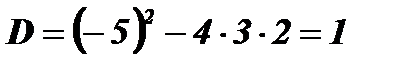 ;
;
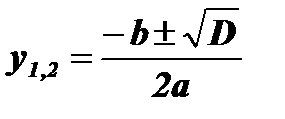 ;
; 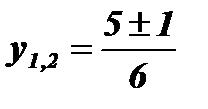 ; у1 =
; у1 = 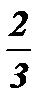 ; у2 = 1;
; у2 = 1;
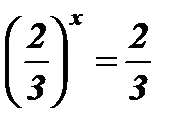 ; х1 = 1;
; х1 = 1; 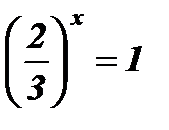 ; х2 = 0.
; х2 = 0.
Ответ: х1 = 1; х2 = 0 .
Упражнения: Решить уравнения:
1) 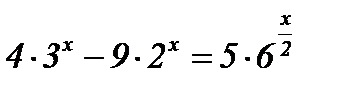 ; ;
| 2) 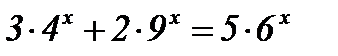 ; ;
|
3) 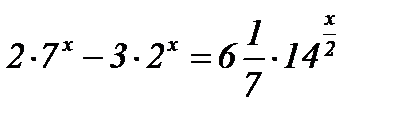 ; ;
| 4) 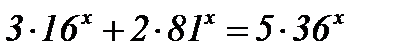 . .
|
Дата добавления: 2016-09-06; просмотров: 1604;











