Проверка: Все корни принадлежат области определения уравнения.
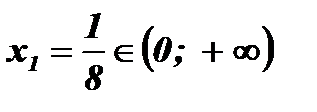 ;
; 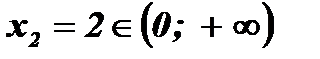 .
.
Ответ: х1 = 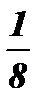 ; х2 = 2.
; х2 = 2.
Упражнения: Решить уравнения:
|
|
|
|
|
|
7. Формула для перехода от одной системы логарифмов к другой.
Очень часто в математике встает задача нахождения логарифма положительного числа b по основанию n (n > 0, n ¹ 1), если известен логарифм этого числа по другому основанию а (а > 0, a ¹ 1). Задача сводится к нахождению переводного множителя, с помощью которого осуществляется переход от одной системы логарифмов к другой.
Задача:
Дано:
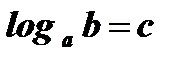 ;
;
Найти:
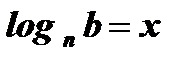 .
.
Решение:
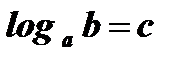 Û
Û 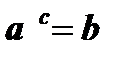 ;
;
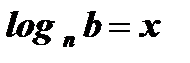 Û
Û 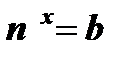 ;
;
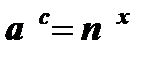
Прологарифмируем обе части равенства по основанию а:
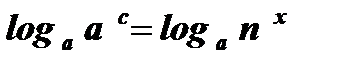 Û
Û 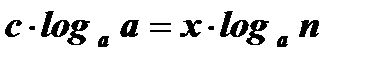 Û
Û 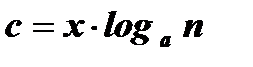 Û
Û
Û 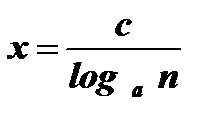 Û
Û 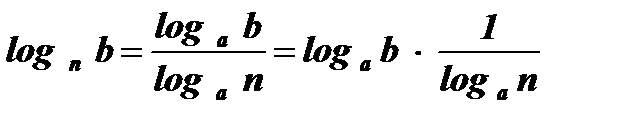 .
.
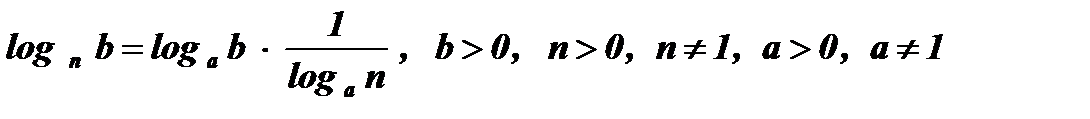 .
.
Пример:
-
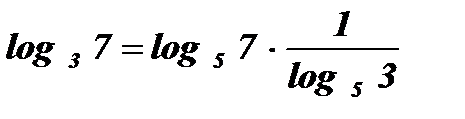 ;
; -
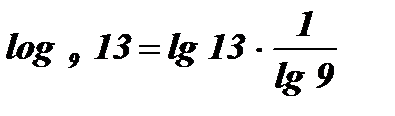 .
.
Вывод:
1. Выражение 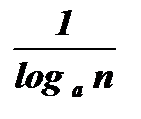 называется модулем перехода от одной системы логарифмов к другой. Равенство
называется модулем перехода от одной системы логарифмов к другой. Равенство 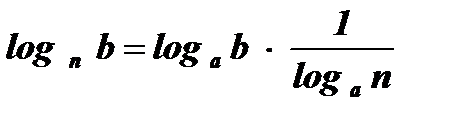 называется формулой перехода от одной системы логарифмов к другой.
называется формулой перехода от одной системы логарифмов к другой.
Замечание: Формула 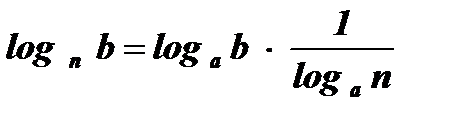 дополняет уже известные свойства логарифмов (пункт № 16).
дополняет уже известные свойства логарифмов (пункт № 16).
2. Логарифм числа при данном основании равен логарифму этого же числа при другом основании, умноженному на модуль перехода.
3. Если а = b ,то 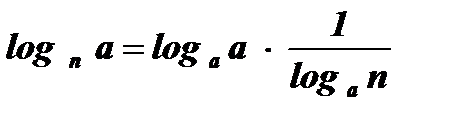 или
или 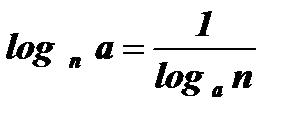 , то есть
, то есть 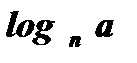 и
и 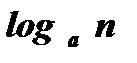 являются взаимно обратными числами.
являются взаимно обратными числами.
Замечание: Формула 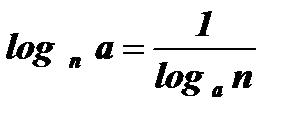 дополняет уже известные свойства логарифмов (пункт № 16).
дополняет уже известные свойства логарифмов (пункт № 16).
4. 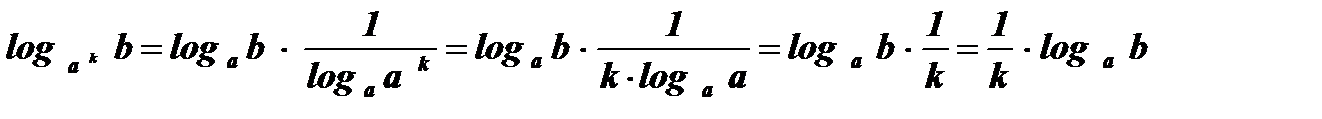 ;
;
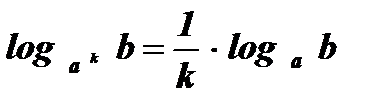 .
.
Замечание: Формула 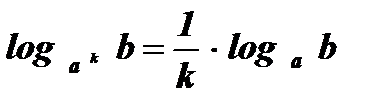 дополняет уже известные свойства логарифмов (пункт № 16).
дополняет уже известные свойства логарифмов (пункт № 16).
Пример: 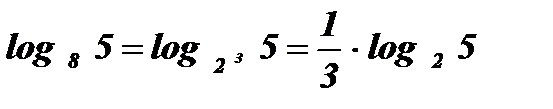 .
.
Рассмотрим примеры решения логарифмических уравнений с использованием формулы перехода от одной системы логарифмов к другой.
Пример:
-
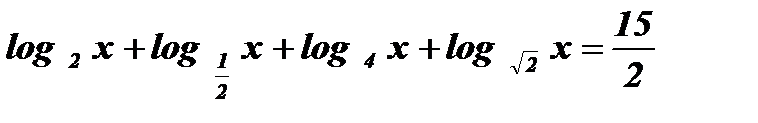 .
.
Решение:
Найдем область определения уравнения, используя определение логарифма:
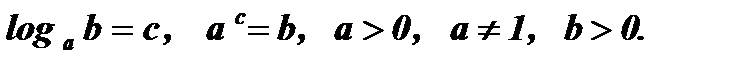
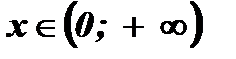 .
.
Используя формулу перехода от одной системы логарифмов к другой 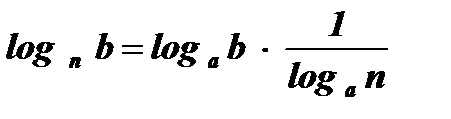 приведем логарифмы к основанию 2:
приведем логарифмы к основанию 2:
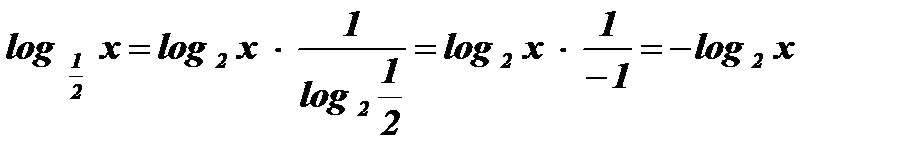 ;
;
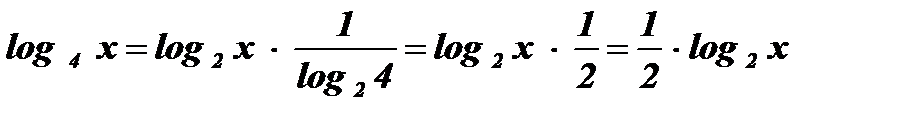 ;
;
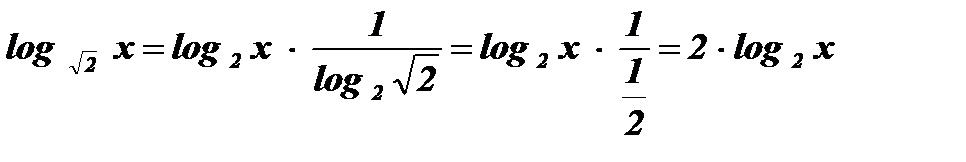 ;
;
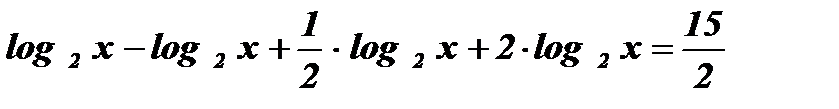 ;
;
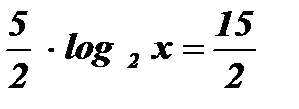 ;
; 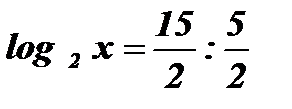 ;
; 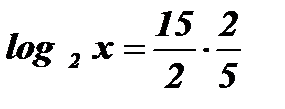 ;
; 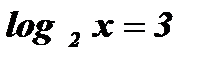 ;
;
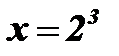 ; х = 8 .
; х = 8 .
Проверка:
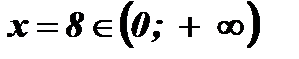 .
.
Ответ: х = 8 .
-
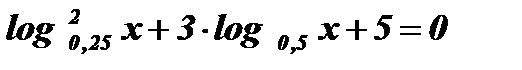 .
.
Решение:
Найдем область определения уравнения, используя определение логарифма:
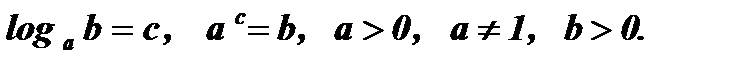
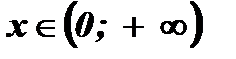 .
.
Используя формулу перехода от одной системы логарифмов к другой 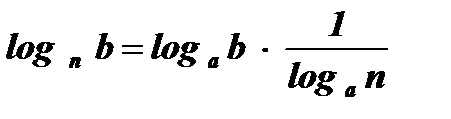 приведем логарифмы к основанию 2:
приведем логарифмы к основанию 2:
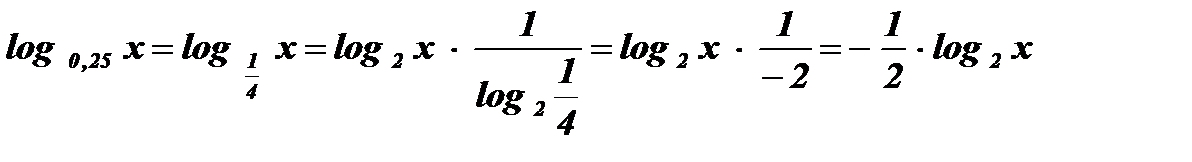 ;
;
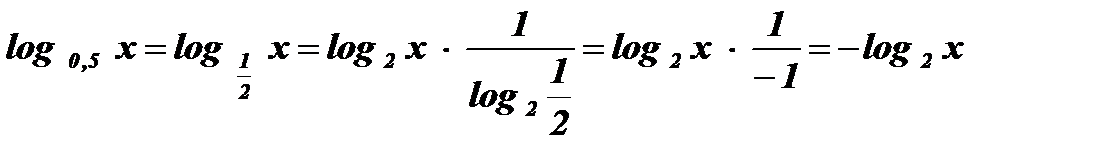 ;
;
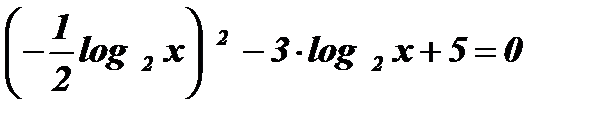 ;
;
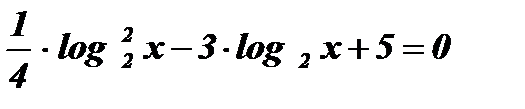 ;
;
Умножим обе части уравнения на 4:
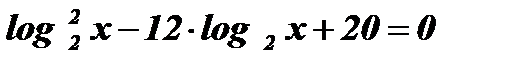 ;
;
Введем новую переменную: 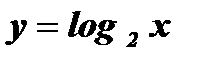 ;
;
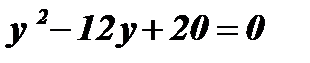 ;
; 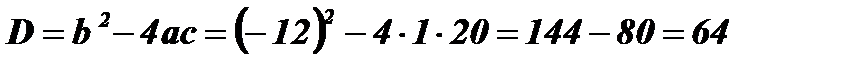 ;
;
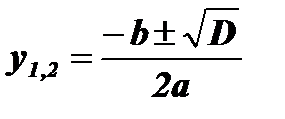 ;
; 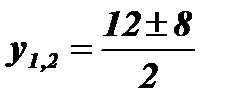 ; у1 = 2; у2 = 10;
; у1 = 2; у2 = 10;
у1 = 2 ; lоg2 x = 2; х1 = 4;
у2 = 10; lоg2 x = 10; х2 = 1024.
Проверка:
Все корни принадлежат области определения уравнения.
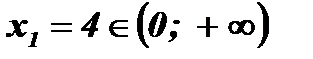 ;
; 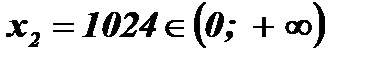 .
.
Ответ: х1 = 4; х2 = 1024.
Упражнения: Решить уравнения:
-
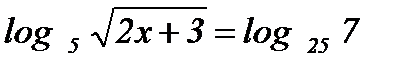 ;
; -
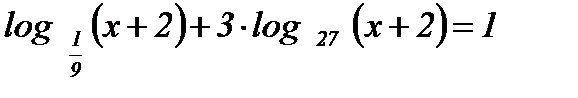 ;
; -
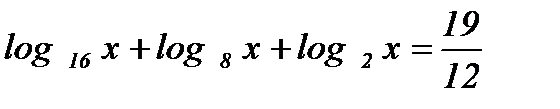 ;
; -
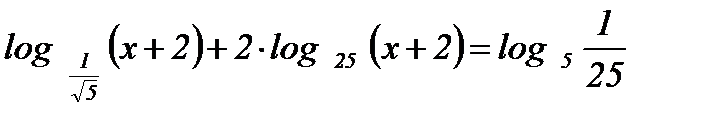 ;
; -
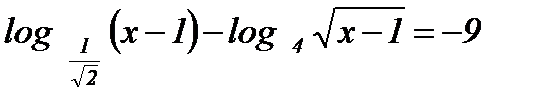 .
.
8. Логарифмические неравенства.
Решение логарифмических неравенств основано на том, что функция 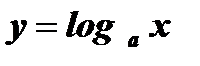 при а > 1 является монотонно возрастающей, а при 0 < а < 1 - монотонно убывающей.
при а > 1 является монотонно возрастающей, а при 0 < а < 1 - монотонно убывающей.
Пример: Решить логарифмические неравенства:
1. 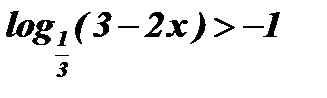 .
.
2. 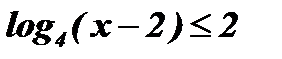 .
.
3. 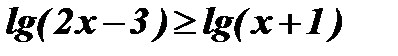 .
.
4. 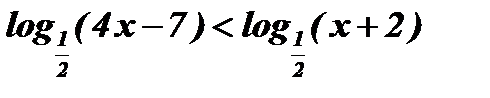 .
.
1. 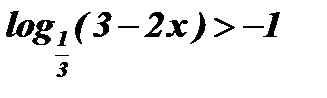 .
.
Решение:
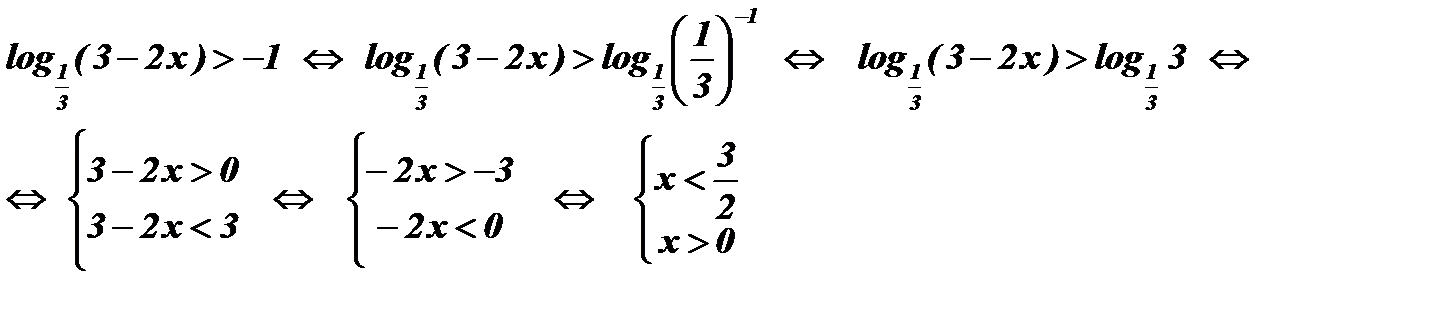 Ответ:
Ответ: 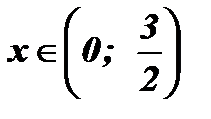 .
.
2. 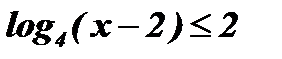 .
.
Решение:
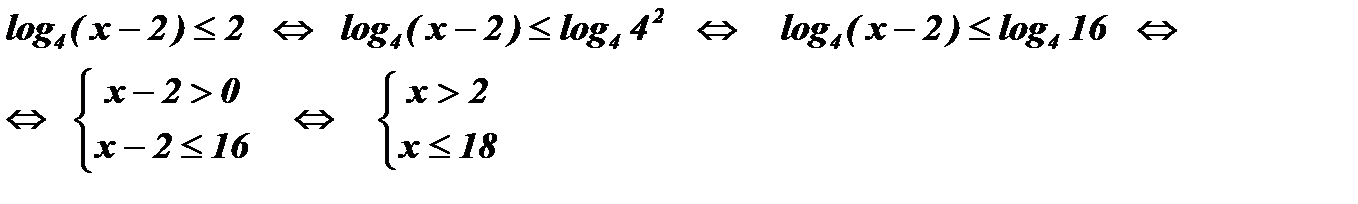
Ответ: 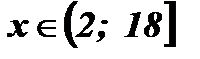 .
.
3. 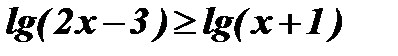 .
.
Решение:
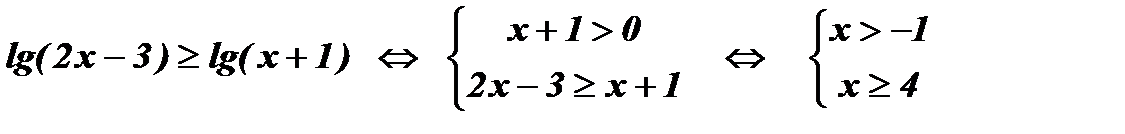
Ответ: 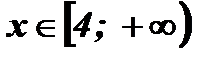 .
.
4. 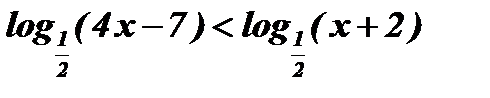 .
.
Решение:
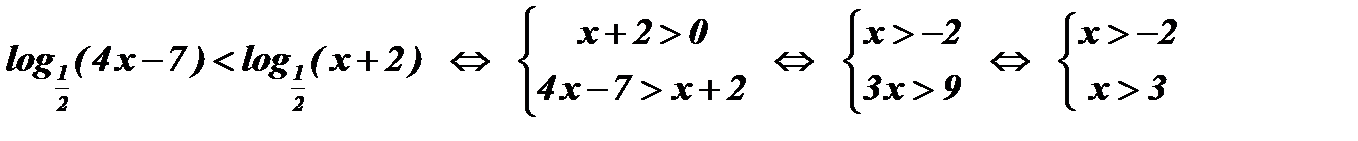
Ответ: 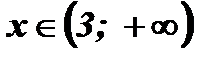 .
.
1.
Дата добавления: 2016-09-06; просмотров: 1527;

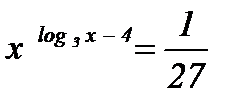 ;
;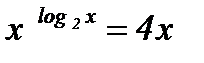 ;
;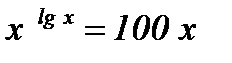 ;
;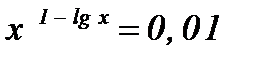 ;
;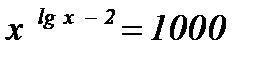 ;
;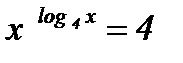 ;
;









