Проверка согласованности оценок для сравниваемых объектов.
Определив вектор приоритетов, можно найти главное собственное значение матрицы суждений  , которое используется для оценки согласованности, отражающей пропорциональность предпочтений. Чем ближе
, которое используется для оценки согласованности, отражающей пропорциональность предпочтений. Чем ближе  к размерности матрицы суждений
к размерности матрицы суждений 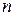 , тем более согласован результат. Главное собственное значение матрицы парных сравнений представляет собой сумму отклонений оценок парных сравнений от идеального значения (в частном случае, когда отклонения равны нулю, главное значение матрицы будет равно количеству сравниваемых объектов). Отклонения (рассогласование с идеальным значением) оценок парных сравнений от идеального значения вычисляется как произведение нормализованной оценки для каждого объекта на суммарное значение оценок для рассматриваемого объекта, выставленных экспертом (сумма оценок по столбцу матрицы парных сравнений). Вычисление
, тем более согласован результат. Главное собственное значение матрицы парных сравнений представляет собой сумму отклонений оценок парных сравнений от идеального значения (в частном случае, когда отклонения равны нулю, главное значение матрицы будет равно количеству сравниваемых объектов). Отклонения (рассогласование с идеальным значением) оценок парных сравнений от идеального значения вычисляется как произведение нормализованной оценки для каждого объекта на суммарное значение оценок для рассматриваемого объекта, выставленных экспертом (сумма оценок по столбцу матрицы парных сравнений). Вычисление  осуществляется по следующей формуле:
осуществляется по следующей формуле:
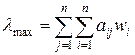 , ,
| (6.20) |
где 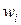 значение нормализованной оценки для i – го объекта (номер строки),
значение нормализованной оценки для i – го объекта (номер строки), 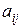 - значение оценки парного сравнения объекта i с объектом j (элементы выбираются по столбцам матрицы парных сравнений).
- значение оценки парного сравнения объекта i с объектом j (элементы выбираются по столбцам матрицы парных сравнений). 
При парном сравнении объектов необходимо выставить оценку, которая показывает величину - на сколько, один объект предпочтительнее другого. Эксперт может ошибиться при сравнении другой пары объектов, что приведет к противоречивости результатов. Специалисты по логике исследуют причины противоречий в суждениях экспертов и дают рекомендации по разрешению конфликтных ситуаций. Тем не менее, в качестве парадокса можно показать пример, как можно «заблудиться в трех соснах». Имеется в виду следующее высказывание: «отдыхать лучше с друзьями на рыбалке (рыбалка), а не дома (дом), хотя охотиться (охота) лучше, чем ловить рыбу, но вместо охоты лучше всего находиться дома». Если построить граф, состоящий из трех вершин (рыбалка, дом, охота), и показать дугами на графе предпочтения, то получится замкнутая петля, т.е. будет вариант, когда появится состояние неопределенности варианта при выборе решения, что показано на рис. 11.
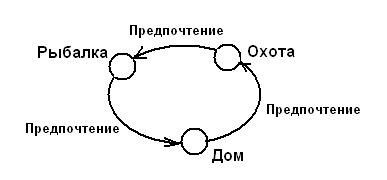
Рис. 11. Демонстрация состояния неопределенности варианта при выборе решения
Для выявления противоречивости результатов, которые предложил эксперт при заполнении матрицы парных сравнений используется количественная оценка – индекс согласованности (ИС). Индекс согласованности – количественная оценка противоречивости результатов сравнений (для системы в целом, для узлов одного кластера или для кластеров, имеющих общую вершину), который дает информацию о степени нарушения согласованности. Вместе с матрицей парных сравнений мы имеем меру оценки степени отклонения от согласованности. Если такие отклонения превышают установленные пределы, то тому, кто проводит суждения, следует перепроверить их в матрице. Отклонение от согласованности может быть выражено величиной относительного коэффициента согласованности равного
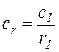 , ,
| (6.21) |
где
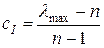 - коэффициент согласованности матрицы - коэффициент согласованности матрицы 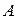 , ,
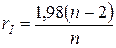 - стохастический коэффициент
согласованности матрицы - стохастический коэффициент
согласованности матрицы 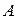 . .
| (6.22) |
Стохастический коэффициент согласованности 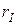 определяется эмпирическим путем как среднее значение коэффициента
определяется эмпирическим путем как среднее значение коэффициента 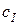 для большой выборки генерированных случайным образом матриц сравнения
для большой выборки генерированных случайным образом матриц сравнения 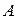 . Коэффициент согласованности
. Коэффициент согласованности 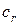 используется для проверки согласованности матрицы сравнения
используется для проверки согласованности матрицы сравнения 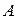 следующим образом. Если
следующим образом. Если 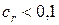 , уровень несогласованности является приемлемым. В противном случае уровень несогласованности матрицы сравнения
, уровень несогласованности является приемлемым. В противном случае уровень несогласованности матрицы сравнения 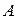 является высоким, и лицу, принимающему решение, рекомендуется проверить элементы парного сравнения
является высоким, и лицу, принимающему решение, рекомендуется проверить элементы парного сравнения 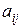 матрицы
матрицы 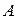 в целях получения более согласованной матрицы.
в целях получения более согласованной матрицы.
Следует иметь в виду, что между достоверностью и непротиворечивостью сравнений нет явной связи. Противоречия в сравнениях возникают из-за субъективных ошибок экспертов. Коэффициент согласованности не зависит от шкал сравнений, но зависит от количества парных сравнений Коэффициент согласованности – положительное число. Чем меньше противоречий в сравнениях, тем меньше значение коэффициента согласованности. При использовании способа сравнений с эталоном значение коэффициента согласованности равно нулю.
Идеальные сравнения – наиболее близкие, к имеющимся, непротиворечивым результатам сравнений. Идеальным сравнениям соответствуют нулевой индекс согласованности и, соответственно, нулевое значение относительной согласованности. Знание идеальных сравнений используется при проведении процедуры согласования для кластеровAdvice_CoordinateKlaster, позволяющей скорректировать сравнения для уменьшения их противоречивости. В качестве подтверждения справедливости теоретических высказываний Т. Саати о величине относительной согласованности оценок, в таблице 33 представлены два варианта вычислений собственных значений матрицы парных сравнений (матрицы суждений), а также приведены обобщенные результаты по коэффициенту согласованности.
Таблица 33.

| 4,2021 | 4,0000 |
Коэффициент согласованности 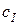
| 0,0674 | 0,0000 |
Относительный коэффициент согласованности 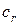
| 7,48% | 0,00% |
6.4. Согласованность мнений группы экспертов.
Метод парных сравнений был рассмотрен применительно к обработке результатов опроса одного эксперта. Индивидуальные экспертные оценки имеют право на существование и даже практическое использование, но уверенность в их объективности очень низкая. Поэтому предпочтение отдают групповым экспертным оценкам. В простейшем случае за групповую оценку принимают усредненное значение индивидуальных оценок. Применение такого способа предполагает, что компетентность экспертов одинакова. Поэтому на основании таблиц парных сравнений 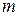 экспертов строится матрица математических ожиданий оценок всех пар объектов как их среднее значение. Затем по этой матрице вычисляется вектор коэффициентов относительной важности объектов (вектор приоритетов). Рассмотрим на примере, как строится матрица попарного сравнения для нескольких экспертов.
экспертов строится матрица математических ожиданий оценок всех пар объектов как их среднее значение. Затем по этой матрице вычисляется вектор коэффициентов относительной важности объектов (вектор приоритетов). Рассмотрим на примере, как строится матрица попарного сравнения для нескольких экспертов.
Пример. Предположим, что в результате опроса трех (m=3) экспертов о степени влияния на результат трех (n=3) различных факторов получены следующие таблицы парных сравнений:
|
|
|
Необходимо получить групповую оценку влияния факторов.
Решение. Для получения групповой оценки степени влияния каждого из факторов на результат, построим матрицу математических ожиданий оценок каждой из пар объектов, которая для рассматриваемого примера будет иметь вид:
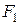
| 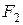
| 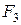
| |
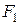
| 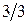
| 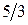
| 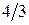
|
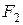
| 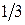
| 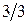
| 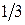
|
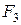
| 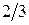
| 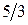
| 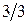
|
Значения элементов этой матрицы получены из следующих выражений:
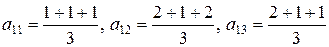 . .
| (6.23) |
Воспользуемся вышеописанным алгоритмом приближенного вычисления собственных векторов матрицы парных сравнений, определим вектор приоритетов для рассматриваемых трех объектов. Для наглядности, каждый из шагов представим в виде:
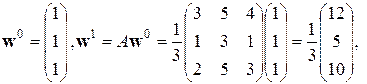
| (6.24) |
Теперь разделим все компоненты на коэффициент нормировки 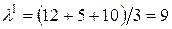 . В результате получаем
. В результате получаем
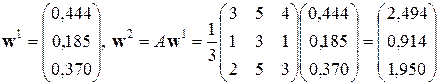 . .
| (6.25) |
Теперь разделим все компоненты на коэффициент нормировки 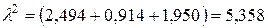 . В результате получаем
. В результате получаем
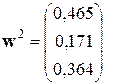 . .
| (6.26) |
Продолжая итерационный процесс до тех пор, пока норма оценки 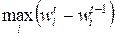
 не будет меньше заданной величины, получим
не будет меньше заданной величины, получим
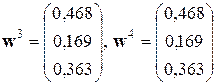 . .
| (6.27) |
На четвертом шаге выполняется условие выхода, что позволяет за групповую оценку степени влияния на результат принять вектор коэффициентов относительной важности объектов вида: 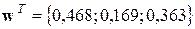 . Таким образом, данные факторы ранжируются как
. Таким образом, данные факторы ранжируются как 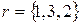 .
.
Дата добавления: 2020-11-18; просмотров: 576;

 )
) 
 )
)  )
) 









