Введение в мир Фибоначчи

Статуя Леонардо Фибоначчи, Пиза, Италия.
Надпись гласит: "A. Leonardo Fibonacci, Insigne
Matematico Piisano del Secolo XII."

ИСТОРИЧЕСКИЕ И МАТЕМАТИЧЕСКИЕ ПРЕДПОСЫЛКИ ЗАКОНА ВОЛН

Последовательность чисел Фибоначчи была открыта (на самом деле, повторно) Леонардо Фибоначчи де Пиза, математиком тринадцатого века (в России известен как Леонардо Пизанский*). Мы обрисуем исторические предпосылки этого удивительного человека и затем более полно обсудим последовательность (формально, это действительно последовательность, а не ряд) чисел, которая носит его имя. Когда Эллиотт писал Закон Природы, он в частности ссылался на последовательность Фибоначчи, как математическую основу Закона волн. Здесь достаточно сказать, что фондовый рынок имеет склонность демонстрировать очертание, которое можно сравнить с фигурой, присутствующей в последовательности Фибоначчи. {Для дальнейшего обсуждения такой математики вне рамок Закона волн см. "Mathematical Basis of Wave Theory" ("Математическая основа волновой теории") Уолтера Уайта (Walter E. White).}

В начале 1200х, Леонардо Фибоначчи из Пизы, Италия, опубликовал свою знаменитую Liber Abacci {Книга абака (Книга вычислений); абак(а) - счеты*}, которая представила Европе одно из величайших открытий всех времен, а именно десятичную систему счисления, включающую положение нуля в качестве первой цифры в записи числового ряда. Эта система, которая включала привычные символы 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, стала известной как Индусско-Арабская система и сейчас используется повсеместно.

С истинной числовой или зависимой от положения цифр системой, подлинное значение, представленное любым символом, помещенным в ряд с другими символами, зависит не только от его основного цифрового значения, но также и от его положения в этом ряду, т.е. 58 имеет отличное от 85 значение. Хотя тысячами лет ранее Вавилонцы и Майя из Центральной Америки независимо друг от друга изобрели числовую или зависимую от положения цифр систему счисления, их методы были неудобными в других отношениях. По этой причине Вавилонская система, которая первая использовала нуль и положение цифр, не вошла ни в греческую, ни даже в римскую системы, чьи нумерации заключали в себе семь символов I, V, X, L, C, D и M с нецифровыми (но числовыми*) значениями присвоенными этим символам. Сложение, вычитание, умножение и деление в системе, использующей эти нецифровые символы, является нелегкой задачей, когда используются большие числа. Пародоксально, но чтобы решить эту проблему римляне использовали очень древний вычислительный прибор, известный как счеты. Так как этот прибор основан на цифрах и содержит в себе нулевой принцип, он действовал в качестве необходимого дополнения к римской вычислительной системе. В течение веков счетоводы и купцы зависили от помощи счет в механике их задач. Фибоначчи, после выражения основного принципа счет в Книге абака, начал использовать свою новую систему во время своих путешествий. Посредством его усилий новая система с ее простым способом вычисления, в конце концов, была передана Европе. Постепенно старое использование римских цифр было заменено арабской цифровой системой. Введение новой системы в Европу было первым важным достижением в области математики с момента падения Рима более семи веков назад. Фибоначчи не только сохранил математику в Средневековье, но и заложил основу длительной эволюции в области высшей математики и связанных областях физики, астрономии и машиностроения. Хотя мир позже почти потерял Фибоначчи из вида, он, несомненно, был человеком своего времени. Его известность была таковой, что Фредерик II, естествоиспытатель и ученый по праву, разыскал его, организовав поездку в Пизу. Фредерик II был Императором Священного Рима, Королем Сицилии и Иерусалима, потомком двух самых знатных семей в Европе и Сицилии и наиболее могущественным правителем своего времени. Его стремлением была абсолютная монархия, и он окружал себя со всей помпой Римского императора.

Встреча между Фибоначчи и Фредериком II произошла в 1225 году и была событием большой важности для города Пизы. Император ехал верхом во главе длинной процессии трубачей, придворных, рыцарей, чиновников и бродячего зверинца животных. Некоторые проблемы, которые Император поставил перед знаменитым математиком, подробно изложены в Книге абака. Фибоначчи, очевидно, решил проблемы, поставленные Императором, и навсегда стал желанным гостем при Королевском дворе. Когда Фибоначчи перерабатывал Книгу абака в 1228 году, он посвятил исправленную редакцию Фредерику II.

Будет почти преуменьшением, если сказать, что Леонардо Фибоначчи был величайшим математиком Средневековья. Всего он написал три значительных математических труда: Книга абака, опубликованная в 1202 году и переизданная в 1228 году, Практическая геометрия, опубликованная в 1220 году, и Книга квадратур. Как указано в документах 1240 года, восхищенные граждане Пизы говорили, что он был "рассудительный и эрудированный человек", а не так давно Жозеф Гиз (Joseph Gies), главный редактор Британской Энциклопедии заявил, что будущие ученые во все времена "будут отдавать свой долг Леонардо Пизанскому, как одному из величайших интеллектуальных первопроходцев мира". Его работы после долгих лет только сейчас переводятся с латинского языка на английский. Для тех, кто интересуется - книга, названная Ленардо Пизанский и новая математика Средних веков Жозефа и Франца Гиз (Joseph and Frances Gies) является прекрасным трактатом по веку Фибоначчи и его работам.

Хотя он и был величайшим математиком средних веков, единственные памятники Фибоначчи - это статуя напротив Пизанской башни через реку Арно и две улицы, которые носят его имя, одна - в Пизе, а другая - во Флоренции. Кажется странным, что так мало посетителей к 179-ти футовой Падающей башне когда-либо слышали о Фибоначчи или видели его статую. Фибоначчи был современником Бонанна (Bonanna), архитектора Пизанской башни, строительство которой тот начал в 1174 году. Оба они сделали вклад в мировую историю, но один, чей вклад намного превосходит другого, почти неизвестен.

Последовательность Фибоначчи

В Книге абака одна из поставленных проблем дает начало последовательности чисел 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и так далее до бесконечности, известной сегодня как последовательность Фибоначчи. А проблема такова:

В поисках решения, мы находим, что каждой паре, включая первую, необходим месяц для достижения зрелости, но, начав воспроизводство, они производят на свет новую пару каждый месяц. Количество пар остается тем же в начале каждого из двух первых месяцев, то есть, последовательность - 1, 1. Эта первая пара, наконец, удваивает свое количество во втором месяце, так что в начале третьего месяца у нас уже две пары. Из них старшая пара производит третью пару, так что в начале четвертого месяца последовательность увеличивается до 1, 1, 2, 3. Из этих трех две старшие пары, но не младшая, воспроизводятся так, что последовательность увеличивается до 1, 1, 2, 3, 5, 8 и так далее. Рис. 3-1 показывает семейное дерево Кроликов, разрастающееся с логарифмической прогрессией. Продолжите последовательность в течение нескольких лет и количество станет астрономическим. Через 100 месяцев, например, мы вынуждены будем бороться с 354 224 848 179 261 915 075 парами кроликов. Последовательность Фибоначчи, проистекающая из кроличьей проблемы, обладает множеством интересных свойств и показывает почти постоянное соотношение среди своих компонентов.

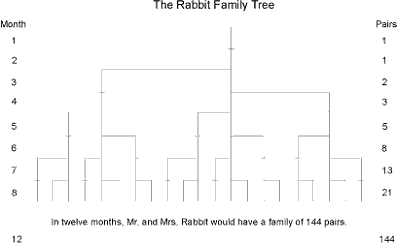
Рисунок 3-1

The Rabbit Family Tree - Семейное дерево Кроликов
Month - Месяц
Pairs - Пары
Подпись - Через 12 месяцев мистер и миссис Кролик имели бы семью из 144 пар.

Сумма любых чисел, расположенных рядом в последовательности, дает следующее число последовательности, а именно 1+1=2, 1+2=3, 2+3=5, 3+5=8 и так далее до бесконечности.

Золотая пропорция

После первых нескольких чисел в последовательности, отношение любого числа к следующему старшему равна примерно 0.618 к 1, а к соседнему младшему - приблизительно 1.618 к 1. Чем дальше вдоль последовательности, тем ближе отношение приближается к фи ( 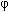*), которое является иррациональным числом 0.618034.. Соотношение между числами, расположенными через одно в последовательности, приблизительно равно 0.382, что является инверсией от 2.618 (1:2.618*). Обратитесь к таблице соотношений всех чисел Фибоначчи от 1 до 144 (рис. 3-2).

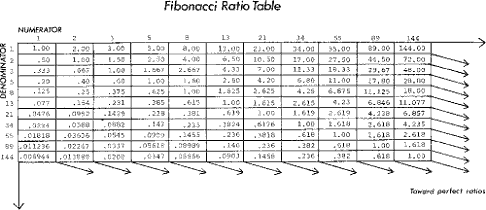
Рисунок 3-2

Фи является единственным числом, которое после сложения с 1 дает свою же инверсию: 0.618+1=1:0.618. Такой альянс аддитивных и мультипликативных свойств порождает следующую последовательность равенств:

0.618² = 1 - 0.618,
0.618³ = 0.618 - 0.618²,
0.618⁴ = 0.618² - 0.618³,
0.618⁵ = 0.618³ - 0.618⁴, и т.д.

или, альтернативно:

1.618² = 1 + 1.618,
1.618³ = 1.618 + 1.618²,
1.618⁴ = 1.618² + 1.618³,
1.618⁵ = 1.618³ + 1.618⁴, и т.д.

Некоторые формулировки из взаимосвязанных свойств этих четырех соотношений могут быть представлены следующим образом:

1) 1.618 - 0.618 = 1,
2) 1.618 * 0.618 = 1,
3) 1 - 0.618 = 0.382,
4) 0.618 * 0.618 = 0.382,
5) 2.618 - 1.618 = 1,
6) 2.618 * 0.382 = 1,
7) 2.618 * 0.618 = 1.618,
8) 1.618 * 1.618 = 2.618.

Кроме 1 и 2, любое число Фибоначчи, умноженное на 4 и добавленное к некоторому выбранному числу Фибоначчи, дает еще одно число Фибоначчи:

3 * 4 = 12; + 1 = 13,
5 * 4 = 20; + 1 = 21,
8 * 4 = 32; + 2 = 34,
13 * 4 = 52; + 3 = 55,
21 * 4 = 84; + 5 = 89, и т.д.

Так как развивается новая последовательность, третья последовательность начинается с тех же чисел, которые добавлялись к произведению на 4. Это соотношение возможно, потому что коэффициент между числами Фибоначчи, отстоящими друг от друга через две позиции равен 4.236, где 0.236 является и инверсией этого коэффициента, и разностью с числом 4. Это непрерывное рядообразующее свойство отражается и в других соотношениях по этим же причинам.

1.618 (или 0.618) известно как Золотая пропорция или Золотое сечение. Его гармония приятна для глаз и является важным явлением в музыке, искусстве, архитектуре и биологии. Вильям Хоффер, написал для декабрьского номера 1975 года журнала Smithsonian Magazine:

Абсурдные кролики Фибоначчи всплывают в самых неожиданных местах. Эти числа, бесспорно, являются частью мистической естественной гармонии, которая приятно осязается, приятно выглядит и даже приятно звучит. Музыка, например, основана на 8-ми нотной октаве. На фортепьяно это представлено 8 белыми клавишами и 5 черными - всего 13. Не случайно, что музыкальная гармония, которая, как кажется, приносит уху величайшее удовольствие, является мажорным шестизвучием. Нота Е (ми*) звучит как соотношение 0.625 к ноте С (до*). Всего лишь на 0.006966 больше точного Золотого сечения, соотношения мажорного шестизвучия вызывают приятные колебания в улитке внутреннего уха - органа, который как раз имеет форму логарифмической спирали.

Непрерывное нахождение чисел Фибоначчи и золотой спирали в природе точно объясняет, почему пропорция 0.618034 к 1 так привлекательна в искусстве. Человек видит изображение жизни в искусстве, которое основано на золотом сечении.

Природа использует Золотое сечение в своих наиболее сокровенных строительных блоках и в наиболее продвинутых образцах, от таких мелких форм, как атомные структуры, микрокапилляры мозга и молекулы ДНК до таких огромных, как планетарные орбиты и галактики. Оно касается таких разнообразных явлений, как расположение квазикристаллов, планетарных расстояний и периодов обращения, отражения световых лучей от стекла, мозг и нервная система, музыкальная аранжировка и строение растений и животных. Наука быстро доказывает, в природе действительно существует основной закон пропорций. Между прочим, вы удерживаете предмет двумя из пяти ваших отростков (две руки, две ноги и голова*), которые имеют три шарнирно соединенных части (плечо, предплечье и кисть*), пять отростков на концах (пальцы*) с тремя шарнирно соединенными частями (фаланги пальцев*). (Авторы намекают на волновую последовательность 5-3-5-3.*)

Геметрия Фибоначчи

Золотое сечение

Любой отрезок может быть разделен таким образом, что соотношение между его меньшей и большей частями будет равно отношению между большей частью и всем отрезком (рис. 3-3). Это отношение всегда равно 0.618.

Рисунок 3-3

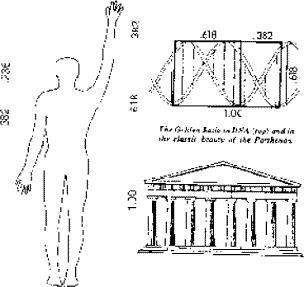
Золотое сечение повсеместно попадается в природе. Действительно, человеческое тело является воплощением Золотых сечений (см. рис. 3-9) во всем от внешних размеров до устройства лица. "Платон, в своих Timaeus (Тимей, натурфилософия*)", - говорит Питер Томпкинс (Peter Tompkins), - "заходит так далеко, что рассматривает фи, а в результате и Золотое сечение, в качестве наибольшего обобщения всех математических соотношений и считает его ключом к физике космоса". В шестнадцатом веке, Иоганн Кеплер (Johannes Kepler), делая заметки о Золотом или "Божественном сечении" сказал, что оно, фактически, характеризует все в мироздании и в частности символизирует сотворение мира Богом "по подобию". Человек делится в поясе на соотношение Фибоначчи. Среднее значение приблизительно равно 0.618. Это соотношение остается справедливым отдельно для мужчин и отдельно женщин, прекрасный знак создания "по подобию". Все ли в развитии человечества также является созданием "по подобию"?

Золотой прямоугольник

Стороны Золотого прямоугольника находятся в пропорции 1.618 к 1. Чтобы построить Золотой прямоугольник, начните с квадрата со сторонами в 2 единицы и проведите линию от середины одной из его сторон к одному из углов у противоположной стороны, как показано на рис. 3-4.

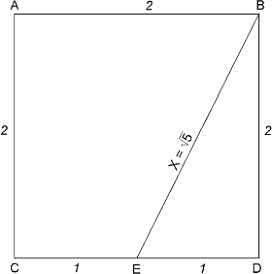
Рисунок 3-4

Треугольник EDB - прямоугольный. Пифагор, около 550 г. до н.э., доказал, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов. В этом случае, следовательно, X2 = 22 + 12, или X2 = 5. Длина гипотенузы ЕВ тогда равна корню квадратному из 5. Следующий шаг в построении Золотого прямоугольника заключается в продолжении линии CD до точки G так, чтобы EG равнялась корню квадратному из 5, или 2.236 единиц длины, как показано на рис. 3-5. После завершения построения, стороны прямоугольника будут соотноситься как Золотая пропорция, поэтому и прямоугольник AFGC, и BFGD являются Золотыми прямоугольниками.

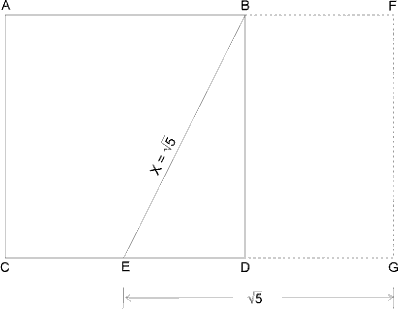
Рисунок 3-5

Так как стороны прямоугольников находятся в соотношении Золотой пропорции, то и сами прямоугольники, по определению, являются Золотыми прямоугольниками.

Произведения в искусстве значительно улучшены с использованием знания Золотого прямоугольника. Притягательность его ценности и употребления были особенно сильны в древнем Египте и Греции и во времена Ренессанса, т.е. во всех важных периодах цивилизации. Леонардо да Винчи (Leonardo da Vinci) придавал огромное значение Золотой пропорции. Он также находил ее приятной в своих соотношениях и говорил: "Если предмет не имеет правильного облика, он не работает". Многие из его картин обладают правильным обликом, потому что он использовал Золотое сечение для того, чтобы усилить их привлекательность.

В то время как пропорция фи использовалась сознательно и продумано художниками и архитекторами по своим собственным причинам, она, очевидно, действительно оказывает влияние на обозревателей таких форм. Экспериментаторы определили, что люди находят соотношение 0.618 эстетически приятным. Например, людей просили выбрать один прямоугольник из группы прямоугольников различных типов, и средний выбор в основном был близок к форме Золотого прямоугольника. Когда просили пересечь одну полоску другой так, как им больше нравится, люди в основном применяли одну полоску для деления другой в соотношении фи. Окна, рамы картин, здания, книги и кладбищенские кресты часто приблизительно соответствуют Золотому прямоугольнику.

Так же, как и Золотое сечение, ценность Золотого прямоугольника едва ли ограничивается красотой, но также служит деятельности. Среди многочисленных примеров, наиболее ярким является тот, что двойная спираль ДНК сама создает Золотое сечение в стандартных интервалах ее изгибов (см. рис. 3-9).

В то время как Золотое сечение и Золотой прямоугольник представляют статические формы естественной и сотворенной человеком красоты и деятельности, представление эстетически привлекательного динамизма, организованного движения роста и развития может быть выполнено только самой прекрасной формой во Вселенной - Золотой спиралью.

Золотая спираль

Золотой прямоугольник можно использовать для построения Золотой спирали. Любой Золотой прямоугольник, как на рис. 3-5, можно разделить на квадрат и меньший Золотой прямоугольник, как показано на рис. 3-6. Этот процесс теоретически можно продолжать до бесконечности. Эти получающиеся прямоугольники, которые мы нарисовали и которые, как оказалось, скручиваются внутрь, промаркированы A, B, C, D, E, F и G.

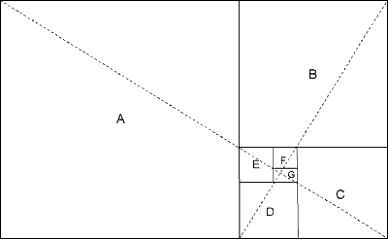
Рисунок 3-6

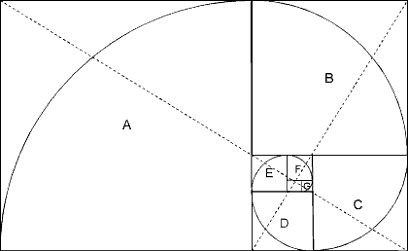
Рисунок 3-7

Пунктирные линии, которые сами находятся в золотом соотношении одна к другой, рассекают прямоугольники по диагонали и точно обозначают теоретический центр скручивающихся квадратов. Приблизительно из центральной точки мы можем начертить спираль, как показано на рис. 3-7, соединяя точки пересечения каждого скручивающегося квадрата в порядке возрастания размера. Так как квадраты скручиваются внутрь и наружу, их точки соединения выписывают Золотую спираль. Для построения Золотой спирали может применяться такой же процесс, но с использованием скручивающихся треугольников.

В любой точке развития Золотой спирали, отношение длины дуги к ее диаметру равно 1.618. Диаметр и радиус в свою очередь соотносятся с диаметром и радиусом, отстоящих на угол в 90 градусов, с коэффициентом 1.618, как показано на рис. 3-8.

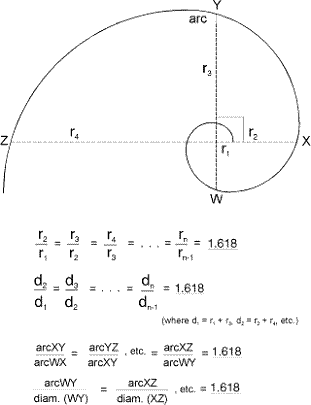
Рисунок 3-8

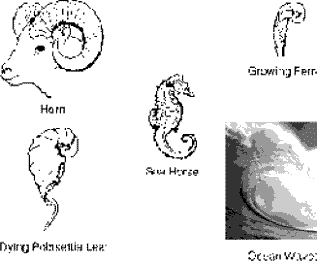
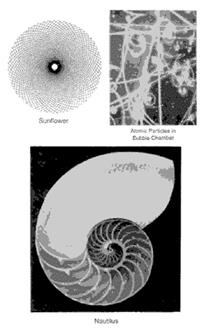
Золотая спираль, которая является разновидностью логарифмической или изогональной спирали, не имеет границ и является постоянной по форме. Из любой точки спирали можно двигаться бесконечно или в направлении внутрь, или наружу. Центральная часть логарифмической спирали, рассмотренная через микроскоп, имела бы тот же облик, что и самая широкая видимая ее часть на удалении многих световых лет. Как указывал Давид Бергамини (David Bergamini) в Математике, хвост кометы раскручивается от солнца в форме логарифмической спирали. Паук Epeira прядет свою паутину в виде логарифмической спирали. Бактерии размножаются в логарифмической прогрессии, которую можно начертить в виде логарифмической спирали. Метеориты, врезаясь в поверхность Земли, формируют впадины, которые соотносятся с логарифмической спиралью. Сосновые шишки, морские коньки, раковины улиток, раковины моллюсков, волны океана, папоротники, рога животных и расположение семян подсолнуха и маргаритки - все они образуют логарифмические спирали.

Облака циклона и галактики открытого космоса скручиваются в логарифмические спирали. Даже человеческий палец, который составлен из трех фаланг, находящихся по отношению друг к другу в Золотой пропорции, принимает спиральную форму умирающего листа, когда сжимается. На рис. 3-9 мы видим отражение этого космического влияния в многочисленных формах. Вечность времени и световые годы космоса разделяют сосновую шишку и спиральную галактику, но строение остается тем же самым: коэффициент 1.618, возможно, первостепенный закон, управляющий активными природными явлениями. Таким образом, Золотая спираль развертывается перед нами в символической форме, как один из величественных замыслов природы, образ жизни в бесконечном расширении и сжатии, статический закон, управляющий динамическим процессом, подкрепленный и изнутри, и снаружи пропорцией 1.618, Золотым сечением.

Рисунок 3-9a	Рисунок 3-9b
Рисунок 3-9c	Рисунок 3-9d
Рисунок 3-9e
Рисунок 3-9f

Значение Фи

Значение этого вездесущего явления было глубоко осмысленно и высоко оценено величайшими умами различных эпох. История изобилует примерами исключительно образованных людей, которые сохраняли особую притягательность к этой математической формуле. Пифагор отдавал предпочтение пятиконечной звезде, в которой каждый сегмент был в золотой пропорции по отношению к следующему меньшему сегменту, как символ его религиозного Ордена; у знаменитого математика 17 века Якоба Бернулли (Jacob Bernoulli) была Золотая спираль, выгравированная в камне; у Исаака Ньютона (Isaac Newton) была такая же спираль, вырезанная на спинке его кровати (принадлежащей сейчас Гравитационному фонду, Нью Бостон). Самыми ранними приверженцами были зодчие Египетских пирамид у города Гиза, которые закодировали знание о фи в своих конструкциях около 5000 лет назад. Египетские конструкторы сознательно внедрили Золотую пропорцию в Великую пирамиду, придав ее фасаду наклонную высоту в 1.618 раз больше половины ее основания так, что вертикальная высота пирамиды в то же самое время являлась корнем квадратным из длины половины основания, умноженной на 1.618.

Согласно заявлению Питера Томпкинса (Peter Tompkins), автора Секретов Великой пирамиды (1971), "Это соотношение показывает, что сообщение Геродота (Herodotus; древнегреческий историк, 5 в. до н.э.*) действительно справедливо в том, что квадрат высоты пирамиды равен 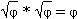, и площадь фасада 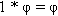". Более того, применяя эти соотношения, Египетские ученые (очевидно, для того, чтобы построить масштабную модель Северного полушария) использовали пи ( 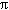) и фи ( 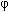) в подходе настолько математически изощренном, что он достигал искусства квадратуры круга и кубатуры сферы (т.е. создавая их равными по площади и объему), мастерство, которое не смогли повторить в течение более четырех тысячелетий.

В то время как простое упоминание Великой пирамиды может служить высеченным из камня побуждением к скептицизму (возможно, по разумной причине), помните, что ее форма отражает ту же самую привлекательность, которую поддерживала западная научная, математическая, художественная и философская мысль, включая Платона, Пифагора, Бернулли, Кеплера, да Винчи и Ньютона. Те, кто сконструировал и построил эту пирамиду, несомненно, были блестящими естествоиспытателями, астрономами, математиками и инженерами. Ясно, что они хотели сохранить в течение тысячелетий Золотую пропорцию, как нечто, обладающее необыкновенной важностью. То, что людей такого масштаба позже увлекли величайшие умы Греции и эпохи Просвещения в их приверженности к этой пропорции, важно само по себе. Что касается причины, то все, что мы имеем, это гипотеза нескольких авторов. Однако эта гипотеза, какой бы непонятной ни была, странно подходит к нашим собственным наблюдениям. Было высказано предположение, что Великая пирамида в течение веков после того, как была построена, использовалась в качестве храма посвящения для тех, кто показал себя достойным понимания великих вселенских секретов. Только те, кто смог возвысится над примитивным восприятием вещей, какими они казались, для того, чтобы открыть то, чем в действительности они были, могли быть посвящены в "тайны", т.е. в систему истин вечного порядка и роста. Входило ли фи в такие "тайны"? Томпкинс объяснял: "Египтяне времен фараонов, утверждает Швалер де Любиц (Schwaller de Lubicz), считали фи не числом, а символом созидательной функции или воспроизводства в бесконечной последовательности. Для них оно символизировало "огонь жизни, мужское семя, логос [на который ссылается] евангелие св. Иоанна"". Логос, греческое слово, было разносторонне определено Гераклитом (Heraclitus) и более поздними языческими, иудейскими и христианскими философами, обозначающим рациональный порядок вселенной, неотъемлемый закон природы, жизнеобразующую силу, сокрытую в вещах, созидательную силу вселенной, управляющей миром и насыщающей его.

Читая это трудное для понимания и еще неясное описание, учтите, что те люди не могли ясно видеть все, что они чувствовали. У них не было графиков и Закона волн, чтобы сделать ясной модель развития природы, и они делали все, что могли, чтобы описать те организационные принципы, формирующие естественный мир, которые они разглядели. Если те древние философы были правы в том, что всемирная созидательная сила управляет и пронизывает вселенную, то почему бы ей не управлять и не насыщать мир человека? Если формы во всей вселенной, включая человеческое тело, мозг и ДНК отражают формы фи, может ли человеческая деятельность отражать ее так же? Если фи является жизненной силой во вселенной, может ли она быть побуждением в основе развития производственной деятельности человека? Если фи является созидательной функцией, может ли оно управлять созидательной деятельностью человека? Если развитие человека основано на производстве и воспроизводстве в "бесконечной последовательности", разве не разумно то, что такой процесс обладает спиральной формой фи и что эта форма различима в движении совокупной оценки его производственного потенциала, т.е. фондового рынка? Так же, как посвященные египтяне изучали скрытые истины построения и роста во вселенной за видимыми случайностями и хаосом (нечто, что, наконец, вновь открыла современная "теория хаоса" в 1980х), так и фондовый рынок, по нашему мнению, может быть должным образом истолкован, если рассматривать его суть, а не то, чем он кажется при поверхностном рассмотрении. Фондовый рынок - это не случайная бесформенная неразбериха, реагирующая на текущие события, но удивительно точная запись строгой структуры развития человечества.

Сравните эту концепцию со словами астронома Вильяма Кингсланда (William Kingsland) в книге Великая пирамида в фактах и теории о том, что египетские астрономия/астрология была "наукой для особо посвященных, связанной с великими периодами человеческой эволюции". Закон волн объясняет великие периоды человеческой эволюции и показывает, как и почему они развиваются именно так. Более того, он охватывает и в микро-, и в макро-масштабе все, что базируется на парадоксальном принципе динамизма и изменения в пределах неизменной формы. Именно эта форма создает структуру и единство вселенной. Ничего в природе не предполагает, что жизнь является чем-то беспорядочным или бесформенным. Слово "вселенная" означает "единый порядок". Если жизнь обладает формой, тогда мы не должны отрицать возможность того, что человеческое развитие, которое является частью реальности жизни, также обладает порядком и формой. Если продолжить, то фондовый рынок, который оценивает производственную предприимчивость человека, также должен обладать порядком и формой. Все технические подходы к постижению рынка зависят от основного закона порядка и формы. Теория Эллиотта, тем не менее, продвигается дальше других. Она гласит, что не важно, насколько маленькой или насколько большой является форма, основная модель остается неизменной.

Эллиотт в своей второй монографии использовал название Закон Природы - секрет Вселенной в предисловии к Закону волн и применил его ко всем видам человеческой деятельности. Возможно, Эллиотт зашел слишком далеко в высказывании, что Закон волн является секретом вселенной, так как природа создала множество форм и процессов, а не только одну простую композицию. Тем не менее, некоторые величайшие ученые прошлого, упомянутые ранее, возможно, согласились бы с формулировкой Эллиотта. Как минимум, следует сказать, что Закон волн является одним из самых важных секретов вселенной. Даже такое претенциозное утверждение поначалу может показаться практически настроенным инвесторам только хвастливой болтовней, вполне понятно почему. Великая природа этой концепции усиливает воображение и приводит в замешательство интеллект, в то время как ее применимость еще не ясна. Сначала мы должны сказать можем ли мы и теоретически предполагать, и воочию наблюдать, что действительно существует закон, который функционирует на той же математической основе на небесах и на земле так же, как и на фондовом рынке?

Ответ - да. Фондовый рынок обладает именно такой же математической основой, как и природные явления. Идеализированная концепция Эллиотта о развитии рынка является превосходной основой, с которой необходимо строить Золотую спираль, как показывает рис. 3-10 в грубом приближении. В этой конструкции вершина каждой последующей волны старшего волнового уровня является точкой соприкосновения с логарифмическим развитием.

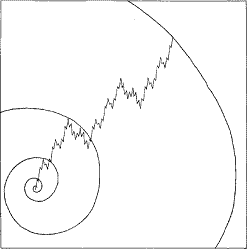
Рисунок 3-10

Такой результат возможен, потому что на каждом уровне деятельности фондового рынка, бычий рынок подразделяется на пять волн, а медвежий рынок - на три волны, давая нам соотношение 5-3, т.е. математическую основу Закона волн Эллиотта. Мы можем воспроизвести полную последовательность Фибоначчи, как мы впервые сделали на рис. 1-4, используя концепцию Эллиотта о развитии рынка. Если мы начнем с простейшего выражения концепции медвежьего движения, мы получим одну прямую нисходящую линию. Бычий взлет в простейшей форме является одной прямой восходящей линией. Полный цикл - две линии. На следующем уровне сложности, соответствующие числа 3, 5 и 8. Как показано на рис. 3-11, эта последовательность может быть продолжена до бесконечности.

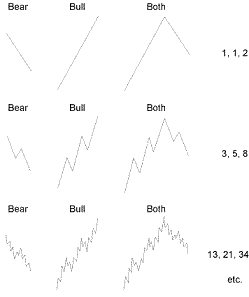
Рисунок 3-11