Тема 19. Одномерные статистики и проверка гипотез

При проведении маркетинговых исследований часто необходимо получить информацию об одной переменной. Например;

· Какое число потребителей хорошо информировано о предлагаемом новом товаре?

· Каково соотношение между разными группами потребителей товара: много использующими, средне, или не использующими товар?

· Какова средняя степень осведомленности о товаре? Сильно ли различается степень осведомленности потребителей о новом товаре?

Такие данные можно получить в результате анкетирования целевой группы и анализировать с помощью частотного анализа. Частотный анализ предполагает подсчет числа ответов респондентов, по каждому из значений переменной, в отношении которой проводится анализ. Подсчет распределения частот значений переменной дает возможность построить таблицу, с указанием общего числа респондентов, отметивших значение переменной, а также преобразование полученных частот в проценты и набегающий итог для всех значений этой переменной.

Частотный анализ помогает определить долю респондентов, оставивших вопрос без ответа, а также указывает долю ошибочных ответов. По каждой категории необходимо показывать не только общее число случаев, но и число допустимых. Число пропущенных ответов и их процент может быть указан в качестве примечания к таблице.

Кроме того, можно установить наличие посторонних значений или выбросов, т.е. случаев с экстремальными значениями. Они не являются ошибками, а скорее наблюдениями, которые настолько сильно отличаются от остальных, что встает вопрос, следует ли их включать в общую статистику, исключать из анализа или искать особые факторы, которые обусловили это экстремальное значение.

Результаты частотного анализа полезно представить в виде распределениярассматриваемойпеременной. Нагляднее всего представить распределение в виде гистограммы, на которой значения переменной размещаются по оси Х, а частота, или относительная частота появления значений указывается по оси У. Также на основе полученной гистограммы можно построить полигон частот, который получается из гистограммы путем соединения верхних точек столбцов прямыми линиями.

Еще один удобный способ представления распределения данных называется кумулятивная функция распределения.При этом подходе определяется число наблюдений со значениями меньше или равными специфицированной величине, т.е. генерируются кумулятивные частоты (набегающим итогом). Кумулятивная функция распределения может использоваться для расчета некоторых широко используемых показателей, таких как медиана, квартили и перцентили.

Для того чтобы обобщить сырые данные таблицы, в которую исследователи сводят результаты всех опросов, используют описательные статистики:

· показатели центра распределения (среднее, мода и медиана),

· показатели вариации (размах, межквартальный размах, стандартное отклонение и коэффициент вариации),

· показатели формы распределения (асимметрия и эксцесс)

Среднее арифметическое или выборочное среднее(mean) – это наиболее часто используемый показатель, характеризующий положение центра распределения. Он используется для оценки среднего значения в случае, если данные собраны с помощью интервальной или относительной шкалы.

Среднее арифметическое X задается формулой:

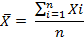
где Xi – значение переменной для i-го респондента, n – общее число ответов.

Мода (mode) – значение переменной, которое чаще всего встречается в выборочном распределении. Представляет наивысшую точку (пик) распределения.

Медиана (median)– значение переменной, которое приходится на середину распределения частот, т.е. одна половина всех значений больше медианы, а другая половина - меньше. Медиана— это 50-й перцентиль. Она характеризует положение центра распределения порядковых данных

Каждый из вышерассмотренных показателей определяет центр распределения по-разному. Если переменную измеряют по номинальной шкале, то лучше использовать моду. Если переменную измеряют по порядковой шкале, то больше подходит медиана. Самый лучший показатель для интервальной или относительной шкалы – среднее арифметическое, а мода и медиана плохо отражают положение центра распределения. Однако среднее арифметическое чувствительно к выбросам значений и если они есть, то лучше использовать два показателя – среднее и медиану.

Показатели вариации (measures of variability), вычисляются на основании данных, измеряемых с помощью интервальных или относительных шкал и включают размах вариации, межквартильный размах, дисперсию, стандартное отклонение и коэффициент вариации.

Размах вариации (range) –это разность между наибольшим и наименьшим значениями переменной в вариационном ряду. На это значение очень сильно влияют выбросы.

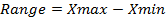
Межквартильный размах (interquartile range) — это разность между 75- и 25-м перцентилями, т.е. размах вариации распределения, охватывающий центральные 50% всех наблюдений.

Разность между средним значением переменной и ее наблюдаемым значением называют отклонением от среднего. Дисперсия(variance) – среднее из квадратов отклонений переменной от ее средней величины. Если значения данных сгруппированы вокруг среднего, то дисперсия невелика. И наоборот, если данные разбросаны, то мы имеем дело с большей дисперсией.

Среднеквадратическое(стандартное) отклонение(standard deviation) равно квадратному корню из дисперсии. Стандартное отклонение выборки Sxвычисляют следующим образом;

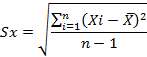
где Xi – значение переменной для i-го респондента, 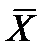– среднее арифметическое ответов по переменной, n – общее число ответов.

Среднеквадратическое (стандартное) отклонение имеет смысл при анализе интервальных и относительных переменных. Этот показатель содержит важную информацию о разбросе и всегда рассчитывается наряду со средним значением. Однако следует принимать во внимание, что на его значение может сильно зависеть от величины выбросов выборки.

Коэффициент вариации(coefficient of variation) — это отношение стандартного отклонения к среднему арифметическому, выраженное в процентах. Коэффициент вариации — показатель относительной изменчивости переменной. Он имеет смысл, только если переменную измеряют по относительной шкале.

Коэффициент вариации CV вычисляют так:

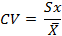
Показатели формы распределения, как и показатели вариации, также полезны для понимания природы распределения переменной. Форму распределения оценивают с помощью асимметрии и эксцесса. При симметричном распределении частоты любых двух значений переменной, которые расположены на одном и том же расстоянии от центра распределения, одинаковы. Равны между собой также и значения среднего арифметического, моды и медианы. Распределение асимметрично(skewness), если значения переменной, равноудаленные от среднего, имеют разную частоту, т.е. одна ветвь распределения вытянута больше другой. Эксцесс(kurtosis) - это показатель относительной крутости кривой частотного ряда по сравнению с нормальным распределением.

Проверка гипотез

Базовый анализ данных неизменно включает в себя статистическую проверку гипотез. Это необходимо потому, что маркетологи почти всегда работают с выборкой, а не с совокупностью, и полученный результат может оказаться справедливым только для этой конкретной выборки, а не для всей генеральной совокупности. Однако благодаря процедуре проверки гипотез можно выработать критерии принятия результатов как достоверных применительно ко всей совокупности.

Существует общая схема проверки гипотезы, которая применима к проверке гипотез, выдвигаемых в ходе маркетинговых исследований.

1) Сформулировать нулевую гипотезу Ho и альтернативную гипотезу Hα после анализа исследуемой проблемы.

2) Выбрать подходящий метод статистической проверки гипотезы, соответствующий поставленной проблеме и задать распределение выборки для проверяемой выборочной статистики.

3) Выбрать уровень значимости а.

4) Определить размер выборки и собрать данные. Вычислить значение выборочной статистики.

5) Определить вероятность проверяемой статистики, выбранной на этапе 2, при условии выполнения нулевой гипотезы, используя соответствующее выборочное распределение. Альтернативный вариант данного этапа: определить критическое значение статистики, которое делит интервал на область принятия и непринятия нулевой гипотезы.

6) Сравнить полученную вероятность с заданным уровнем значимости. Альтернативный вариант данного этапа: определить, попадает ли выборочное значение статистики, построенной по результатам выборочного наблюдения в область принятия или отклонения нулевой гипотезы.

7) На основе выполненного сравнения, отвергнуть или не отвергать нулевую гипотезу и сделать выводы относительно исследуемой маркетинговой проблемы.

На первом этапе маркетолог формулирует нулевую и альтернативную гипотезы.

Нулевая гипотеза Но утверждает, что между определенными статистическими параметрами генеральной совокупности (средними или долями) и полученными результатами выборки не существует связи или различия, т.е. полученные результаты не являются истинными для генеральной совокупности. Исследователи обычно стремятся отвергнуть нулевую гипотезу в пользу альтернативной и проверяют именно нулевую гипотезу.

Альтернативная гипотеза Hα предполагает, что между определенными статистическими параметрами генеральной совокупности (средними или долями) и полученными результатами в ходе опроса или наблюдения есть связь или различия.

Проверка гипотез имеет два исхода: нулевая гипотеза отвергается, а альтернативная – принимается, или нулевая гипотеза не отклоняется, исходя из представленных доказательств. Гипотезы могут быть отвергнуты, или не отвергнуты, но не могут быть приняты как истинные, т.к. дополнительные данные могут доказать их несостоятельность.

В маркетинговых исследованиях нулевую гипотезу формулируют так, что ее непринятие ведет к желаемому заключению. Альтернативная гипотеза представляет собой заключение, для которого маркетологи ищут доказательство справедливости. На языке статистики исследователи совершают ошибку первого рода (α), когда они отвергают верную нулевую гипотезу, и, следовательно, принимают альтернативную; они совершают ошибку второго рода (β), когда они не отвергают ложную нулевую гипотезу, которую должны бы были признать неверной. Для целей проверки нулевая гипотеза предполагается верной. Буквами α и β обозначаются вероятности, ассоциируемые с появлением этих ошибок. Ошибки двух родов не являются дополняющими друг друга (т.е. α+β≠1).

Например, руководство универмага хотело бы начать торговлю своими товарами через Internet. Новую услугу будет выгодно ввести в действие, если свыше 30% пользователей Internet используют сеть для совершения покупок. Маркетолог записывает гипотезы следующим образом:

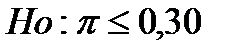
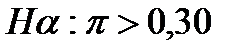
Если нулевую гипотезу Но отклоняют, то принимают альтернативную гипотезу Нα и значит, стоит ввести новую услугу – Internet-магазин. С другой стороны, если нулевую гипотезу Но не отклоняют, то новую услугу не стоит внедрять до тех пор, пока не будет получено дополнительных доказательств для того, что выгодно заниматься Internet-торговлей.

В рассматриваемом случае для проверки гипотезы используют односторонний критерий(one-tailed test), так как альтернативная гипотеза имеет четко выраженное направление: доля пользователей Internet, которые используют его для приобретения товаров, больше 0,30.

Предположим, что исследователь хочет проверить предположение, что доля пользователей Internet, делающих покупки в сети не изменилась по сравнению с прошлым годом и действительно составляет 30%.

Когда альтернативная гипотеза не имеет четкой направленности, используется двусторонний критерий(two-tailed test), а гипотезы записываются в следующем виде:

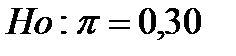
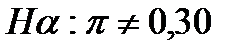
В практике маркетинговых исследований односторонний критерий используют чаще, чем двусторонний. Обычно существует какое-либо предпочтительное направление изменения характеристик, подлежащее доказательству. Например, чем выше прибыль, объем продаж и качество продукта, тем это лучше для фирмы.

Навтором этапеосуществляется выбор подходящего метода проверки. Для проверки нулевой гипотезы необходимо выбрать подходящий статистический метод. Исследователь должен принимать во внимание саму процедуру вычисления выборочной статистики и характерное для нее выборочное распределение. Выборочная статистика (test statistic) служит для того, чтобы можно было сделать вывод о том, насколько близко выборка соответствует нулевой гипотезе. Ее также можно определить как меру соответствий выборки нулевой гипотезе. Предположим, что мы имеем дело с большим объемом выборки и нормальным распределением. Поэтому в нашем примере наиболее приемлема z-проверка. Она вычисляется по формуле:

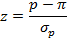
где р – выборочная доляпользователей Internet, совершающих покупки в сети, 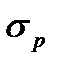–среднеквадратическое отклонение распределения выборочных р. В свою очередь, 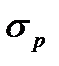равно:

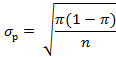
где n – объем выборки

Натретьем этапепроводится выбор уровня значимости или, другими словами, вероятности совершения ошибки первого рода (α). В нашем примере ошибка I рода имела бы место, если мы, исходя из данных выборки, установили бы, что доля потребителей, предпочитающих новый вид услуг, больше 0,30 (30%), в то время как фактически она была бы меньше либо равна 0,30.

Вероятность ошибки первого рода устанавливается, исходя из допустимого уровня риска отклонения истинной нулевой гипотезы, т.е. последствий принятия неправильного управленческого решения.

Ошибку II рода (β) имела бы место, если мы, исходя из данных выборки, установили бы, что доля потребителей, предпочитающих новый вид услуг, меньше или равна 0,30, в то время как фактически она была бы больше 0,30. Хоть ошибки двух родов не являются взаимодополняющими (α+β≠1), величина β связана с α. Чрезвычайно низкое значение α (например, 0,001) приведет к недопустимо высокому значению β. Поэтому необходимо сбалансировать два типа ошибок. В качестве компромисса α часто устанавливают равной 0,05; иногда ей присваивают значение 0,01; другие значения α встречаются редко.

На четвертом этапе осуществляется сборданных. Размер выборки определяют, приняв во внимание желаемые значения вероятностей совершения ошибок I и II рода и других количественных факторов, например финансовых ограничений. Затем собирают необходимые данные и вычисляют значение выборочной статистики. Допустим, что 35% респондентов из 150 пользователей Internet указали, что делают покупки в сети.

Напятом этапеопределяют критическое значение z-статистики, используя таблицы нормального распределения (стандартных значений площадей, очерчиваемых кривой нормального распределения) (см. табл. 1 Приложения). Другими словами, мы вычисляем Р – вероятность получения значения рассчитанного нами z, при использовании одностороннего критерия. Однако, нас интересует величина 1-Р т.к. именно ее мы будем сравнивать с выбранным нами значением α.

На шестом этапе мы сравниваем расчетное 1-Р и заданный уровень значимости α и на основе сравнения определяем, попадает ли выборочное значение статистики, построенной по результатам выборочного наблюдения в область принятия или отклонения нулевой гипотезы.

Если 1-Р > α, то нулевая гипотеза не отвергается и, значит, в нашем примере полученный результат исследования не дает основания делать вывод, что доля потребителей, предпочитающих новый вид услуг, больше 0,30. И наоборот, если 1-Р < α, то нулевая гипотеза отвергается, а альтернативная принимается, и это будет означать, что с вероятностью ошибки 5%, можно утверждать, что более 30% пользователей сети делают покупки в Internet. Таким образом, мы перешли к седьмому этапу и можем трансформировать полученные математические результаты в конкретное решение маркетинговой проблемы и сформулировать выводы.

Проверка гипотез об одной переменной. Существуют многочисленные случаи, когда маркетологам необходимо сопоставить результаты выборочных наблюдений с некоторыми заранее определенными стандартами.

Проверка гипотезы	Параметрические методы проверки (метрические данные)	Одна выборка		· t-критерий · z-критерий
Две выборки	Независимые выборки	· Двухгрупповой t-критерий · z-критерий
Парные выборки	· Парный t-критерий
Непараметрические методы проверки (неметрические данные)	Одна выборка		· Критерий 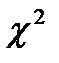· Критерий Колмогорова-Смирнова · Критерий серий · Биномиальный критерий
Две выборки	Независимые выборки	· Критерий 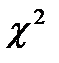· Критерий Манна-Уитни · Критерий Колмогорова-Смирнова · Медианы
Парные выборки	· Критерий знаков · Критерий Вилкоксона · Критерий МакНемара · Критерий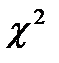

Выделяют много различных вариантов сравнений, и каждый требует проверки гипотезы об одномерном показателе. В зависимости от того, какие данные сравнивают, применяют те или иные методы проверки гипотез. В таблице приведены различные методы проверки гипотез, применяемые в зависимости от того, какие по своей природе данные сравниваются.Метрические данные измеряются по интервальной или относительной шкале, неметрические данные получают на основе номинальной или порядковой шкал.

Выборки считаются независимыми, если выделены случайным образом из различных генеральных совокупностей. Для анализа данные, принадлежащие различным группам респондентов, например мужчинам и женщинам, обычно обрабатывают как независимые выборки. С другой стороны, выборки являются парными (связанными), когда данные двух выборок имеют отношение к одной и той же группе респондентов.

Рассмотрим некоторые методы проверки гипотез, используя конкретные примеры.

1. Проверка согласия по критерию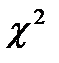

Рассмотрим производителя неких продуктов питания, который разработал новой рецепт продукта, который уже пользуется популярностью у потребителей. На основе данных сканирования по существующим продуктам было установлено, что на одну упаковку, проданную потребителю в возрасте от 18 до 35 лет, приходится три упаковки, проданные покупателю в возрасте от 35 до 55 лет и две упаковки, проданные людям старше 55 лет. Производителю требуется узнать, сохранится ли это соотношение продаж для продукта, изготовленного по новой рецептуре.

Для этого производитель провел рыночный тест для определения относительных частот приобретения нового продукта разными категориями покупателей. В результате надлежащим образом организованного рыночного теста было продано 1200 упаковок нового продукта в течение одной недели. Распределение этого объема продаж выглядит следующим образом: 18-35 лет – 265 упаковок; 35-55 лет – 610 упаковок; старше 55 лет – 325 упаковок.

Полученные цифры не соответствуют образцу соотношения, установленному по традиционной рецептуре продукта. Означает ли это, что продажа нового продукта не будет идти в традиционном соотношении?

Для решения такого типа задач хорошо подходит проверка согласия по критерию 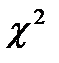.Множество значений, принимаемых интересующей нас переменной разбивается на k взаимоисключающих интервалов (в нашем примере k=3). Каждое наблюдение логически попадает в один из этих интервалов. Фактически это – частотный анализ для переменной «возрастная категория». Предполагается, что испытания (покупки) независимы и объем выборки велик.

Для проведения проверки необходимо определить количество ожидаемых попаданий в рассматриваемые интервалы (ожидаемое число событий) и сравнить их с числом значений из выборки действительно попавших в соответствующие интервалы (наблюдавшимся числом событий), используя уравнение:

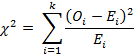
где 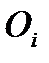- наблюдавшееся число событий, попадающих в i-й интервал; 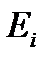- ожидаемое число событий, попадающих в i-й интервал; k – число интервалов.

Ожидаемое число событий получаем из нулевой гипотезы, которая в рассматриваемом примере состоит в том, что распределение продаж нового продукта по возрастным группам будет повторять нормальное для продаж традиционного продукта соотношение 1:3:2. Если бы то продажа 1200 упаковок во время тестирования подчинялась ожидаемому образцу продаж, то потребители в возрасте 18-35 лет приобрели бы 200 упаковок; 35-55 лет – 600 упаковок; старше 55 лет – 400 упаковок. Соответствующая 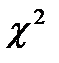статистика рассчитывается следующим образом:

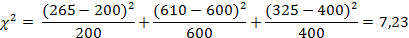
Распределение 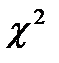полностью определяется величиной, называемой числом степеней свободы n. Под термином «степени свободы» подразумевается такое количество параметров, характеризующих состояние некоторого объекта, которые могут меняться независимо. Как правило, число степеней свободы на единицу меньше числа категорий (n=k - 1), т.е. (n=k - 1=2).

Выберем для этой поверки уровень значимости α=0,05. Табулированное значение 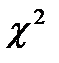для двух степеней свободы и α=0,05 составляет 5,99 (см. Таблицу 1 Приложения). Поскольку рассчитанное значение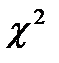 = 7,23 больше, заключение состоит в том, что вероятность случайного получения таких различий (если бы нулевая гипотеза была истинна) меньше 0,05. Таким образом, результаты предварительного рыночного тестирования показывают, что продажи продукта, изготовленного по новой рецептуре, будет идти иным образом, чем считалось типичным для данной продукции. Нулевая гипотеза о продаже в соотношении 1:3:2 отвергается.

Описанная в общих чертах проверка 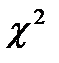является приблизительной. Приближение оказывается сравнительно неплохим, если, как общее правило, ожидаемое число событий в каждой категории равно 5 и более, хотя в некоторых ситуация оно может опускаться даже до 1.