Подсоединенных к одному узлу
Во все ветви электрической цепи, подсоединенные к одному узлу (рис. 2.101), можно включить одинаковые источники напряжения, ЭДС которых равна по величине и направлена к узлу, либо от узла. Подобное включение является эквивалентным, так как в исходной схеме токораспределение остается прежним.

Рисунок 2.101 – Узел электрической цепи
Справедливость такого включения следует из второго закона Кирхгофа, согласно которому, при обходе контура, узел встречается только один раз.
Подобное преобразование рационально проводить для электрических схем, у которых имеются ветви только с одним источником напряжения. Рассмотрим указанное преобразование на примере электрической цепи, изображенной на рисунке 2.102 а.
В первую, вторую и четвертую ветви (рис. 2.102 б) включены источники напряжения по величине равные ЭДС 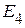 и направлены от узла.
и направлены от узла.

Рисунок 2.102 – Преобразование электрической цепи
Так как в четвертой ветви включены источники напряжения равные по величине и противоположные по направлению, то потенциалы узлов 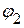 и
и 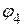 равны. В результате схема имеет вид, представленный на рисунке 2.103.
равны. В результате схема имеет вид, представленный на рисунке 2.103.

Рисунок 2.103 – Преобразованная электрическая цепь
Таким образом, подобное преобразование позволяет уменьшить количество узлов в расчетной схеме.
Пример 2.26.Рассмотрим преобразование электрических цепей, в которых источники напряжения к одному узлу, на примере электрической цепи, приведенной рисунке 2.104, параметры которой Е1 = 20 В, Е2 = 15 В, r3 = 50 Ом, r4 = 150 Ом, r5 = 200 Ом, r6 = 100 Ом.

Рисунок 2.104 –Электрическая цепь постоянного тока
1. Осуществляем предварительный анализ схемы. Количество ветвей – 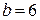 , количество узлов –
, количество узлов – 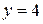 .
.
Первая и вторая ветви содержат только источники напряжения с ЭДС 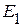 и
и 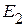 соответственно.
соответственно.
При нахождении токов в ветвях, например, методом непосредственного применения законов Кирхгофа, необходимо составить систему уравнений из шести неизвестных токов. При нахождении токов в ветвях, например, методом контурных токов, необходимо составить систему уравнений из трех неизвестных контурных токов. Нахождение токов в ветвях, методом узловых потенциалов, невозможно, т.к. проводимости первой и второй ветви равны 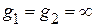 (отсутствуют сопротивления r1 и r2).
(отсутствуют сопротивления r1 и r2).
2. Используя, свойство подключения источников напряжения в ветви, подсоединенные к одному узлу, преобразуем электрическую цепь, приведенную на рисунке 2.104.
В первую, пятую и шестую ветви (рис. 2.105) включены источники напряжения по величине равные ЭДС 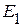 и направлены к узлу. Во вторую, четвертую и шестую ветви (рис. 2.105) включены источники напряжения по величине равные ЭДС
и направлены к узлу. Во вторую, четвертую и шестую ветви (рис. 2.105) включены источники напряжения по величине равные ЭДС 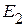 и направлены от узла.
и направлены от узла.

Рисунок 2.105 – Преобразование электрической цепи постоянного тока
Так как в первой и второй ветвях включены источники напряжения равные по величине и противоположные по направлению, то потенциалы узлов 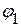 и
и 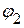 ,
, 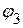 и
и 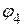 соответственно равны. В результате схема имеет вид, представленный на рисунке 2.106.
соответственно равны. В результате схема имеет вид, представленный на рисунке 2.106.

Рисунок 2.106 – Преобразованная электрическая цепь
Таким образом, количество узлов в расчетной схеме уменьшилось до двух.
3. Рассчитываем токи в преобразованной электрической цепи постоянного тока.
3.1. Осуществляем предварительный анализ схемы.
Количество ветвей – 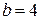 , количество узлов –
, количество узлов – 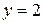 .
.
3.2. Рассчитываем токи в ветвях методом узловых потенциалов.
Потенциал первого узла принимаем равным нулю: 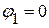 . Следовательно, необходимо определить потенциал
. Следовательно, необходимо определить потенциал 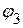 .
.
3.2.1. Составляем уравнение для определения потенциала 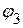 :
:
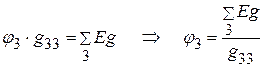 .
.
3.2.1.1. Подставляем числовые значения и находим потенциал 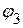 .
.
3.2.1.2. Сумма проводимостей ветвей, подключенных к соответствующим узлам:
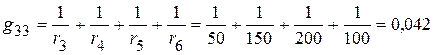 См;
См;
Узловые токи
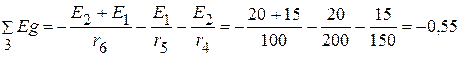 А.
А.
3.2.1.3. После подстановки цифровых значений, определяем потенциал 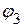 :
: 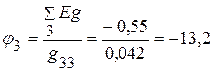 В.
В.
3.3. Определяем токи в ветвях электрической цепи, приведенной на рисунке 2.106.
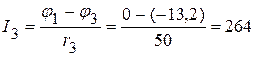 мА,
мА,
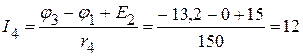 мА,
мА,
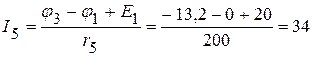 мА,
мА,
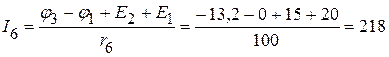 мА.
мА.
3.4. Используя первый закон Кирхгофа, определяем токи 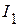 и
и 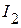 , в электрической цепи, приведенной на рисунке 2.105:
, в электрической цепи, приведенной на рисунке 2.105:
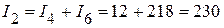 мА;
мА;
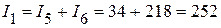 мА.
мА.
4. Проверяем решение, составив баланс мощностей.
4.1. Мощность, генерируемая источниками питания:
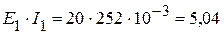 Вт,
Вт,
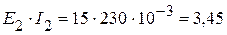 Вт.
Вт.
Суммарная мощность источников:
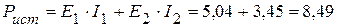 Вт.
Вт.
4.2. Мощность, потребляемая приемниками:
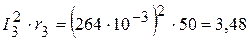 Вт,
Вт,
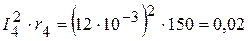 Вт,
Вт,
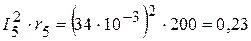 Вт,
Вт,
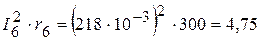 Вт.
Вт.
Суммарная мощность, потребляемая приемниками:
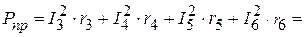
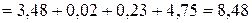 Вт.
Вт.
4.3. Из сравнения генерируемой мощности источником и потребляемой мощности приемниками, следует, что погрешность вычислении 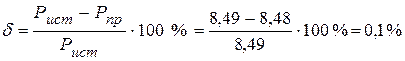 и не превышает 0,5%.
и не превышает 0,5%.
2.5.5. Замена параллельных ветвей эквивалентной ветвью
Допустим, имеется схема, представленная на рисунке 2.107.

Рисунок 2.107 – Схема электрической цепи
Доказательство:
На первом этапе ветви с источниками напряжения и последовательно соединенными резистивными сопротивлениями, заменим эквивалентными ветвями с источниками тока (рис. 2.108).

Рисунок 2.108 – Доказательство замены параллельных ветвей
В результате получим схему с параллельно соединенными источниками тока и ветви с параллельно соединенными сопротивлениями. Ветви с параллельно соединенными источниками тока заменяем эквивалентной схемой:
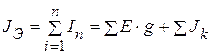 .
.
Ветви с параллельно соединенными сопротивлениями заменяем эквивалентной схемой:
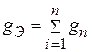 .
.
Подобное доказательство можно обосновать с помощью метода узловых потенциалов. Принимаем потенциал точки 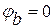 . Тогда
. Тогда
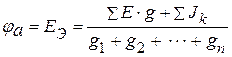 ,
, 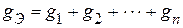 .
.
Дата добавления: 2016-08-23; просмотров: 2216;











