Метод узловых потенциалов
Метод узловых потенциалов для электрических
Схем общего вида
Идея метода узловых потенциалов (МУП). Один из узлов схемы заземляется и его потенциал принимается равным нулю. Далее определяются потенциалы остальных узлов, что дает возможность определить напряжения на зажимах каждой ветви. Затем, используя закон Ома (рис. 2.26), определяем токи в ветвях.
Запишем выражения закона Ома для различных участков цепи, приведенных на рисунке 2.26.

Рисунок 2.26. – Закон Ома: а) с источником напряжения;
б) без источника напряжения
Для участка цепи, содержащего источник напряжения:
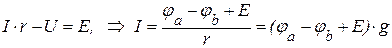 .
.
Для участка цепи, не содержащего источник напряжения:
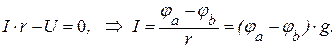
Таким образом, для определения тока к ветвях, необходимо определить потенциалы узлов (напряжения на зажимах ветвей).
Выведем систему уравнений для определения потенциалов узлов произвольной схемы. Для этого используем закон Ома и первый закон Кирхгофа.
Допустим, имеется схема, приведенная на рисунке 2.27.
Заземлим 3 узел, тогда потенциал φ3 = 0.
Потенциалы остальных узлов будут соответственно φ1 и φ2.

Рисунок 2.27 – Электрическая цепь
Используя закон Ома, запишем уравнения для токов в каждой ветви.
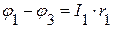 =>
=> 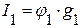 ,
,
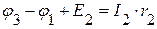 =>
=> 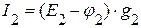 ,
,
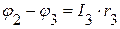 =>
=> 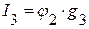 ,
,
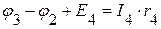 =>
=> 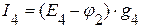 ,
,
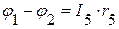 =>
=> 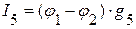 ,
,
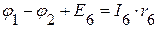 =>
=> 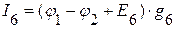 .
.
Уравнения по первому закону Кирхгофа для первого и второго узлов имеют вид:
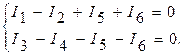
В полученную систему уравнений подставим уравнения для токов, составленных по закону Ома. В результате получим:
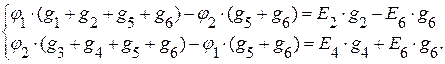
Имеем два уравнения с двумя неизвестными потенциалами φ1 и φ2.
Рассмотрим свойства полученных уравнений.
При составлении первого уравнения потенциал φ1 умножается на сумму проводимостей ветвей, подсоединённых к этому узлу. Влияние потенциала второго узла осуществляется путем введения элемента 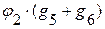 . Этот элемент берется всегда со знаком ”-”. Слагаемое
. Этот элемент берется всегда со знаком ”-”. Слагаемое 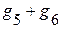 является арифметической суммой проводимостей ветвей, соединяющих 1 и 2 узел.
является арифметической суммой проводимостей ветвей, соединяющих 1 и 2 узел.
В правой части уравнения записывается алгебраическая сумма токов источников питания ветвей, подсоединенных к данному узлу. Если ЭДС источника направлена к узлу, то произведение 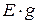 берется со знаком ”+”, если от узла – со знаком ”-“.
берется со знаком ”+”, если от узла – со знаком ”-“.
Используя вышеуказанные свойства запишем систему уравнений для определения потенциалов произвольной схемы.
Допустим, имеется электрическая схема, содержащая n + 1 узлов. Заземляем один узел и имеем n неизвестных потенциалов (соответственно n уравнений).

где 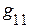 ,
, 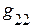 ,
, 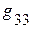 , … ,
, … , 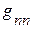 – соответственно сумма проводимостей ветвей, подсоединённых соответственно к 1, 2 … n – ному узлу (всегда со знаком +).
– соответственно сумма проводимостей ветвей, подсоединённых соответственно к 1, 2 … n – ному узлу (всегда со знаком +).
где 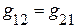 и
и 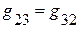 – сумма проводимостей ветвей, соединяющих непосредственно 1 и 2 узел и т.д.
– сумма проводимостей ветвей, соединяющих непосредственно 1 и 2 узел и т.д.
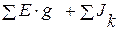 – сумма токов источников питания.
– сумма токов источников питания.
Пример 2.10.Рассмотрим рекомендованный порядок решения МУП на конкретном примере электрической цепи, приведенной на рисунке 2.28, с параметрами E3 = 30 (B), Е2 = 20 В, Е5 = 50 В, r1 = 20 Ом, r2 = 10 Ом, r3= 8 Ом, r4 = 10 Ом, r5 = 10 Ом, r6 = 5 Ом, Jk = 3 А.
1. Осуществляем предварительный анализ схемы. Количество ветвей – 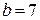 , количество узлов –
, количество узлов – 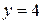 .
.
Потенциал третьего узла принимаем равным нулю: 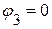 . Следовательно, необходимо определить потенциалы
. Следовательно, необходимо определить потенциалы 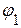 ,
, 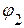 ,
, 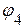 .
.
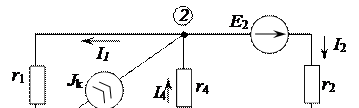
Рисунок 2.28 – Электрическая цепь постоянного тока
2. Составляем уравнения для определения потенциалов 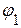 ,
, 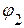 ,
, 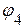 :
:
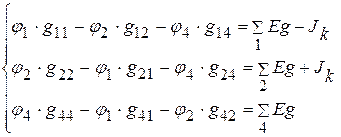
3. Подставляем числовые значения и решаем систему уравнений.
3.1. Проводимости ветвей
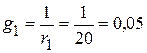 См;
См;
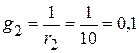 См;
См;
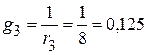 См;
См;
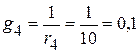 См;
См;
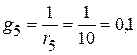 См;
См;
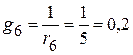 См.
См.
3.2. Сумма проводимостей ветвей, подключенных к соответствующим узлам:
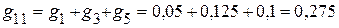 См;
См;
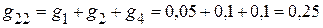 См;
См;
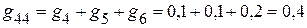 См.
См.
Сумма проводимостей, соединяющих различные узлы
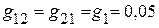 См;
См;
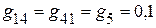 См;
См;
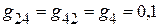 См.
См.
Узловые токи 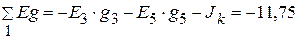 А,
А,
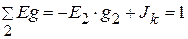 А,
А,
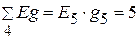 А.
А.
3.2. После подстановки цифровых данных система имеет вид
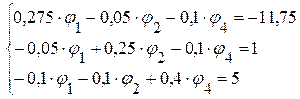
3.3. Решая данную систему уравнений произвольным методом, определяем потенциалы:
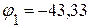 В,
В,
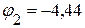 В,
В,
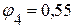 В.
В.
3.4. Определяем токи в ветвях электрической цепи, приведенной на рисунке 2.28.
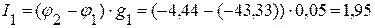 А,
А,
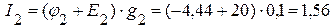 А,
А,
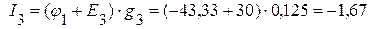 А,
А,
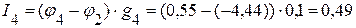 А,
А,
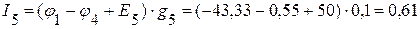 А,
А,
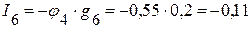 А.
А.
4. Определяем напряжение на зажимах источника тока. Из контура 121:
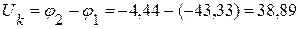 В.
В.
5. Проверяем решение системы уравнений, составив баланс мощностей.
5.1. Мощность источников:
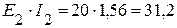 Вт,
Вт,
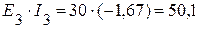 Вт,
Вт,
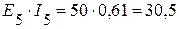 Вт,
Вт,
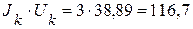 Вт.
Вт.
Знак ”-” указывает на то, что третий источник работает в режиме потребителя электроэнергии (например, зарядка аккумулятора).
Суммарная мощность источников:
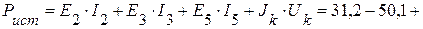
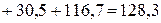 Вт.
Вт.
4.2. Мощность приемников:
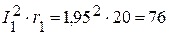 Вт,
Вт,
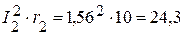 Вт,
Вт,
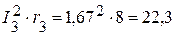 Вт,
Вт,
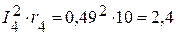 Вт,
Вт,
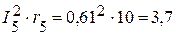 Вт,
Вт,
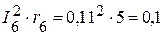 Вт.
Вт.
Суммарная мощность приемников:
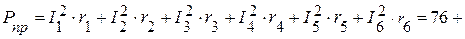
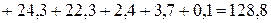 Вт.
Вт.
4.3. Из сравнения генерируемой мощности источниками и потребляемой мощности приемниками, следует, что погрешность вычислении 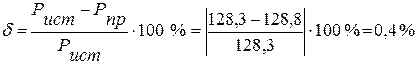 и не превышает 0,5%.
и не превышает 0,5%.
Пример 2.11.Рассмотрим решение задачи, приведенной в примере 2.2, методом узловых потенциалов. Электрическая цепь для рассматриваемого метода, приведена на рисунке 2.29.

Рисунок 2.29 – Электрическая цепь постоянного тока
1. Осуществляем предварительный анализ схемы. Количество ветвей – 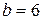 , количество узлов –
, количество узлов – 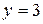 .
.
Потенциал третьего узла принимаем равным нулю: 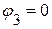 . Следовательно, необходимо определить потенциалы
. Следовательно, необходимо определить потенциалы 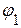 ,
, 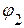 .
.
2. Составляем уравнения для определения потенциалов 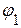 ,
, 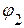 :
:
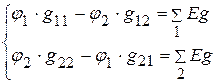
3. Подставляем числовые значения и решаем систему уравнений.
3.1. Проводимости ветвей
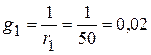 См;
См;
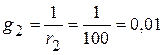 См;
См;
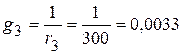 См;
См;
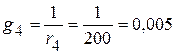 См;
См;
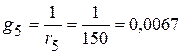 См.
См.
3.2. Сумма проводимостей ветвей, подключенных к соответствующим узлам:
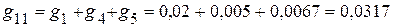 См;
См;
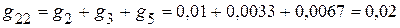 См.
См.
Сумма проводимостей, соединяющих различные узлы
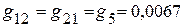 См.
См.
Узловые токи 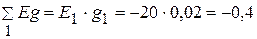 А,
А,
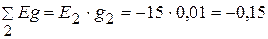 А.
А.
3.2. После подстановки цифровых данных система имеет вид
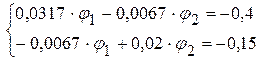
3.3. Решая данную систему уравнений произвольным методом, определяем потенциалы:
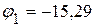 В,
В,
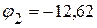 В.
В.
3.4. Определяем токи в ветвях электрической цепи, приведенной на рисунке 2.29.
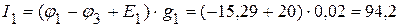 мА,
мА,
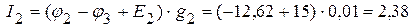 мА,
мА,
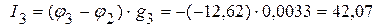 мА,
мА,
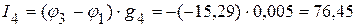 мА,
мА,
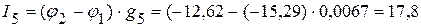 мА.
мА.
Токи в ветвях, рассчитанные в примерах 2.2 и 2.11, совпадают.
Дата добавления: 2016-08-23; просмотров: 2782;











