Основное уравнение неравномерного движения
 При рассмотрении движения воды в открытых руслах в условиях неравномерного режима основная задача состоит в получении зависимости между глубиной потока в данном сечении h и расстоянием l от какого – либо начального сечения (у плотины, у перепада и т.д.) до рассматриваемого сечения.
При рассмотрении движения воды в открытых руслах в условиях неравномерного режима основная задача состоит в получении зависимости между глубиной потока в данном сечении h и расстоянием l от какого – либо начального сечения (у плотины, у перепада и т.д.) до рассматриваемого сечения.
Рассмотрим поток в призматическом русле с прямым уклоном дна
(i > 0), при этом образовалась кривая подпора (рис. 16.8). Выделим в потоке два сечения 1–1 и 2–2, расположенные на малом расстоянии Δl друг от друга. Нормальная глубина потока h0, h – переменная глубина неравно-
Рис. 16.8 мерного движения, Δh – разность между глубинами потока в первом и во втором сечениях. Общее уравнение неравномерного плавноизменяющегося движения в открытом призматическом русле с прямым уклоном дна (i > 0) имеет вид (рассматриваются два бесконечно близкие сечения)
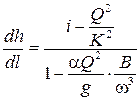 . (16.1)
. (16.1)
16.3. Анализ уравнения неравномерного движения при i > 0
Рассматривая уравнение (16.1)
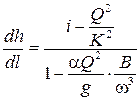 ,
,
видим, что если числитель правой части этого уравнения будет равен
нулю, т.е.
 ,
,
то и левая часть равна нулю и поэтому 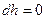 . При этом глубины по длине потока не меняются и уклон свободной поверхности равен уклону дна; в этом случае выражение
. При этом глубины по длине потока не меняются и уклон свободной поверхности равен уклону дна; в этом случае выражение
 или
или 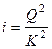
является уравнением равномерного движения 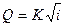 .
.
Далее, очевидно, что знаменатель в правой части может быть положительным, отрицательным и равным нулю; если он равен нулю, т.е.
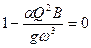 ,
,
то получим
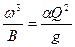 ,
,
что является основным уравнением для определения критической глубины.
В этом случае и левая и правая части уравнения (16.1) обращаются в бесконечность, неравномерное движение перестает быть плавноизменяющимся и образуется гидравлический прыжок (при переходе от глубины меньше критической к глубине больше критической).
Дата добавления: 2016-08-23; просмотров: 3180;











