Основное уравнение гидростатики

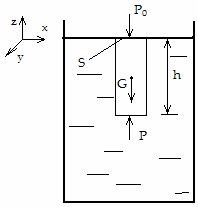Для установления зависимости гидростатического давления от глубины погружения рассмотрим в покоящейся жидкости вертикальный цилиндр (рис. 7.2) высотой h, являющийся частью всего объема и состоящий из жидкости, верх которого совпадает со свободной поверхностью жидкости, а горизонтальная площадь оснований равна S. Цилиндр вместе со всей жидкостью находится в покое, поэтому результирующая F всех сил, действующих на него, равна нулю; следовательно, и проекции этой силы на любую ось равны нулю, в частности

F_x = F_y = F_z= 0.

Массовая сила действует только по оси z, а поверхностные силы давления действуют Рис.7.2 на боковую поверхность; они в силу симметрии равны по величине, противоположны по направлению и вклада в составляющую F_z не вносят. На верхнее основание цилиндра действует давление, которое существует на свободной поверхности, равное 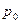, на нижнее основание цилиндра по нормали к нему действует гидростатическое давление 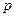. Кроме того, и это очень важно, на выделенный объем (цилиндр) действует сила тяжести (вес) G = ρghS , приложенная в его центре тяжести. Так как имеет место равновесие и F_z=0, то проектируя все силы, действующие на цилиндр на вертикальную ось, получаем

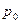S+ ρghS-pS=0. (7.4)

При этом горизонтальные поверхностные силы, действующие только на боковую поверхность, на ось z дадут нулевые проекции. Сократив все члены уравнения (7.4) на S, получим

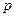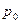= +ρgh. (7.5)

Уравнение (7.5) представляет собой основное уравнение гидростатики, его нужно понимать так: полное давление p в любой точке покоящейся жидкости складывается из давления на ее свободной поверхности 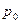и давления ρgh , созданного за счет столба жидкости высотой h.

Пример 7.1.Определить избыточное давление на глубине 4 м. Примем плотность воды ρ=1000 кг/м³ . Тогда по формуле (7.5) имеем

p_изб= ρgh=1000 кг/м^{3 .} 9,8 м/с^{2 .} 4 м=39200 Па=39,2 кПа. Давление 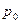на поверхности не учитываем.

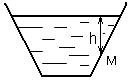Задача 7.1.В сосуд налита вода. Определить давление, которое испытывает стенка сосуда в точке М, находящейся на глубине h=0,5 м.

Решение. Давление на стенку в точке М со стороны жидкости равно .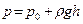

Давление, приложенное к стенке снаружи, равно барометрическому и поэтому результирующее давление 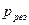, которое будет испытывать стенка, найдется по формуле

p_рез=p₀+ρgh-p_а=ρgh= 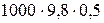=4900 Па (в данном случае p₀= p_а , т.е давление на поверхности жидкости равно атмосферному).

Виды давления

Различают следующие виды давления: барометрическое, абсолютное, избыточное, вакуум.

Барометрическое (атмосферное) давление зависит от высоты места над уровнем моря и от состояния погоды. За нормальное барометрическое давление принимают 760 мм.рт.ст. На свободную поверхность водных потоков, а также естественных и искусственных водоемов действует барометрическое давление.

Абсолютным(полным) давлением р называется давление, определяемое по формуле

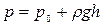, (7.6)

где 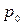- давление на свободной поверхности. Если на свободной поверхности давление равно атмосферному, то разность

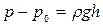(7.7)

называется избыточным давлением (избыточным по сравнению с атмосферным) и обозначается

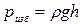. (7.8)

Из последней зависимости следует, что избыточное давление изменяется с глубиной по линейному закону; оно иногда называется манометрическим.

Если давление в точках какого-либо объема жидкости или в закрытых сосудах на свободной поверхности меньше атмосферного (p< p_ат ), то говорят, что в рассматриваемом пространстве вакуум.

Вакуумом называется разность между атмосферным давлением и давлением в разреженном пространстве; иначе говоря, вакуум есть недостаток величины данного давления до атмосферного.

Обозначая величину вакуума через p_в , а давление в разреженном пространстве через p_разр , получим

p_в = p_ат - p_раз (7.9)

Задача 7.2. На какой глубине водолаз будет испытывать избыточное давление 1 ат.? Плотность воды ρ=1000 кг/м³.

Решение. Из решения задачи 5.1 следует, что давление в 1 ат. эквивалентно 98 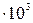Па. Тогда, приравнивая выражение для избыточного давления одной атмосфере, выраженной в паскалях, получим

,

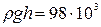откуда

h = 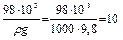м.

Из полученного решения следует, что 10 м водного столба создают избыточное давление в одну атмосферу.

Закон Паскаля

Из уравнения (7.5)

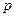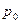= +ρgh

следует, что при изменении давления на поверхности на величину Δp₀ давление во всех точках данного объема изменится на то же значение Δp₀ . Таким образом, жидкость обладает свойством передавать давление. Это свойство выражает закон Паскаля, который формулируется так: всякое изменение давления в какой-либо точке покоящейся жидкости, не нарушающее ее равновесия, передается в остальные ее точки без изменения. На использовании закона Паскаля основано устройство многих гидравлических машин.