Изменение скорости вдоль потока
Средняя скорость потока определяется так
V = 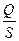 , (6.5)
, (6.5)
и при условии Q = const (нет присоединений и ответвлений) скорость тем больше, чем площадь сечения меньше(знаменатель дроби в (6.5) меньше, а сама дробь больше).
Из (6.5) следует, что расход Q в данном сечении может быть представлен в виде произведения
Q = V·S, (6.6)
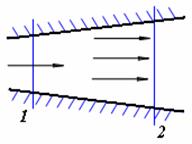
тогда, выбирая два различных по площади сечения трубы, рис.6.8, получим
Q1 = Q2
или
V1S1 = V2S2. (6.7)
Последнее уравнение может быть распространено на любое количество сечений одного и того же потока, например, на n разных сечений
V1S1 = V2S2 = … = VnSn. (6.8)
Равенство (6.7), основываясь на свойстве пропорции, возможно представить так
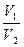 =
= 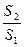 . (6.9)
. (6.9)
 Из него следует, что отношение средних скоростей обратно пропорционально отношению площадей. Для круглой трубы площадь сечения S = πd2/4 и поэтому скорости в сечениях относятся обратно пропорционально квадратам диаметров.
Из него следует, что отношение средних скоростей обратно пропорционально отношению площадей. Для круглой трубы площадь сечения S = πd2/4 и поэтому скорости в сечениях относятся обратно пропорционально квадратам диаметров.
Примеры: 1. Если диаметр трубы увеличить в 2 раза, то средняя скорость в этом сечении уменьшится в 4 раза;
2. Если диаметр трубы в данном сечении уменьшить
в 3 раза, то средняя скорость в этом сечении увеличится
в 9 раз.
Задача 6.2. Скорость в сечении 1 (рис. 6.8) равна 0,8 м/с, диаметр трубы в сечении 1 равен d1 = 50 мм, а Рис.6.8 сечении 2 d2 = 100 мм. Определить скорость в сечении 2.
Решение. Из условия задачи имеем:
S1 = 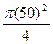 , S2 =
, S2 = 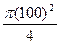 .
.
Учитывая (6.9), получаем значение скорости V2
V2 = V1· 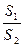 =
= 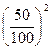 · V1 =
· V1 = 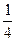 · 0,8 = 0,2 м/с.
· 0,8 = 0,2 м/с.
Дата добавления: 2016-08-23; просмотров: 1780;











