Основные физические свойства жидкостей
Плотность.Плотность 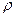 характеризует распределение массы m жидкости по объему W.
характеризует распределение массы m жидкости по объему W.
Плотностью однородной жидкости 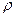 называется отношение массы жидкости к ее объему
называется отношение массы жидкости к ее объему
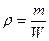 . (5.1)
. (5.1)
В общем случае плотность зависит от давления и температуры, но так как в обычных условиях жидкость находится под атмосферным давлением и изменение температуры незначительно, то плотности жидкостей могут считаться практически постоянными, т.е.
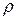 = const.
= const.
Ниже приведены значения плотностей некоторых жидкостей и газов: плотность дистиллированной воды при 4ºС равна 1000 кг/м3, плотность морской воды 1020-1030 кг/м3, нефти и нефтепродуктов – 650-900 кг/м3, ртути – 13596 кг/м3. Плотности газов (при 0ºС и нормальном давлении): воздух – 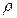 = 1,293 кг/м3, водород –
= 1,293 кг/м3, водород – 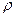 = 0,0898 кг/м3, метан –
= 0,0898 кг/м3, метан –
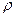 = 0,72 кг/м3.
= 0,72 кг/м3.
Сжимаемость. Сжимаемостью жидкости называется ее свойство уменьшать свой объем под влиянием внешних сил. Жидкости характеризуются очень малой сжимаемостью, например, для пресной воды при температуре от 0 до 20°С и повышении давления на 25 ат. объем жидкости уменьшается на 1/21000 часть своей первоначальной величины. Следовательно, жидкость представляет собой физическое тело, не имеющее определённой формы, но обладающее неизменным объёмом, поэтому при решении большинства гидравлических задач сжимаемость жидкости не учитывается.
Температурное расширение.Жидкости,так же как твердые тела и газы, при изменении температуры изменяют свой объем и плотность. Вода наибольшей плотностью обладает при температуре t = 4ºC: 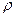 = 1000 кг/м3. При охлаждении воды от 4 до 0ºС объем ее увеличивается и плотность принимает значение
= 1000 кг/м3. При охлаждении воды от 4 до 0ºС объем ее увеличивается и плотность принимает значение 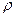 = 999,87 кг/м3. Образующийся из воды лед при температуре 0ºС имеет плотность
= 999,87 кг/м3. Образующийся из воды лед при температуре 0ºС имеет плотность 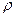 = 918 кг/м3. При нагревании воды выше 4°С объем ее также увеличивается. Свойство жидкости изменять свой объем при изменении температуры оценивается коэффициентом температурного расширения βt. Предположим, что первоначальный объем W при нагревании его от температуры t1 до t2 увеличился на величину ∆W; коэффициент βt определяется так
= 918 кг/м3. При нагревании воды выше 4°С объем ее также увеличивается. Свойство жидкости изменять свой объем при изменении температуры оценивается коэффициентом температурного расширения βt. Предположим, что первоначальный объем W при нагревании его от температуры t1 до t2 увеличился на величину ∆W; коэффициент βt определяется так
βt = 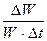 , (5.2)
, (5.2)
где ∆t = t2 – t1.
Величина βt является малой, но не постоянной, а изменяющейся вместе с температурой. Так, например, при атмосферном давлении и изменении температуры от 4 до 10ºС среднее значение 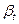 = 0,00004 1/С°.
= 0,00004 1/С°.
Пример 5.1. В системах водяного отопления устраивают расширительные резервуары, присоединяемые к системе в её верхней точке; они устраиваются для аккумулирования прироста объёма воды в системе при её нагревании. Определить наименьший объём расширительного резервуара при колебании температуры воды на 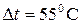 . объём воды в системе W=1,2 м3, коэффициент температурного расширения
. объём воды в системе W=1,2 м3, коэффициент температурного расширения 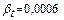 л/град. Изменение объёма воды найдём по формуле (5.2)
л/град. Изменение объёма воды найдём по формуле (5.2)
|
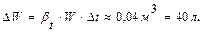
Вязкость. Все жидкости и газы, существующие в природе, обладают вязкостью, которая проявляется в виде трения при
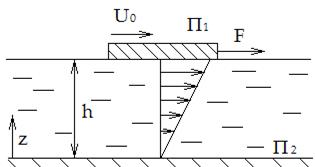
| относительном перемещении | Рис. 5.1 |
частиц. Наряду с легкоподвижными жидкостями (вода, воздух) существуют очень вязкие (глицерин, тяжёлые масла); таким образом, вязкость характеризует степень текучести жидкости. Легко представить поочерёдное перемешивание двух разных жидкостей – например, воды и масла; пока предмет, которым производится перемешивание, неподвижен, вязкость никак не проявляется. Таким образом, сила сопротивления различна в разных жидкостях и возникает только при относительном перемещении частиц. Представим, что на поверхности жидкости глубиной h движется со скоростью 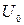 пластина П
пластина П  площадью S, (рис.5.1). Для преодоления силы сопротивления к ней должна быть приложена некоторая сила F. Существование сил трения внутри жидкости приводит к тому, что слой, непосредственно прилегающий к пластине П
площадью S, (рис.5.1). Для преодоления силы сопротивления к ней должна быть приложена некоторая сила F. Существование сил трения внутри жидкости приводит к тому, что слой, непосредственно прилегающий к пластине П  («прилипает» к ней), действует на соседний с ним внутренний слой, этот слой – на следующий и т.д. Как показывают опыты, сила F прямо пропорциональна скорости верхней пластины
(«прилипает» к ней), действует на соседний с ним внутренний слой, этот слой – на следующий и т.д. Как показывают опыты, сила F прямо пропорциональна скорости верхней пластины 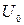 , её площади и обратно пропорциональна расстоянию между пластинами h. Кроме того, эта сила зависит от свойств жидкости – от её вязкости. Например, для глицерина эта сила при прочих равных условиях больше, чем для воды. Сила, действующая на пластину П
, её площади и обратно пропорциональна расстоянию между пластинами h. Кроме того, эта сила зависит от свойств жидкости – от её вязкости. Например, для глицерина эта сила при прочих равных условиях больше, чем для воды. Сила, действующая на пластину П 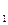 , запишется так
, запишется так
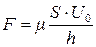 ,
,
где S – площадь пластины, h – расстояние между пластинами; μ – коэффициент вязкости данной жидкости. Если в промежутке между этими пластинами представить два слоя жидкости, то сила их взаимодействия (внутреннего трения в жидкости) равна
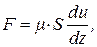 (5.3)
(5.3)
Дата добавления: 2016-08-23; просмотров: 2261;











