Общий случай движения тела (для скоростей).

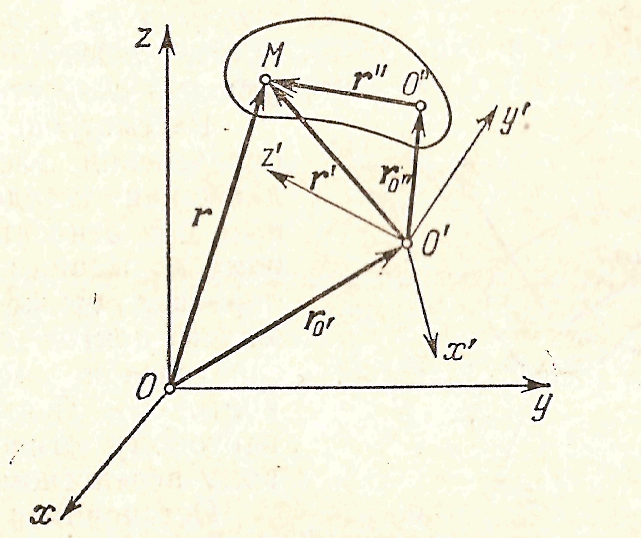
" Рис 50

Рассмотрим следующую задачу в общей постановке. Твердое тело совершает произвольное движение по отношению к системе координат O'x'y'z' (рис 50), которая в свою очередь произвольным образом движется по отно­шению к неподвижной системе координат Охуz. Требуется определить абсо­лютное движение твердого тела, т.е. движение по отношению к системе ко­ординат Охуz. Движение тела по отношению к системе O'x'y'z' определим относитель­ной скоростью 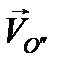его полюса О" и вектором относительной угловой ско­рости 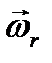вращения вокруг мгновенной оси, проходящей через полюс ОПереносное движение, т. е. движение системы O'x'y'z' по отношению к Охуz , зададим абсолютной скоростью 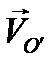полюса О' и вектором угловой скорости 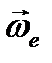вращения вокруг мгновенной оси, проходящей через О'. Определению под­лежат абсолютная скорость 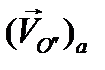полюса О" и абсолютная угловая ско­рость тела 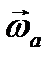. Для произвольной точки М тела, положение которой можно определить в самом теле вектор-радиусом 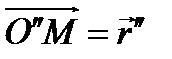, в относительной системе - вектор-радиусом 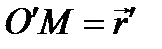и, наконец, в абсолютной системе - вектор-радиусом 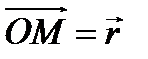, по теореме сложения скоростей имеем

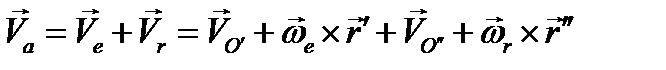(2.44)

причем два первых слагаемых дают в сумме переносную скорость 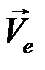точки М, а два последних - ее относительную скорость 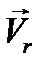. Замечая, что (рис. 50) 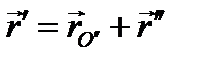будем иметь

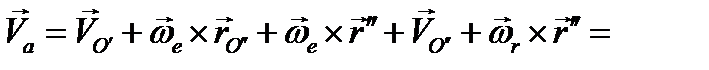
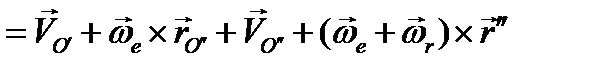Первые два слагаемых представляют собой переносную скорость полю­са О": 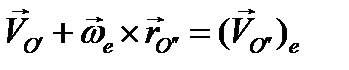, которая в сумме с относительной скоростью 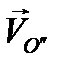того же полюса даст абсо­лютную скорость этого полюса:

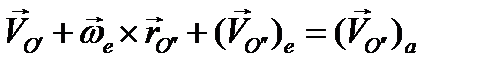
Подстановка в (2.44) дает

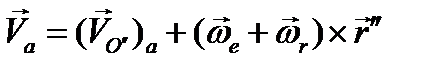
С другой стороны, согласно определению абсолютного движения ско­рость точки М может быть представлена так

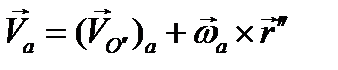
Итак, приходим к следующей тереме сложения движений твёрдого тела: распределение скоростей в абсолютном движении твёрдого тела определяется заданием абсолютной скорости полюса тела, равной геометрической сумме переносной и относительной скоростей полюса, и абсолютной угловой скорости тела, равной геометрической сумме переносной и относительной угловых скоростей тела.