Основные положения теории выравнивания групповых графиков нагрузки
Как известно, основным показателем неравномерности графика нагрузки является его дисперсия, которая равна разности квадратов эффективного и среднего его значений:
DI = Iэ2 - Ic2. (13.5)
Потери электроэнергии DW в 3-фазной сети с сопротивлением R за время Т равны
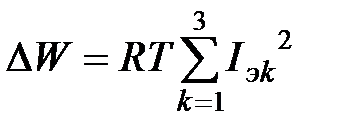 ,
,
где Iэк – эффективный ток k-й фазы, равный, в соответствии с формулой (13.4),
Iэk2 = Ick2 + DIk.
Поэтому формулу (13.5) можно переписать в виде
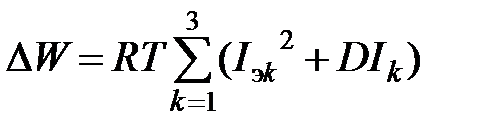 ,
,
следовательно, дисперсия может служить оценкой дополнительных потерь в питающей сети обусловленных неравномерностью графика нагрузки.Кроме того, снижение дисперсии нагрузки группы ПЭЭ позволяет уменьшить величину заявленной потребителем максимальной мощности, участвующей в максимуме нагрузки энергосистемы, и, следовательно, снизить оплату за пользование электрической энергией данным предприятием. Под заявленной мощностью имеется в виду абонируемая потребителем наибольшая получасовая электрическая мощность Р30, совпадающая с периодом максимальной нагрузки энергосистемы и определяемая по известной формуле
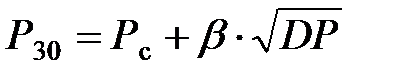 ,
,
где Рс и DP – соответственно средняя мощность и её дисперсия; коэффициент b принимается, равным 1,73.
Уменьшение заявленной мощности позволит предприятию снизить оплату за энергию.
При уменьшении дисперсии групповой нагрузки снижаются загрузки и потери в трансформаторах ГПП.
При известных графиках нагрузки N отдельных электроприёмников, дисперсию их группового графика определяют по формуле (13.3), которую можно представить в следующем виде:
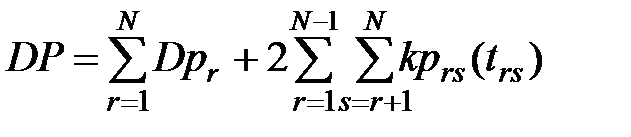 , (13.6)
, (13.6)
где Dpr – дисперсия графика отдельного r-го ПЭЭ;
kprs(trs) – взаимно корреляционная функция (ВКФ), зависящая от сдвига во времени trs графиков нагрузки r-го и s-го ПЭЭ. Под знаком суммы второго слагаемого в формуле (13.6) число ВКФ равно N (N - 1) / 2.
Дата добавления: 2016-08-06; просмотров: 1479;











