Решение задачи выравнивания группового графика сводится к определению условий, при которых его дисперсия будет минимальной.

Дисперсия группового графика является функцией режима совместной работы N электроприёмников с их индивидуальными графиками нагрузки, сдвиги между которыми и определяют, в конечном счёте, величину дисперсии. Полагая и индивидуальные графики нагрузки периодическими с периодом t_ц, ВКФ между отдельными их парами определяют по формуле:

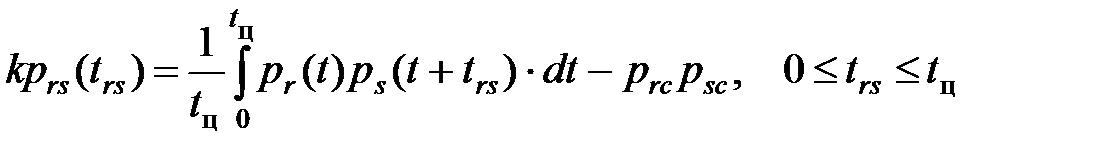
или для ступенчатых моделей

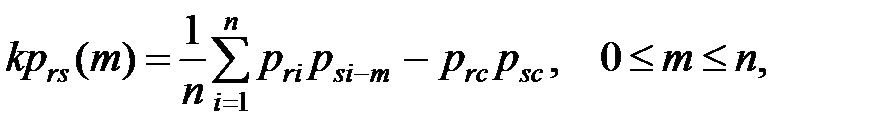(13.7)

где p_rc, p_sc – средние значения графиков нагрузки r-го и s-го ПЭЭ;

t_ц – длительность циклов, полагаемая одинаковой для r-го и s-го графиков.

Задачу выравнивания группового графика нагрузки решают с помощью аналитического или приоритетно-шагового методов. Первый метод пригоден для решения задач, если ВКФ индивидуальных графиков моделируются с допустимыми погрешностями параболами вида

,

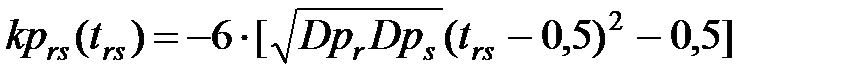где сдвиг во времени между графиками задан в относительных единицах: 0 < t_rs ≤ 1.

Приоритетно-шаговый метод может быть применён для приёмников с различными индивидуальными графиками. Выбор сдвигов производится последовательно, т.е. «шагами». В первую очередь по значениям экстремумов ВКФ выбирается сдвиг между парой графиков, имеющих наибольшее значение минимума ВКФ (приоритет) и т.д. Этим методом удобно пользоваться при небольшом количестве приёмников.