Оценка проницаемости продуктивного пласта

Породы, залегающие в недрах земли, находятся под влиянием горного давления, которое обусловлено весом пород, тектоническими силами, напором подземных вод и газов, силами тектонического движе­ния земной коры, термическими напряжениями, возникающими под влиянием тепла земных недр, пластовым давлением. В результате воз­действия на породу комплекса упомянутых сил элемент породы, выделенный из массива, может находиться в условиях сложного напряжённого состояния. Оно характеризуется тем, что результирующие векторы напряжений, действующие на грани, не являются перпендикулярами к его граням. Компоненты напряжений зависят от ориентации выделенного элементарного объёма породы в пространстве.

Элементарный объём – это физическое свойство, тот представительный объём, который характеризует свойство объёма.

Процессы, в массивах пород идут по осям, то есть по векторам напластования. А, следовательно, суммарные макроскопические свойства массивов пород: теплопроводность, электрические свойства и другие, включая и коэффициенты проницаемости – величины тензорные, зависящие от направления поля действия и степени ориентации минеральных частиц.

Рассмотрим случай линейно-горизонтальной фильтрации жидкости, направленной параллельно напластованию в пласте, состоящем из нескольких изолированных слоёв или пропластков пористой среды, разделенных между собой бесконечно тонкими непроницаемыми перегородками различной мощности и проницаемости (рис. 1.17).

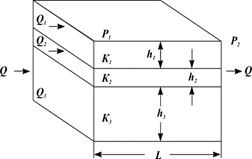
Рис. 1.17. Линейная фильтрация в пласте, состоящем из нескольких изолированных пропластков различной мощности и проницаемости

Средняя величина коэффициента проницаемости пласта будет оцениваться с учётом мощности продуктивных пропластков, через которые идёт фильтрация и вида её направления. Для данного случая она идёт параллельно напластованию:

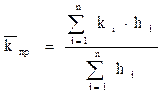, (1.23)

где 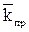– средняя проницаемость пласта;

k_i – проницаемость i-го пропластка;

h_i – мощность (высота) i-го пропластка.

Рассмотрим пример. Рассчитать величину среднего коэффициента проницаемости пласта, состоящего из нескольких изолированных пропластков для условий:

Дано: № уч-ка h_i, м k_i, мД

1 6 100

2 4,5 200

3 3 300

4 1,5 400

Найти: чему равен средний коэффициент проницаемости ( 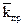) пласта?

Решение: 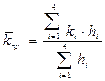= (100·6 + 200·4,5 + 300·3 + 400·1,5)/15 = 200 (мД).

При горизонтально-линейной фильтрации жидкости, направленной перпендикулярно напластованию, через пласт, имеющий несколько параллельно-последовательно расположенных изолированных зон пористой среды различной проницаемости (рис. 1.18), средняя величина коэффициента проницаемости такого пласта рассчитывается с учётом протяженности (длины) фильтрации флюидов и её направленности по уравнению (1.24).

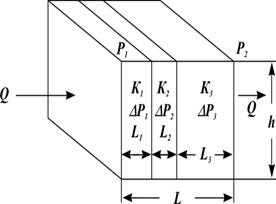
Рис. 1.18. Линейная фильтрация через пласт, имеющий несколько последовательно расположенных зон различной проницаемости

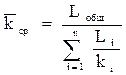, (1.24)

где 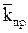– средняя проницаемость пласта;

k_i – проницаемость i-го пропластка;

L_i – длина i-го пропластка;

L_общ = ∑L_i – общая длина пласта.

Рассмотрим пример. Рассчитать для горизонтально-линейной фильтрации жидкости средний коэффициент проницаемости пласта, который имеет несколько последовательно параллельно расположенных изолированных зон различной проницаемости с учетом условий:

Дано: № уч-ка L_i, м k_i, мД

1 75 25

2 75 50

3 150 100

4 300 200

Найти: чему равен средний коэффициент проницаемости ( 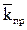) пласта?

Решение: 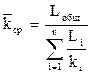= (75 + 75 + 150 + 300)/(75/25 + 75/50 +

150/100 + 300/200) = 600/7,5 = 80 (мД).

При радиальной фильтрации жидкости через пласт, имеющий несколько концентрически расположенных зон различной проницаемости (рис. 1.19), средняя величина коэффициента проницаемости для пласта оценивается с учетом радиуса контура радиальной фильтрации флюидов через продуктивные пропластки по выражению:

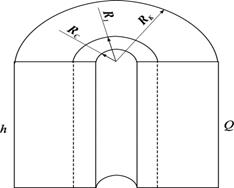
Рис. 1.19. Радиальная фильтрация через пласт, имеющий несколько концентрически расположенных зон различной проницаемости

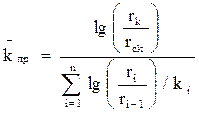, (1.25)

где 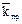– средняя проницаемость пласта;

k_i – коэффициент проницаемости i-ой зоны;

r_i – радиус i-ой зоны;

r_c – радиус скважины;

r_k – радиус контура питания.

Рассмотрим пример. Рассчитать средний коэффициент проницаемости пласта для случая радиальной фильтрации жидкости с учетом условий:

Дано: № уч-ка r_i,м k_i, мД

1 75 25

2 150 50

3 300 100

4 600 200

r_c = 0,15 м, r_k = 600 м.

Найти средний коэффициент проницаемости ( 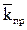) пласта?

Решение: 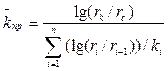=lg(600/0,15)/{[lg(75/0,15)]/25+

+ [lg(150/75)]/50 + [lg (300/150)]/100 + [lg(600/300)]/200} = 30,4 (мД).