Зависимость пористости и проницаемости от диаметра зёрен
| № п./п. | Диаметр зёрен, мм | Коэффициент пористости, % | Коэффициент проницаемости, мД |
| 0,503–0,381 | 344,81 | ||
| 0,381–0,280 | 65,89 | ||
| 0,280–0,221 | 43,46 | ||
| 0,221–0,191 | 40,91 | ||
| 0,191–0,175 | 26,36 | ||
| 0,175–0,134 | 10,19 | ||
| 0,134–0,114 | 9,93 | ||
| 0,114–0,105 | 9,26 |
Оценить качественную зависимость изменения проницаемости от размера пор в предположении, что фильтрация флюидов происходит через капиллярные поры, а пористая среда рассматривается как идеальная система, можно из соотношений законов Пуазейля и Дарси.
Уравнение Пуазейля описывает объёмную скорость течения жидкости через пористую среду, которая представляется в виде системы прямых трубок одинакового сечения длиной (L), равной длине пористой среды:
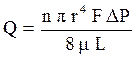 , (1.26)
, (1.26)
где n – число пор на единицу площади фильтрации;
r – радиус порового канала;
F – площадь фильтрации;
DР – перепад давления;
L – длина порового канала;
m – вязкость жидкости.
По определению (1.4) коэффициент пористости среды, через которую проходит фильтрация, можно представить следующим образом:
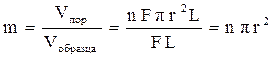 . (1.27)
. (1.27)
С учётом (1.27), уравнение Пуазейля (1.26) преобразуется в выражение:
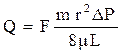 . (1.28)
. (1.28)
Сравнивая полученное нами уравнение (1.28) с уравнением Дарси (Q = k·F·∆P/μ·L) и приравняв правые части этих уравнений, сократив подобные параметры, получим выражение для искомой взаимосвязи проницаемости, пористости и радиуса порового канала:
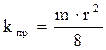 . (1.29)
. (1.29)
Анализируя полученное выражение (1.29) видно, что взаимосвязь между проницаемостью и пористостью нелинейная. Для графической линеаризации зависимости (у = а + bх) её представляют в полулогарифмических координатах → "lg (kпр) ↔ m".
Оценочные измерения показали, что радиусы пор, по которым происходит движение жидкостей, находятся в пределах от 5 до 30 мкм. Полученная корреляционная взаимосвязь (1.29) используется при проведении прогнозных и модельных расчётов коэффициентов проницаемости для образцов кернового материала с известной пористостью.
Выражение (1.29) используется и для оценки радиуса (размера) порового канала для образцов кернового материала с известными величинами пористости и проницаемости:
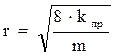 . (1.30)
. (1.30)
Если выразить проницаемость в мкм2, то и радиус поровых каналов в мкм будет рассчитываться по эмпирическому выражению:
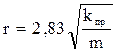 . (1.31)
. (1.31)
Уравнения (1.29–1.31) справедливы только для однородной пористой среды, например для кварцевого песка, и характеризуют взаимосвязь между пористостью, проницаемостью, радиусом порового канала. Для реальных коллекторов оценка радиуса порового канала производится с учётом структурных особенностей порового пространства пород. Обобщённым выражением для этих целей является, например, эмпирическое уравнение Ф. И. Котяхова:
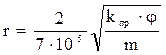 , (1.32)
, (1.32)
где r – радиус пор;
j – структурный коэффициент, учитывающий извилистость порового пространства.
Величины j оценивают экспериментально на модельных средах путём измерения электрического сопротивления пород. Как правило, значения коэффициентов j обратно пропорциональны величинам коэффициентов пористости (m). По экспериментальным данным для керамических, пористых сред при изменении пористости от 0,39 до 0,28, коэффициент j изменяется от 1,7 до 2,6.
Для приближённой оценки структурного коэффициента зернистых пород в литературе предложены различные эмпирические выражения, одно из которых представлено ниже:
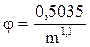 . (1.33)
. (1.33)
При проведении инженерных расчётов для известных типов коллекторов часто используют эмпирические зависимости, полученные теоретическим путём. Допустим, фильтрация идёт через поры круглого сечения и радиус порового канала известен. Тогда оценку коэффициента проницаемости при фильтрации жидкости через поры круглого сечения рассчитывают, используя взаимосвязь коэффициента проницаемости от радиуса порового канала, полученную из сопоставления уравнений Пуазейля и Дарси:
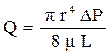 и
и 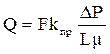 . (1.34)
. (1.34)
Причём, пористая среда представляет собой систему трубок. Общая площадь пор, через которые идет фильтрация флюидов, оценивается как F = π·r2. Отсюда, величину π можно выразить как π = F/r2.
Подставив эту величину в уравнение Пуазейля (1.34, левое выражение) и сократив одинаковые параметры в выражениях (1.34, левом и правом), получим корреляционную связь между коэффициентом проницаемости породы от радиуса порового канала:
kпр =r2/8.(1.35)
Если радиус r измеряется в см, а коэффициент проницаемости в Д (1Д ≈ 1,02·10–8 см2 или = 1,01327·10–8), то вводится соответствующий коэффициент пересчёта, равный 9,869·10–9. Тогда коэффициент проницаемости при фильтрации жидкости через капилляр или канал оценивается эмпирическим выражением:
kпр =r2/(8·9,869·10–9) = 12,5·106 ×r2. (1.36)
Для трещинного типа коллектора оценка коэффициента проницаемостипри фильтрации жидкости только через поры-трещиныосуществляется с использованиемвзаимосвязи коэффициента проницаемости от высоты поровой трещины, полученной из соотношений уравнений Дарси и Буссинеска.
По уравнению Буссинеска, потеря давления при течении жидкости через щель очень малой высоты описывается соотношением:
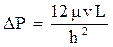 , (1.37)
, (1.37)
где v – линейная скорость фильтрации жидкости;
h – высота трещины.
Выделив из уравнения Дарси величину перепада давления
∆P = v·μ·L/kпр и приравняв правые части рассматриваемых уравнений, после сокращения одинаковых параметров получим выражение для оценки коэффициента проницаемости:
kпр = h2/12. (1.38)
С учетом того, что h измеряется в см, а коэффициент проницаемости в Д, вводится соответствующий коэффициент пересчёта, равный 9,869·10–9. Тогда коэффициент проницаемости пористой среды при фильтрации жидкости в ней через трещину оценивается:
kпр =h2/(12·9,869·10–9) = 84,4·105·h2. (1.39)
Уравнения (1.36 и 1.39) используются для теоретической оценки коэффициентов проницаемости для конкретного вида пор.
Рассмотрим пример.Через кубик породы размером 10·10·10 см3 проницаемостью в 10 мД фильтруется жидкость при линейной режиме течения вязкостью 1 сПз, при градиенте давления (∆Р/∆L) = 25 кПа/м (0,25 кПа/см). Определить дебит фильтрующейся жидкости?
Решение. Рассмотренный случай описывает капиллярный вид фильтрации. То есть, фильтрация равномерная и проходит через всю площадь образца, имеющего капиллярную пористость. Дебит (Q1) составит
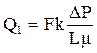 = 100·0,01·(0,25/1) = 0,25 см3/с.
= 100·0,01·(0,25/1) = 0,25 см3/с.
Если в этом кубике будет один канал диаметром 0,2 мм той же длины, что и кубик, то при том же градиенте давления дебит фильтрующейся жидкости через этот канал будет:
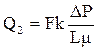 = 12,5·106·(0,02/2)2·π·(0,02/2)2·0,25 = 0,1 см3/с.
= 12,5·106·(0,02/2)2·π·(0,02/2)2·0,25 = 0,1 см3/с.
Следовательно, при наличии в кубике одного канала и капиллярной пористости, то есть при наличии неравномерной фильтрации, суммарный дебит (Q3) фильтрующейся жидкости составит
Q3 = Q2 + Q1 = 0,1 + 0,25 = 0,35 (см3/с).
Суммарный дебит (Q3) имеет величину на 40 % больше, чем при капиллярной фильтрации (Q1).
Если в кубике вместо канала имеется трещина высотой 0,2 мм и шириной 10 см, её влияние на общий дебит жидкости, фильтрующейся через породу, будет существенным:
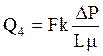 = (84,4·105·(0,02)2·0,02·10·0,25)/1 = 168,8 см3/с.
= (84,4·105·(0,02)2·0,02·10·0,25)/1 = 168,8 см3/с.
Суммарный дебит (Q5) с учётом и капиллярной фильтрации (Q1) составит
Q5 = Q4 + Q1 = 168,8 + 0,25 = 169,05 (см3/с).
По сравнению с первым случаем (Q1) суммарный дебит увеличился в 675 раз.
Пример свидетельствует о большом влиянии наличия каналов и особенно трещин в породе на объём фильтрующейся жидкости. В коллекторах смешанного типа (уравнение 1.7) наличие трещин существенно увеличивает проницаемость продуктивных пластов:
mтрещ<< mгран → kпр/трещ >> kпр/гран. (1.40)
На практике проницаемость породы определяют в лабораторных условиях по керновому материалу.
Виды проницаемости
При разработке нефтяных и газовых месторождений встречаются различные виды фильтрационных потоков: движение нефти или газа, совместное движение двух или трёхфазного потока. В пористой среде одновременно движутся нефть, газ и вода или их смеси. В связи с этим проницаемость одной и той же пористой среды для одной фазы (жидкости или газа) будет изменяться в зависимости от соотношения компонентов в смеси. Поэтому для характеристики проницаемости нефтесодержащих пород введены понятия абсолютной, фазовой (эффективной) и относительной фазовой проницаемостей.
Проницаемость абсолютная (физическая) характеризует проницаемость пористой среды для газа или однородной жидкости при выполнении следующих условий:
· отсутствие физико-химического взаимодействия между пористой средой и этим газом или жидкостью, фаза химически инертна по отношению к породе;
· полное заполнение всех пор среды этим газом или жидкостью.
Абсолютная проницаемость характеризует фильтрационную способность горной породы для инертного в физико-химическом отношении флюида. Для реальных продуктивных нефтяных пластов эти условия не выполняются.
Проницаемость фазовая(эффективная)– это проницаемость пористой среды для данного газа или жидкости при одновременной фильтрации многофазных систем. То есть при наличии в порах другой фазы (жидкости или газа) или других фаз (газ–нефть, нефть–вода, вода–газ, газ–нефть–вода) независимо от того, находятся они в статическом состоянии (например, капиллярно связанная вода) или принимают участие в совместной фильтрации. Величины фазовых проницаемостей зависят не только от физических свойств пород, но и от степени насыщенности порового пространства жидкостями или газом и от их физико-химических свойств. При фильтрации смесей коэффициент фазовой проницаемости намного меньше коэффициента абсолютной проницаемости и неодинаков для пласта в целом.
Относительная фазовая проницаемость определяется отношением величины фазовой проницаемости к величине абсолютной для той же породы. Относительные проницаемости (k', % или в дол. ед.) породы для нефти и воды (газа аналогично) оцениваются как:
k'н = (kн/k)·100, %; k'в = (kв/k)·100, %; (1.41)
где kн и kв – фазовые проницаемости для нефти и воды;
k – абсолютная проницаемость породы.
Фазовая и относительная фазовая проницаемости горных пород зависят от степени насыщения (насыщенности) породы флюидами, градиента давления, соотношения фаз, физико-химических свойств породы и флюидов и определяются экспериментально.
Дата добавления: 2019-02-08; просмотров: 1898;











