Осмотическое давление растворов

В качестве примера одного из общих свойств растворов полимеров, зависящих от числа частиц, т. е. коллигативных свойств, рассмотрим осмотическое давление раствора полимера. Измерение осмотического давления позволяет косвенно определить понижение упругости пара растворителя над раствором по сравнению с чистым растворителем 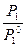и активность растворителя 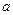. Рассмотрим схему осмотического опыта (рис. 13.7).

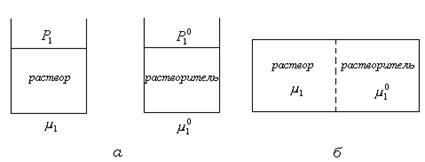
Рис.13.7. Схемы осмотического опыта: ( 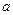) – равновесие устанавливается через газовую фазу; (б) равновесие устанавливается через жидкую фазу.

Коллигативные свойства сильно разбавленных растворов проявляются в том, что работа отделения растворенного компонента от растворителя пропорциональна числу растворенных частиц, не зависит от их природы и описывается законом Рауля.

В один из открытых сосудов нальем раствор полимера, в другой – чистый растворитель, и поместим эти сосуды в замкнутое пространство (рис. 13.7. 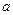). По закону Рауля упругость пара растворителя над чистым растворителем 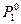больше, чем упругость пара растворителя над раствором: 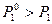. Поэтому произойдет изотермическая перегонка растворителя из сосуда с чистым растворителем в сосуд с раствором. При этом станут равными химические потенциалы растворителя в чистом растворителе и растворе.

В сосуде, разделенном полупроницаемой мембраной, в одной половине которого находится чистый растворитель, а в другой раствор полимера (рис. 13.7.б), также произойдет выравнивание химического потенциала растворителя, но через жидкую фазу. Выравнивание химического потенциала растворителя в обеих частях сосуда связано с осмотическим давлением системы.

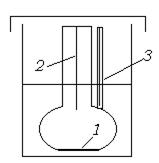
Рис. 13.8. Схема осмометра.

1 – полупроницаемая мембрана; 2 – Измерительный капилляр; 3 – Контрольный капилляр.

Осмотическое давление – это сила, приходящаяся на единицу площади мембраны, которая заставляет растворитель проникать в раствор и является результатом взаимодействия между компонентами системы. Осмометр (рис.13.8) состоит из ячейки, основой которой служит полупроницаемая мембрана, и двух капилляров (рис.13.8), измерительного и контрольного. В ячейку заливается раствор полимера, в широкий сосуд – чистый растворитель. При установлении равновесия высот поднятия уровня жидкости в капилляре пропорциональна осмотическому давлению. Отметим, что мембрана в осмотическом опыте не имеет принципиального значения и служит рабочим средством для установления равновесия. При отсутствии мембраны равновесие все равно установилось бы через газовою фазу, но для этого потребовалось бы много времени из-за малого сечения капилляра. При равновесии упругость пара растворителя над чистым растворителем на высоте 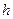становится равной упругости пара растворителя над раствором на высоте 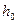. Растворение устанавливается вследствие гипсометрического закона:

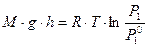(13.8)

Между осмотическим давлением раствора и молекулярной массой полимера существует зависимость.

Для идеальных растворов по закону Вант-Гоффа:

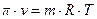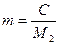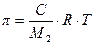; ; (13.9)

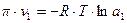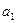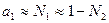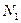т.е. должны соблюдаться пропорциональность между осмотическим давлением и концентрацией. Для неидеальных растворов при равновесии выполняется условие: , где – активность растворителя. В разбавленных растворах , где и 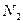– мольные доли растворителя и полимера соответственно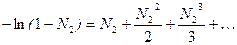

Разлагая выражение для осмотического давления в ряд, получим соотношение, аналогичное вириальному разложению для газов:

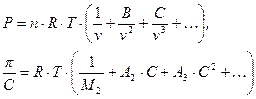(13.10)

Коэффициенты при членах этого выражения называются вириальными коэффициентами.

В разбавленных растворах полимеров вследствие малой концентрации ее квадратом можно пренебречь, и выражение (10) приобретет вид:

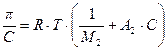(13.11)

Для определения молекулярной массы строят зависимость 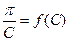, экстраполируют эту зависимость к нулевой концентрации и получают величину, обратную молекулярной массе полимера (рис.13.9). Угол наклона этой зависимости позволяет определить значение второго вириального коэффициента .

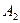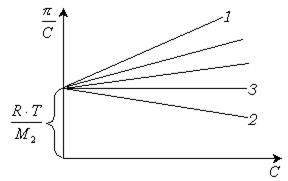
Рис. 13.9 Зависимость осмотического давления растворов от концентрации: 1 - хороший растворитель, 2 - плохой растворитель, 3 - идеальный растворитель