Правила коагуляции электролитами.
Коагуляцию вызывают все электролиты.
1. Коагулирующим действием обладает ион, противоположный по знаку заряду частицы.
2. Коагуляция начинается при достижении критической концентрации, называемой порогом коагуляции ( 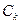 ).
).
3. Коагулирующая сила иона увеличивается при увеличении валентности иона согласно правилу Шульца-Гарди: 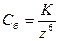 , где
, где  – порог быстрой коагуляции,
– порог быстрой коагуляции, 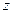 – валентность иона.
– валентность иона.
4. Коагулирующая сила ионов одинаковой валентности увеличивается при увеличении радиуса иона.
5. Коагуляция начинается не в изоэлектрической точке, а при критическом значении 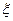 -потенциала, равном 25-40 мВ.
-потенциала, равном 25-40 мВ.
6. В осадках, получаемых при коагуляции электролитами, всегда присутствуют ионы, вызывающие ее.
XII. Структурно–механические свойства дисперсных систем
Основные понятия. Реология как метод исследования структуры дисперсных систем
Под структурой тел обычно понимают пространственное взаимное расположение составных частей тела: атомов, молекул мелких частиц. Образование структур в дисперсных системах с жидкой дисперсной средой связано с коагуляцией, т. е. слипанием, агрегированием мелких частиц в более крупные вплоть до образования осадка (коагулюма).
В результате структурообразования свободнодисперсная система переходит в связнодисперсную. Появление и характер структур как правило, определяются по изменению механических свойств, таких, как вязкости, упругости, прочности, пластичности. Так как эти свойства непосредственно связаны со структурой тел, их называют структурно-механическими. Структурно-механические свойства могут быть изучены методами реологии – науки о деформациях и течении материальных систем.
Реология изучает механические свойства систем через деформации под действием внешних напряжений. В коллоидной химии методы реологии используются для исследования структуры и вязкости дисперсных систем.
Термин деформация означает относительное смещение точек системы, при котором не нарушается ее сплошность. Упругие (обратимые) деформации делятся на объемные (растяжение, сжатие), сдвиговые и деформации кручения. Количественно они характеризуется относительными величинами.
Схематическое изображение деформации сдвига показано на рис. 12.1
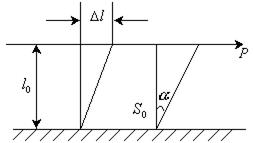
Рис. 12.1. Схематическое изображение деформации сдвига.
На прямоугольный элемент высотой 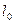 и площадью основания
и площадью основания  тангенциально действует сила
тангенциально действует сила  . Элемент деформируется на величину
. Элемент деформируется на величину 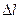 . Касательное напряжение
. Касательное напряжение 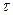 равно
равно 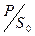 . Относительная деформация сдвига
. Относительная деформация сдвига 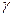 равна
равна 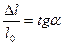 .
.
Для твердого тела зависимость деформации от напряжения устанавливается законом Гука: 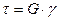 , где
, где 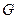 - модуль сдвига. Для жидкости деформация развивается во времени, она неопределенна, т. к. жидкость течет. Поэтому находят зависимость между касательным напряжением
- модуль сдвига. Для жидкости деформация развивается во времени, она неопределенна, т. к. жидкость течет. Поэтому находят зависимость между касательным напряжением 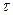 и скоростью деформации
и скоростью деформации 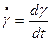 .
.
Дата добавления: 2020-11-18; просмотров: 595;











