Влияние температуры и разбавления на ДЭС
Влияние температуры и разбавления на ДЭС показано на рис. 10.20.
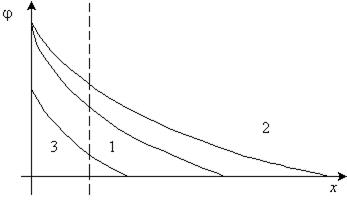
Рис. 10.21. Влияние нагревания и разбавления на ДЭС. 1 – 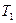 (
( 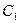 ); 2 –
); 2 – 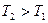 (
( 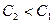 ); 3 –
); 3 – 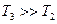 (
(  ).
).
В ряду 1–2–3 происходит повышение температуры или уменьшение концентрации. Потенциалопределяющие ионы адсорбированы прочно, а противоионы находятся в тепловом движении. При нагревании или разбавлении происходит изменение равновесия системы вызывающие расширение диффузной части ДЭС, и 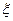 - потенциал увеличивается (кривая 2).
- потенциал увеличивается (кривая 2).
При сильном повышении температуры или сильном разбавлении происходит сильная десорбция потенциалопределяющих ионов, что приводит к уменьшению 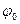 и
и 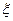 - потенциала (кривая 3). Действие нагревания или разбавления может вызвать коагуляцию коллоидной системы.
- потенциала (кривая 3). Действие нагревания или разбавления может вызвать коагуляцию коллоидной системы.
XI. Устойчивость и коагуляция коллойдных систем
11.1. Понятие об устойчивости
Устойчивость коллоидных систем является одной из центральных вопросов коллоидной химии, ибо она определяет возможность и время существования коллоидных систем. Время существования коллоидных систем изменяется в очень широких пределах. Так, золи золота, очищенные путем диализа, приготовленные еще Фарадеем, существуют еще и в настоящее время, т. е. более 100 лет. Эмульсия масла (например, подсолнечного, вазелинового) в воде, расслаивается в течение нескольких минут. Под устойчивостью, или стабильностью коллоидной системы мы понимаем способность системы сохранять свое первоначальное состояние. При этом необходимо учитывать, что устойчивая коллоидная система должна сохранять во времени два параметра; равновесное распределение частиц в среде и степень их дисперсности. С этим связаны два вида устойчивости коллоидных систем: седиментационная, или кинетическая и агрегативная. Седиментационная устойчивость рассматривается по отношению к силе тяжести и определяется установлением равновесия между силой тяжести, приводящей к оседанию частиц, и диффузией под действием броуновского движения, приводящей к их равномерному распределению. Вследствие этого частицы распределяются в объеме по гипсометрическому закону.
Агрегативная устойчивость определяет способность системы к сохранению степени дисперсности и индивидуальности частиц. Коллоидные системы агрегативны неустойчивы, т. к. в них протекают процессы слипания, коагуляции частиц с образованием агрегатов, представляющих собой ансамбль частиц. Если силы взаимодействия между частицами малы, то слипание частиц происходит обратимо и называется флокуляцией. Если силы взаимодействия между частицами велики, то происходит процесс необратимой коагуляции. В случае жидкой дисперсной фазы объединение двух капель в одну называется коалесценцией.
Крупные частицы оседают быстрее, чем мелкие, т.е. коагуляция приводит к уменьшению седиментационной устойчивости системы. В то же время первую стадию коагуляции следует рассматривать как переход к более устойчивому состоянию системы, что следует из термодинамического рассмотрения процесса.
При термодинамическом рассмотрении устойчивости и коагуляции следует учитывать, что при слипании частиц происходит уменьшение свободной поверхностной энергии 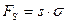 . Это происходит по тому, что при слипании происходит уменьшение поверхности частицы
. Это происходит по тому, что при слипании происходит уменьшение поверхности частицы 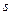 (рис. 11.1).
(рис. 11.1).

Рис. 11.1. Образование фазового контакта между частицами.

Вследствие уменьшения поверхности свободная поверхностная энергия уменьшается, и система переходит в более устойчивое состояние. При таком типе взаимодействия частицы одной фазы непосредственно контактируют между собой, т. е. образуются фазовые контакты. Их образование происходит двумя путями: поджатием при плавлении и выделением новой фазы.
Если слипание происходит через прослойки среды, то уменьшается поверхностное натяжение в прослойке (рис. 11.2). В этом случае коагуляция происходит без непосредственного контакта частиц, когда взаимодействие осуществляется через прослойку жидкости.
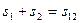
При слипании суммарная поверхность исходных частиц сохраняется постоянной.
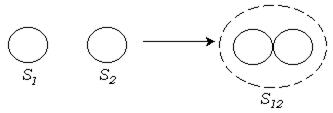
Рис. 11.2. Образование коагуляционного контакта между частицами.
В зоне контакта происходит уменьшение поверхностного натяжения вследствие изменения состояния жидкости в прослойке. Поэтому свободная поверхностная энергия уменьшается, и устойчивость увеличивается. Контакты такого типа называются коагуляционными. Коагуляционные контакты склонны к тиксотропии и пластичности. В реальных условиях при коагуляции часто образуются контакты переходного типа, называемые точечными.
11.2. Расклинивающее давление
Термодинамический подход к агрегативной устойчивости включает представления о расклинивающем давлении, развитые Б.В.Дерягиным в 1935 г. Расклинивающее давление возникает между частицами и любыми поверхностями, разделенными прослойкой жидкости. Термин «расклинивающее давление» отражает упругие свойства сольватных прослоек между твердыми поверхностями, которые действуют механически, наподобие клина, как бы раздвигая, расклинивая эти поверхности. Рассмотрим физический смысл расклинивающего давления с точки зрения термодинамики. Для этого представим две твердые поверхности, разделенные жидкой фазой. На этих поверхностях образованы граничные слои толщиной  и
и  .
.
В случае толстых прослоек, когда расстояние между поверхностями 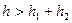 , давления в прослойке,
, давления в прослойке, 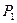 и в фазе, из которой образована прослойка,
и в фазе, из которой образована прослойка, 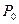 равны, а их разность, обозначенная как
равны, а их разность, обозначенная как 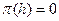 . Химический потенциал жидкости в объеме и в прослойке одинаков
. Химический потенциал жидкости в объеме и в прослойке одинаков 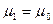 .
.
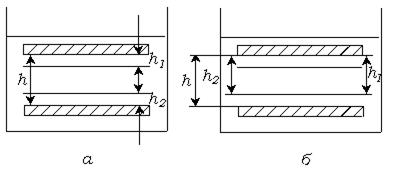
Рис. 11.3. Толстые ( 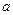 ) и тонкие (
) и тонкие ( 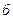 ) прослойки между твердыми поверхностями.
) прослойки между твердыми поверхностями.
При уменьшении толщин прослойки жидкости, когда  , граничные слои перекрываются, и
, граничные слои перекрываются, и 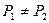 .
.
Возникает расклинивающее давление:
 (11.1)
(11.1)
Расклинивающее давление – это избыточное давление, которое возникает в межфазной прослойке жидкости при достаточном ее утоньшении, которое препятствует утоньшению прослойки и равно разности давлений в прослойке и в фазе, из которой образовалась прослойка.
Для гетерогенной системы, состоящей из двух поверхностей и прослойки между ними, запишем обобщенное уравнение первого и второго начала термодинамики. Для толстых прослоек в обобщенное уравнение 1 и 2 начал термодинамики входят поверхностные энергии обеих межфазных поверхностей, т. е. 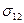 и
и 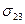 .
.
Избыточные термодинамические функции тонких прослоек зависят от толщины прослойки 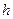 . Избыточная энергия Гиббса для тонкой прослойки равна:
. Избыточная энергия Гиббса для тонкой прослойки равна:
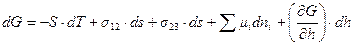 (11.2)
(11.2)
где 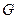 ,
, 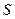 ,
, 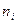 – суммарные для обеих поверхностей величины. Последний член уравнения (11.2) отражает вклад расклинивающего давления в общую энергию системы. Его можно рассматривать как давление, которое надо приложить к прослойке, чтобы сохранить ее равновесную толщину. С учетом уравнения (11.1) выражение для расклинивающего давления можно записать в следующем виде:
– суммарные для обеих поверхностей величины. Последний член уравнения (11.2) отражает вклад расклинивающего давления в общую энергию системы. Его можно рассматривать как давление, которое надо приложить к прослойке, чтобы сохранить ее равновесную толщину. С учетом уравнения (11.1) выражение для расклинивающего давления можно записать в следующем виде:
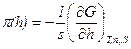 (11.3)
(11.3)
Следовательно, расклинивающее давление – это приращение энергии Гиббса на данном расстоянии между пластинами, пересчитанное на единицу толщины прослойки и отнесенное к единице площади перекрывания поверхностных слоев.
Расклинивающее давление может быть положительным и отрицательным. Отталкивание поверхностных слоев приводит к положительному расклинивающему давлению, соответствующему уменьшению энергии Гиббса с увеличением толщины прослойки. Поэтому перед производной  стоит знак минус.
стоит знак минус.
В соответствии с природой действующих сил расклинивающее давление имеет следующие компоненты: молекулярную, структурную, электростатическую, адсорбционную и стерическую (энтропийную). Каждая из этих компонент соответствует определенному фактору устойчивости коллоидных систем.
Молекулярная компонента связана с действием межмолекулярных Ван-дер-ваальсовых сил. Положительное расклинивающее давление обусловлено увеличением потенциальной энергии молекул или ионов в тонких прослойках. При большой толщине прослойки существует равновесие между прослойкой и объемом, энергия молекул в прослойке равна их энергии в объеме (рис. 11.4). Если толщина прослойки меньше двух радиусов действия межмолекулярных сил (  ), то молекулы в прослойке взаимодействуют с меньшим числом молекул, чем в объеме, и их энергия будет больше. В прослойке находятся те молекулы, энергия которых приближается к энергии молекул на поверхности, т. е. молекулы с избытком энергии. Эти молекулы стремятся уменьшить избыточную поверхностную энергию и втягивают из объема молекулы с меньшей энергией. Это приводит к возникновению положительного расклинивающего давления.
), то молекулы в прослойке взаимодействуют с меньшим числом молекул, чем в объеме, и их энергия будет больше. В прослойке находятся те молекулы, энергия которых приближается к энергии молекул на поверхности, т. е. молекулы с избытком энергии. Эти молекулы стремятся уменьшить избыточную поверхностную энергию и втягивают из объема молекулы с меньшей энергией. Это приводит к возникновению положительного расклинивающего давления.
Отрицательное расклинивающее давление, соответствующее притяжению поверхностных слоев и сжатию прослойки, возникает, когда межмолекулярные Ван-дер-ваальсовы силы притяжения как внутри фазы, так и между фазами превышают силы отталкивания.
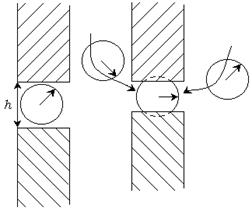
Рис. 11.4. Расклинивающее давление.
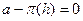 ;
; 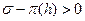
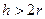 ;
; 
Структурная компонента расклинивающего давления состоит в том, что сольватные поверхностные слои обладают повышенной вязкостью и прочностью и поэтому вытеснение жидкости из прослойки затрудняется. Поверхностные слои, состоящие из адсорбированных полимерных молекул, ориентированы и представляют собой твердые пленки, обладающие высокой поверхностной прочностью. Поэтому они предохраняют частицы от слипания, стабилизируют систему. Наибольшая устойчивость возникает при достижении насыщенного адсорбционного слоя на поверхности частицы. Особенно большой прочностью обладают адсорбционные слои полимеров, белков и некоторых ПАВ.
Электростатическая компонента проявляется при наличии заряда поверхностей и состоит в образовании в прослойке заряда, одноименного с зарядом поверхности, что увеличивает отталкивание поверхностей. Это наблюдается при перекрывании двойных электрических слоев.
Если нет перекрывания двойных электрических слоев частиц, то нет отталкивания между ними (рис. 11.5 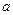 ). Силы отталкивания возникают только при перекрывании ионной атмосферы коллоидных частиц, т. е. диффузных слоев противоионов. (рис. 11.5.
). Силы отталкивания возникают только при перекрывании ионной атмосферы коллоидных частиц, т. е. диффузных слоев противоионов. (рис. 11.5. 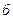 )
)

Рис. 11.5. Перекрывание двойных электрических слоев.
При этом в зоне перекрывания происходит перераспределение ионов с изменением их концентрации, вследствие чего появляются дополнительные электростатические силы отталкивания.
Пока ДЭС не перекрываются (рис. 11.6. 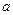 ), потенциал в середине слоя между пластинами равен нулю.
), потенциал в середине слоя между пластинами равен нулю.
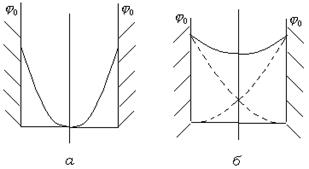
Рис. 11.6. Изменение потенциала поверхности между пластинами при отсутствии перекрывания ( 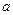 ) и при перекрывании (
) и при перекрывании ( 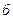 ) ДЭС.
) ДЭС.
При уменьшении расстояния между частицами и перекрывании ДЭС потенциал между частицами нигде не достигает нулевого значения (рис. 11.6. 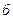 ). Наличие в прослойке потенциала того же знака, что и на поверхности, приводит к отталкиванию частиц.
). Наличие в прослойке потенциала того же знака, что и на поверхности, приводит к отталкиванию частиц.
Адсорбционная компонента расклинивающего давления связана с неравномерным распределением растворенного вещества в прослойке, т. е. изменением состава поверхностного слоя по сравнению с объемом.
Стерическая компонента возникает в результате перекрывания адсорбционных слоев ПАВ с длинными углеводородными радикалами и полимеров. Это связано с тем, что в тонких прослойках число конформаций гибких радикалов меньше, чем при большом расстоянии между частицами, и энтропия системы также меньше. Поэтому за счет энтропийного фактора частицы отталкиваются и сохраняют свою индивидуальность. Следует иметь в виду, что энтропийный фактор устойчивости коллоидных систем имеет и другое проявление: при дроблении энтропия системы увеличивается и ее устойчивость повышается. Если увеличение энтропии перекрывает увеличение поверхностной энергии за счет увеличения поверхности, то происходит самопроизвольное диспергирование.
11.3. Теория агрегативной устойчивости и коагуляции лиофобных дисперсных систем (теория ДЛФО)
В теории устойчивости лиофобных дисперсных систем, разработанной Дерягиным, Ландау, Фервеем и Овербеком и называемой теорией ДЛФО, рассматривается действие электрических и молекулярных сил. Другие факторы устойчивости не поддаются количественному рассмотрению и не учитываются в теории ДЛФО. В теории ДЛФО гидрофобные коллоиды рассматриваются как термодинамически неустойчивые системы. Их временная агрегативная устойчивость определяется присутствием энергетического или силового барьера при сближении частиц, и имеет чисто кинетический характер. Тепловое движение молекул среды, вызывающее броуновское движение частиц, является дестабилизирующим фактором, перемещая частицы в зону действия Ван-дер-Вальсовых сил притяжения.
11.4. Кинетический подход к устойчивости дисперсных систем
Проблема образования устойчивых коллоидных систем имеет общность с проблемой растворения в классической химии. Два газа всегда образуют газовый раствор, т. к. газы неограниченно смешиваются вследствие слабых межмолекулярных сил. В конденсированных фазах между молекулами действуют значительные силы, препятствующие испарению. При растворении или диспергировании силы между одинаковыми молекулами или частицами как фазы так и среды должны быть преодолены, и вступают в действие силы между разнородными молекулами или частицами. Если последние много больше первых, то это благоприятствует диспергированию, если меньше, то наоборот, диспергирование затрудняется, протекает коагуляция. Таким образом, устойчивость дисперсий определяется природой сил, действующих между частицами.
При кинетическом рассмотрении устойчивости принимается во внимание баланс сил притяжения и отталкивания между частицами. Процесс слипания определяется преобладанием сил притяжения над силами отталкивания. При этом частицы теряют свою индивидуальность, и вначале образуются агрегаты частиц, а затем макрофаза.
11.5. Природа сил, действующих между частицами.
Силы притяжения.
Силы притяжениямежду частицами по своей природе являются силами Ван-дер-ваальса. Известно, что силы Ван-дер-Ваальса имеют тройственную природу. Если молекулы являются электростатическими диполями, то между разноименно заряженными концами действуют электростатические (кулоновские) силы притяжения, называемые ориентационными. Энергия ориентационного притяжения убывает обратно пропорционально шестой степени расстояния между диполями.
Если неполярную молекулу поместить в электрическое поле, образованное полярной молекулой, то в неполярной молекуле наводится (индуцируется) дипольный момент. Молекулы начинают взаимодействовать друг с другом. Эта энергия называется энергией индукционного взаимодействия.
К третьему типу сил межмолекулярного взаимодействия относятся дисперсионные, или лондоновские силы. Они возникают вследствие того, что нейтральные атомы представляют системы колеблющихся зарядов вследствие наличия положительного заряженного ядра и отрицательно заряженных электронов. Причиной дисперсионных сил является квантово-механический эффект, связанный с флуктуациями электрических полей атомов и молекул. Эти флуктуации происходят на ультрафиолетовых частотах и приводят к возникновению переменного диполя, способного наводить диполи в других молекулах. Дисперсионное взаимодействие синхронно с несколькими молекулами без взаимной конкуренции, в отличие от ориентационных и индукционных сил, при действии которых наблюдается конкуренция между разными диполями. Если два диполя расположены оптимально друг к другу, то они не могут быть расположены оптимально по отношению к третьему диполю.
Дисперсионные силы являются наиболее универсальными силами, определяющими энергию притяжения. Для молекул они также убывают пропорционально шестой степени расстояния между атомами. Энергия ориентационного, индукционного и дисперсионного взаимодействия зависит от дипольного момента молекул 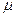 , поляризуемости атомов или молекул
, поляризуемости атомов или молекул  ,
, 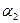 , характеристических энергий
, характеристических энергий 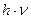 ,
, 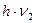 и расстояний между молекулами
и расстояний между молекулами 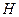 и определяется выражениями:
и определяется выражениями:
 (11.4)
(11.4)
Дисперсионные силы между частицами действуют на большем расстоянии, чем между молекулами, т. е. являются дальнодействующими. Причиной дальнодействия дисперсионных сил между частицами является их аддитивность. Для частицы, представляющей собой ансамбль атомов и молекул, дисперсионные силы, действующие между многими атомами, складываются. Энергия притяжения между частицами может быть подсчитана как сумма взаимодействий молекул, входящих в разные частицы. Благодаря аддитивности лондоновских сил энергия взаимодействия между частицами гораздо медленнее убывает с расстоянием, чем энергия взаимодействия между молекулами.
Соответствующая теория связана с эффектом электромагнитного запаздывания, который основан на том, что флуктуирующие электромагнитные поля атомов распространяются со скоростью света в рассматриваемой среде. При частоте 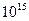
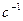 за один период свет проходит расстояние около
за один период свет проходит расстояние около 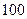
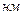 . Если расстояние между атомами превышает
. Если расстояние между атомами превышает 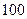
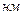 , то происходит изменение фазы колебания прежде, чем электромагнитная волна дойдет от одного атома до следующего. Электромагнитные волны, исходящие от атомов, разделенных расстоянием более
, то происходит изменение фазы колебания прежде, чем электромагнитная волна дойдет от одного атома до следующего. Электромагнитные волны, исходящие от атомов, разделенных расстоянием более 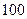
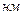 , не совпадают по фазе, имеют разность фаз, близкую к
, не совпадают по фазе, имеют разность фаз, близкую к  , что приводит к ослаблению взаимодействия. Это явление называется электромагнитным запаздыванием. Соответствующая теория приводит к выводу, что энергия взаимодействия между частицами является степенной функцией расстояния и изменяется обратно пропорционально некоторой степени расстояния между частицами (
, что приводит к ослаблению взаимодействия. Это явление называется электромагнитным запаздыванием. Соответствующая теория приводит к выводу, что энергия взаимодействия между частицами является степенной функцией расстояния и изменяется обратно пропорционально некоторой степени расстояния между частицами ( 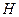 ). Показатель степени зависит от формы поверхности и от расстояния между ними. Для двух сфер радиусом
). Показатель степени зависит от формы поверхности и от расстояния между ними. Для двух сфер радиусом 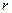 , находящихся друг от друга на расстоянии
, находящихся друг от друга на расстоянии 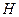 , составляющем величину от 10 до 20
, составляющем величину от 10 до 20 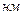 и при условии
и при условии 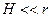 лондоновская энергия притяжения
лондоновская энергия притяжения 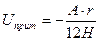 , где величина
, где величина 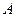 является константой молекулярного взаимодействия и называется константой Гамакера. Она учитывает природу взаимодействующих тел и выражается в единицах измерения энергии. Значение константы Гамакера в вакууме обычно составляет
является константой молекулярного взаимодействия и называется константой Гамакера. Она учитывает природу взаимодействующих тел и выражается в единицах измерения энергии. Значение константы Гамакера в вакууме обычно составляет 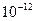
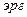 (
( 
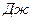 ). Константа Гамакера зависит от числа атомов в единице объема и поляризуемости молекул. Значение этой константы складывается из отдельных констант, характеризующих адгезионное и когезионное взаимодействие.
). Константа Гамакера зависит от числа атомов в единице объема и поляризуемости молекул. Значение этой константы складывается из отдельных констант, характеризующих адгезионное и когезионное взаимодействие.
В жидкости значение энергии притяжения меньше, чем в вакууме. Значение эффективной константы Гамакера определяется выражением  где индексы 1 и 2 относятся к среде и частице. Когда частица и среда химически подобны, энергия притяжения мала, т. к. значения
где индексы 1 и 2 относятся к среде и частице. Когда частица и среда химически подобны, энергия притяжения мала, т. к. значения 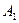 и
и 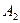 близки, и
близки, и 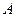 мала.
мала.
Силы притяжения не зависят от перемены мест фазы и среды. Два воздушных пузырька в воде так же сильно притягиваются друг к другу, как две капли воды того же размера в воздухе.
Для двух параллельных полубесконечных пластин энергия притяжения равна:
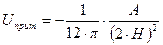 (11.5)
(11.5)
где 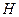 - расстояние между пластинами. Уравнение (11.5) применимо для расстояний не больше
- расстояние между пластинами. Уравнение (11.5) применимо для расстояний не больше 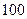
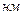 . При больших расстояниях на дисперсионное взаимодействие влияет эффект электромагнитного запаздывания. При частотах
. При больших расстояниях на дисперсионное взаимодействие влияет эффект электромагнитного запаздывания. При частотах 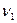 и
и  , близких к
, близких к 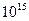
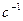 и расстояних порядка
и расстояних порядка 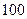
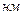 волны, излучаемые разными атомами, имеют разность фаз, близкую к p, что приводит к ослаблению взаимодействия, и выражение для энергии притяжения имеет вид:
волны, излучаемые разными атомами, имеют разность фаз, близкую к p, что приводит к ослаблению взаимодействия, и выражение для энергии притяжения имеет вид:
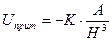 (11.6)
(11.6)
Следует отметить, что при 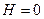 энергия притяжения частиц
энергия притяжения частиц  . При рассмотрении сил, действующих между частицами, силы притяжения обычно принимают отрицательными, силы отталкивания – положительными. Поэтому изменение энергии притяжения в зависимости от расстояния между частицами изображается так, как это показано на рис. 11.7.
. При рассмотрении сил, действующих между частицами, силы притяжения обычно принимают отрицательными, силы отталкивания – положительными. Поэтому изменение энергии притяжения в зависимости от расстояния между частицами изображается так, как это показано на рис. 11.7.

Рис. 11.7. Изменение энергии притяжения в зависимости от расстояния между частицами.
Силы отталкивания
Долговечность лиофобных систем говорит о существовании сил отталкивания между частицами. Силы отталкивания, действующие между частицами, приводят к повышению устойчивости коллоидных систем, являются факторами устойчивости. Они имеют различную природу и соответствуют различным компонентам расклинивающего давления. Если стабилизатором является электролит, и имеется двойной электрический слой, то действует электростатический фактор устойчивости. Отталкивание между частицами нельзя рассматривать как отталкивание между одноименно заряженными точечными зарядами, и силы отталкивания нельзя рассчитать по закону Кулона 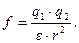 Силы отталкивания возникают за счет перекрывания двойных электрических слоев, и когда происходит нарушение симметрии распределения ионов при
Силы отталкивания возникают за счет перекрывания двойных электрических слоев, и когда происходит нарушение симметрии распределения ионов при 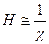 .
.
Б.В.Дерягин установил экспоненциальный закон изменения электрических сил, определяющих отталкивание частиц, с расстоянием
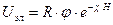 (11.7)
(11.7)
где c - величина обратная толщине ДЭС.
В отличие от энергии притяжения при 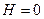 ,
, 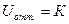 .
.
Зависимость энергии отталкивания от расстояния между частицами изображена на рис. 11.8.
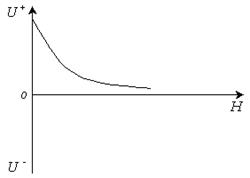
Рис. 11.8 Зависимость энергии отталкивания от расстояния между частицами.
Полная энергия взаимодействия между частицами получается путем сложения энергии притяжения в результате действия молекулярных сил и отталкивания в результате действия электрических сил.
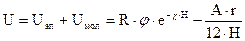 (11.8)
(11.8)
Результирующая потенциальная кривая взаимодействия частиц показана на рис.11.9.

Рис. 11.9 Результирующая кривая изменения энергии взаимодействия частиц в зависимости от расстояния между ними. 1-энергия отталкивания, 2-энергия притяжения, 3-полная энергия.
При 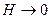
 ,
, 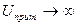 .
.
На результирующей потенциальной кривой имеется три области. В области малых 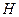 порядка 1 нм преобладают силы притяжения, так как при
порядка 1 нм преобладают силы притяжения, так как при 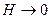
 ,
, 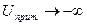 . Это выражается в существовании на результирующей кривой первичного минимума,
. Это выражается в существовании на результирующей кривой первичного минимума,  или ближней потенциальной ямы. Существование
или ближней потенциальной ямы. Существование  определяет необратимую агрегацию частиц. В области средних расстояний
определяет необратимую агрегацию частиц. В области средних расстояний 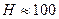
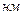 , равных толщине ионной оболочки, преобладают силы электростатического отталкивания. В этой области происходит перекрывание ДЭС соседних частиц, и силы отталкивания велики. Это определяет существование на результирующей кривой энергетического барьера
, равных толщине ионной оболочки, преобладают силы электростатического отталкивания. В этой области происходит перекрывание ДЭС соседних частиц, и силы отталкивания велики. Это определяет существование на результирующей кривой энергетического барьера 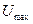 , величина которого определяет вероятность слипания частиц. Чем выше
, величина которого определяет вероятность слипания частиц. Чем выше 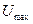 , тем меньше вероятность его преодоления, тем устойчивее система.
, тем меньше вероятность его преодоления, тем устойчивее система.
Энергия отталкивания является экспоненциальной функцией расстояния между частицами, а энергия притяжения – степенной функцией. Экспоненциальная зависимость 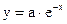 при больших значениях x убывает быстрее степенной
при больших значениях x убывает быстрее степенной  . Поэтому притяжение будет преобладать при больших расстояниях между частицами. В области больших расстояний
. Поэтому притяжение будет преобладать при больших расстояниях между частицами. В области больших расстояний 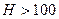
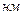 преобладают силы притяжения, т.к. они убывают по степенной функции медленнее, чем силы отталкивания. В результате этого на результирующей кривой появляется вторичный минимум,
преобладают силы притяжения, т.к. они убывают по степенной функции медленнее, чем силы отталкивания. В результате этого на результирующей кривой появляется вторичный минимум, 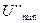 , или дальняя потенциальная яма.
, или дальняя потенциальная яма. 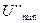 определяет обратимую агрегацию частиц, в том числе явление тиксотропии. Существование
определяет обратимую агрегацию частиц, в том числе явление тиксотропии. Существование 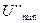 объясняет ряд других явлений. Так, малые частицы, прилипшие к стенке, совершают около нее интенсивное броуновское движение. В латексах можно наблюдать движение мелких частиц вокруг более крупных.
объясняет ряд других явлений. Так, малые частицы, прилипшие к стенке, совершают около нее интенсивное броуновское движение. В латексах можно наблюдать движение мелких частиц вокруг более крупных.
Результирующая потенциальная кривая взаимодействия частиц может быть представлена грубой механической моделью в виде шара, находящегося на рельефной поверхности (рис. 11.10).
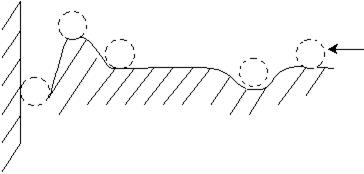
Рис. 11.10. Механическая модель взаимодействия частиц.
11.6.Коагуляция.
Различают коагуляцию явную, наблюдаемую невооруженным глазом, и скрытую, наблюдаемую при помощи приборов. Коагуляция может быть вызвана действием различных факторов: температуры, механических воздействий, введения электролитов и других веществ.
Агрегативная устойчивость резко изменяется при малых добавках электролитов. При критической концентрации наступает быстрая коагуляция. Значение критической концентрации, или порога коагуляции, резко уменьшается с ростом заряда противоионов в соответствии с правилом Шульца-Гарди: 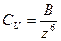 .
.
Дата добавления: 2020-11-18; просмотров: 993;











