Дискретная модуляция аналоговых сигналов

Дискретные способы модуляции основаны на дискретизации непрерывных процессов как по амплитуде, так и по времени (рис. 3). Рассмотрим принципы искретной модуляции на примереимпулъсно-кодовой модуляции, ИКМ (Pulse Amplitude Modulation, РАМ), которая широко применяется в цифровой телефонии.

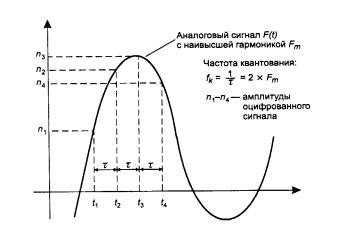
Рис. 3. Дискретная модуляция непрерывного процесса

Амплитуда исходной непрерывной функции измеряется с заданным периодом - за счет этого происходит дискретизация по времени. Затем каждый замер представляется в виде двоичного числа определенной разрядности, что означает дискретизацию по значениям функции - непрерывное множество возможных значений амплитуды заменяется дискретным множеством ее значений. Устройство, которое выполняет подобную функцию, называется аналого-цифровым преобразователем (АЦП). После этого замеры передаются по каналам связи в виде последовательности единиц и нуле� �. При этом применяются те же методы кодирования, что и в случае передачи изначально дискретной информации, то есть, например, методы, основанные на коде B8ZS или 2В 1Q.

На приемной стороне линии коды преобразуются в исходную последовательность бит, а специальная аппаратура, называемая цифро-аналоговым преобразователем (ЦАП), производит демодуляцию оцифрованных амплитуд непрерывного сигнала, восстанавливая исходную непрерывную функцию времени.

Дискретная модуляции основана на теории отображения Найквиста - Котельникова. В соответствии с этой теорией, аналоговая непрерывная функция, переданная в виде последовательности ее дискретных по времени значений, может быть точно восстановлена, если частота дискретизации была в два или более раз выше, чем частота самой высокой гармоники спектра исходной функции.

Если это условие не соблюдается, то восстановленная функция будет существенно отличаться от исходной.

Для качественной передачи голоса в методе ИКМ используется частота квантования амплитуды звуковых колебаний в 8000 Гц. Это связано с тем, что в аналоговой телефонии для передачи голоса был выбран диапазон от 300 до 3400 Гц, который достаточно качественно передает все основные гармоники собеседников. В соответствии с теоремой Найквиста - Котельникова для качественной передачи голоса достаточно выбрать частоту дискретизации, в два раза превышающую самую высокую гармонику непрерывного сигнала, то есть 2 * 3400 = 6800 Гц. Выбранная в действительности час тота дискретизации 8000 Гц обеспечивает н екоторый запас качества. В методе ИКМ обычно используется 7 или 8 бит кода для представления амплитуды одного замера. Соответственно это дает 127 или 256 градаций звукового сигнала, что оказывается вполне достаточным для качественной передачи голоса.

8) Протоколы сжатия данных

Как известно, применение сжатия данных позволяет более эффективно использовать емкость дисковой памяти. Не менее полезно применение сжатия при передачи информации в любых системах связи. В последнем случае появляется возможность передавать значительно меньшие (как правило, в несколько раз) объемы данных и, следовательно, требуются значительно меньшие ресурсы пропускной способности каналов для передачи той же самой информации. Выигрыш может выражаться в сокращении времени занятия канала и, соответственно, в значительной экономии арендной платы.

Научной предпосылкой возможности сжатия данных выступает известная из теории информации теорема кодирования для канала без помех, опубликованная в конце 40-х годов в статье Клода Шеннона "Математическая теория связи". Теорема утверждает, что в канале связи без помех можно так преобразовать последовательность символов источника (в нашем случае DTE) в последовательность символов кода, что средняя длина символов кода может быть сколь угодно близка к энтропии источника сообщений Н(Х), определяемой как:

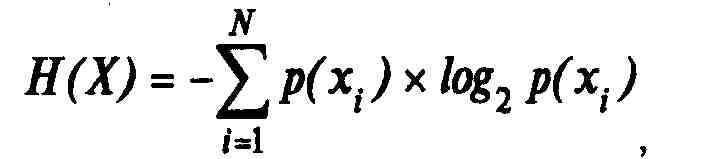
где p(xf) — вероятность появления конкретного сообщения .с, из N возможных символов алфавита источника. Число N называют объемом алфавита источника.

Энтропия источника Н(Х) выступает количественной мерой разнообразия выдаваемых источником сообщений и является его основной характеристикой. Чем выше разнообразие алфавита Х сообщений и порядка их появления, тем больше энтропия Н(Х) и тем сложнее эту последовательность сообщений сжать. Энтропия источника максимальна, если априорные вероятности сообщений и вероятности их выдачи являются равными между собой. С другой стороны,Н(Х)=0, если одно из сообщений выдается постоянно, а появление других сообщений невозможно.

Единицей измерения энтропии является бит. 1 бит — это та неопределенность, которую имеет источник с равновероятной выдачей двух возможных сообщений,' обычно символов "О" и "1".

Энтропия Н(Х) определяет среднее число двоичных знаков, необходимых для кодирования исходных символов (сообщений) источника. Так, если исходными символами являются русские буквы (N=32=2 ) и они передаются равновероятно и независимо, то Н(Х)=5 бит. Каждую буквы можно закодировать последовательностью из пяти двоичных символов, поскольку существуют 32 такие последовательности. Однако можно обойтись и меньшим числом символов на букву. Известно, что для русского литературного текста Я(Х)=1,5 бит, для стихов Н(Х)=\ ,0 бит, а для текстов телеграмм Н(.Х)=0,8 бит. Следовательно, возможен способ кодирования в котором в среднем на букву русского текста будет затрачено немногим более 1,5, 1,0 или даже 0,8 двоичных символов.

Если исходные символы передаются не равновероятно и не независимо, то энтропия источника будет ниже своей максимальной величины Я^^(Х)=/о<7^У. В этом случае возможно более экономное кодирование. При этом на каждый исходный символ в среднем будет затрачено и*= Н(Х) символов кода. Для характеристики достижимой степени сжатия используется коэффициент избыточности КИЗБ^^ —Н(Х)/Нмд^(Х). Для характеристики же достигнутой степени сжатия на практике применяют так называемый коэффициент сжатия Кеж- Коэффициент сжатия — это отношение первоначального размера данных к их размеру в сжатом виде, — обычно дается в формате К.сж'-^- Путем несложных рассуждений можно получить соотношение РИЗБ ^1—1 /^еж-Известные методы сжатия направлены на снижение избыточности, вызванной как неравной априорной вероятностью символов, так и зависимостью между порядком поступления символов. В первом случае для кодирования исходных символов используется неравномерный код. Часто появляющиеся символы кодируются более коротким кодом, а менее вероятные (редко встречающиеся) — более длинным кодом.

Устранение избыточности, обусловленной корреляцией между символами, основано на переходе от кодирования отдельных символов к кодированию групп этих символов. За счет этого происходит укрупнение алфавита источника, так как число N тоже растет. Общая избыточность при укрупнении алфавита не изменяется. Однако уменьшение избыточности, обусловленной взаимными связями символов, сопровождается соответствующим возрастанием избыточности, обусловленной неравномерностью появления различных групп символов, то есть символов нового укрупненного алфавита. Происходит как бы конвертация одного вида избыточности в другой.

Таким образом, процесс устранения избыточности источника сообщений сводится к двум операциям — декорреляции (укрупнению алфавита) и кодированию оптимальным неравномерным кодом.

Сжатие бывает с потерями и без потерь. Потери допустимы при сжатии (и восстановлении) некоторых специфических видов данных, таких как видео и аудиоинформация. По мере развития рынка видеопродукции и систем мультимедиа все большую популярность приобретает метод сжатия с потерями MPEG 2 (Motion Pictures Expert Group), обеспечивающий коэффициент сжатия до 20:1. Если восстановленные данные совпадают с данными, которые были до сжатия, то имеем дело со сжатием без потерь. Именно такого рода методы сжатия применяются при передаче информации в СПД.

На сегодняшний день существует множество различных алгоритмов сжатия данных без потерь, подразделяющихся на несколько основных групп.

Кодирование повторов {Run-Length Encoding, RLE).