В МЕТОДЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
В предыдущем параграфе матрица жесткости 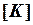 и вектор нагрузки
и вектор нагрузки 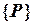 конечно-элементной модели конструкции формировались в предположении отсутствия опорных связей. Поэтому систему разрешающих уравнений
конечно-элементной модели конструкции формировались в предположении отсутствия опорных связей. Поэтому систему разрешающих уравнений
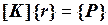 (4.7.1)
(4.7.1)
необходимо далее преобразовать так, чтобы перемещения 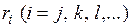 по направлениям опорных связей при решении преобразованной системы были равны нулю (в случае абсолютно жестких опор). Для этого можно использовать три способа.
по направлениям опорных связей при решении преобразованной системы были равны нулю (в случае абсолютно жестких опор). Для этого можно использовать три способа.
Первый способ заключается в удалении из системы (4.7.1) уравнений с номерами 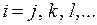 , соответствующими номерам нулевых перемещений по направлениям опорных связей, что, очевидно, приводит к уменьшению порядка полученной системы уравнений. Но в этом случае естественным образом изменятся номера оставшихся (ненулевых) узловых перемещений конструкции, что создаст проблему дальнейшей идентификации узловых перемещений конечных элементов, необходимых для определения их напряженного состояния, с использованием прежней матрицы индексов перемещений. Поэтому описанный способ учета условий закрепления конструкции имеет в методе конечных элементов весьма ограниченное применение.
, соответствующими номерам нулевых перемещений по направлениям опорных связей, что, очевидно, приводит к уменьшению порядка полученной системы уравнений. Но в этом случае естественным образом изменятся номера оставшихся (ненулевых) узловых перемещений конструкции, что создаст проблему дальнейшей идентификации узловых перемещений конечных элементов, необходимых для определения их напряженного состояния, с использованием прежней матрицы индексов перемещений. Поэтому описанный способ учета условий закрепления конструкции имеет в методе конечных элементов весьма ограниченное применение.
Второй способ заключается в обнулении строк и столбцов с номерами 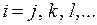 матрицы
матрицы 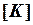 кроме диагональных элементов
кроме диагональных элементов 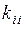 . В векторе
. В векторе 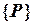 обнуляются соответствующие элементы
обнуляются соответствующие элементы 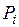 . В результате уравнения с номерами
. В результате уравнения с номерами 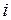 системы (4.7.1) будут иметь вид
системы (4.7.1) будут иметь вид 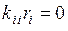 , откуда следует
, откуда следует 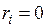 . Данный способ можно использовать и для учета кинематических воздействий (заданных перемещений
. Данный способ можно использовать и для учета кинематических воздействий (заданных перемещений 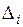 в направлениях опорных связей). В этом случае с матрицей
в направлениях опорных связей). В этом случае с матрицей 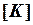 осуществляются прежние процедуры, а элементы
осуществляются прежние процедуры, а элементы 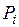 вектора
вектора 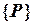 заменяются произведениями
заменяются произведениями 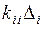 . В результате уравнения с номерами
. В результате уравнения с номерами 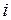 системы (4.7.1) будут такими:
системы (4.7.1) будут такими: 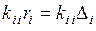 . Отсюда следует требуемое условие
. Отсюда следует требуемое условие 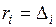 . Преимущество данного способа перед предыдущим состоит в возможности использования прежней матрицы индексов перемещений при дальнейшем определении узловых перемещений конечных элементов, входящих в состав вектора перемещений
. Преимущество данного способа перед предыдущим состоит в возможности использования прежней матрицы индексов перемещений при дальнейшем определении узловых перемещений конечных элементов, входящих в состав вектора перемещений 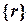 всей конструкции. Следует также отметить, что уравнения типа
всей конструкции. Следует также отметить, что уравнения типа 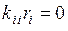 или
или 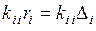 решаются не отдельно, а совместно со всеми уравнениями (4.7.1) с использованием какого-либо стандартного метода решения систем линейных алгебраических уравнений.
решаются не отдельно, а совместно со всеми уравнениями (4.7.1) с использованием какого-либо стандартного метода решения систем линейных алгебраических уравнений.
Третий способ состоит в умножении диагональных элементов 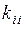 матрицы
матрицы 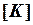 на параметр штрафа
на параметр штрафа 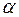 , выбираемый в диапазоне
, выбираемый в диапазоне 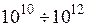 . В результате уравнения с номерами
. В результате уравнения с номерами 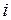 системы (4.7.1) будут такими:
системы (4.7.1) будут такими:
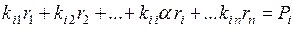 . (4.7.2)
. (4.7.2)
Слагаемое с параметром 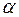 в уравнении (4.7.2) примерно в
в уравнении (4.7.2) примерно в 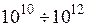 больше других слагаемых. Это приводит к тому, что перемещения
больше других слагаемых. Это приводит к тому, что перемещения 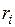 получаются практически равными нулю. При учете заданных перемещений
получаются практически равными нулю. При учете заданных перемещений 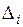 элементы
элементы 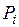 вектора
вектора 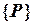 заменяются произведениями
заменяются произведениями 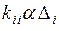 . Тогда вместо (4.7.2) будем иметь:
. Тогда вместо (4.7.2) будем иметь:
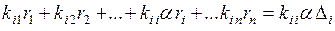 . (4.7.3)
. (4.7.3)
Это дает перемещения 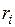 близкие к заданным перемещениям
близкие к заданным перемещениям 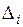 . Погрешность выполнения условий
. Погрешность выполнения условий 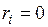 или
или 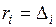 в данном способе имеет порядок
в данном способе имеет порядок 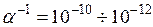 , что вполне пригодно для инженерных расчетов. Описанный способ учета условий закрепления конструкции имеет такое же преимущество, как и второй, состоящее в сохранении начальных номеров узловых перемещений конструкции. Его рекомендуется использовать в том случае, когда все ненулевые элементы матрицы
, что вполне пригодно для инженерных расчетов. Описанный способ учета условий закрепления конструкции имеет такое же преимущество, как и второй, состоящее в сохранении начальных номеров узловых перемещений конструкции. Его рекомендуется использовать в том случае, когда все ненулевые элементы матрицы 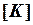 расположены вблизи ее главной диагонали, образуя достаточно узкую ленту. Тогда (с целью экономии необходимого объема оперативной памяти компьютера) матрицу
расположены вблизи ее главной диагонали, образуя достаточно узкую ленту. Тогда (с целью экономии необходимого объема оперативной памяти компьютера) матрицу 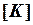 можно формировать не в квадратном, а прямоугольном массиве: первый столбец массива содержит главную диагональ данной матрицы; следующие столбцы – ненулевые диагонали, расположенные выше или ниже главной диагонали. Кроме того, указанная схема формирования матрицы
можно формировать не в квадратном, а прямоугольном массиве: первый столбец массива содержит главную диагональ данной матрицы; следующие столбцы – ненулевые диагонали, расположенные выше или ниже главной диагонали. Кроме того, указанная схема формирования матрицы 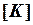 позволяет использовать специальные эффективные методы решения систем линейных алгебраических уравнений, ориентированные на симметрию и ленточную структуру матрицы
позволяет использовать специальные эффективные методы решения систем линейных алгебраических уравнений, ориентированные на симметрию и ленточную структуру матрицы 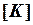 (метод разложения Холесского, метод
(метод разложения Холесского, метод 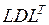 - факторизации, профильный метод).
- факторизации, профильный метод).
Дата добавления: 2016-07-27; просмотров: 1691;











