Частичные дислокации в кристаллах с различной структурой. Гранецентрированная кубическая структура

Как отмечалось выше, наиболее важной характеристикой дислокации является вектор Бюргерса, так как он определяет смещение атомов, происходящее при движении дислокаций в решетке. Величина вектора Бюргерса зависит от кристаллической структуры материала, потому что во время скольжения необходимо сохранять расположение атомов в решетке идентичным и механически стабильным как до, так и после прохождения дислокации.

Такое стабильное расположение атомов в решетке может быть достигнуто, если дислокация имеет вектор Бюргерса, в точности равный одному межатомному расстоянию (вектору решетки). Энергия дислокации пропорциональна квадрату вектора Бюргерса, поэтому такая полная, или совершенная дислокация имеет наименьшую энергию, когда ее вектор Бюргерса равен наименьшему возможному расстоянию между атомами в решетке.

Этот вектор, по определению, должен быть параллелен направлению плотнейшей упаковки атомов в структуре, что согласуется с результатами исследования направлений скольжения. Вектор Бюргерса определяется его составляющими по трем главным осям кристалла.

В гранецентрированной кубической структуре наименьший вектор решетки соединяет вершину куба в элементарной ячейке с центром ближайшей грани; (а/2, а/2, 0) — компоненты этого вектора, α₁₁₀/2 —его кристаллографическое обозначение. Величина такого вектора составляет

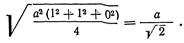
Для объемноцентрированной кубической структуры наименьший вектор решетки, как легко видеть, составляет b = α₁₁₁/2, а для гексагональной плотноупакованной структуры b = α₁₁₂₀

В ряде процессов, происходящих при пластической деформации кристалла, вектор Бюргерса дислокации может не быть равным этому вектору решетки; такие дислокации называются частичными. Примером деформации, в которой участвуют частичные дислокации, может служить двойникование.

Напомним кратко различия между скольжением и двойникованием. При скольжении верхняя половина кристалла движется относительно нижней вдоль определенной кристаллографической плоскости (плоскости скольжения) и атомы перемещаются на целое число межатомных расстояний; в результате сохраняется непрерывность кристаллической решетки.

При двойниковании перемещения атомов не равны целым межатомным расстояниям и решетка в верхней области является как бы зеркальным изображением решетки в нижней области. Плоскость, разделяющая эти области, носит название плоскости двойникования. В отличие от скольжения при двойниковании область, в которой произошел сдвиг атомов из равновесных положений, занимает много атомных плоскостей, причем атомы в каждой плоскости последовательно сдвинуты на одно и то же расстояние по отношению к атомам предыдущей плоскости.

Частичные дислокации также могут играть важную роль и при скольжении, если условия деформации таковы, что паре частичных дислокаций, каждая из которых связана с меньшим искажением решетки, перемещаться легче, чем полной дислокации. Такая пара частичных дислокаций носит название вытянутой дислокации.

Решетка, остающаяся после прохождения первой частичной дислокации, не идентична исходной решетке, и возникает нарушение структуры, носящее название дефекта упаковки. После прохождения второй частичной дислокации правильность строения решетки восстанавливается.

Гранецентрированная кубическая структура. Рассмотрим более подробно частичные дислокации в плотноупакованных кристаллах [21]. Выше указывалось, что обе плотноупакованные структуры — гранецентрированная кубическая и гексагональная — могут быть построены путем наложения плоскостей, состоящих из плотноупакованных сфер. Рассмотрим расположение атомов в плотноупакованных слоях гранецентрированной кубической структуры.

На рис. 3.11, а показан слой атомов А; следующие слои занимают положения В и С. Индексы 'всех этих слоев (111). Вектор b₁ на рисунке соответствует вектору Бюргерса полной дислокации и дает перемещение в плоскости В. Однако возможен и другой путь перемещения атомов, а именно, атом, находящийся в плоскости В, может перейти в ближайшее положение в плоскости С (вектор b₂ на рисунке), а затем опять в плоскость В (вектор b₃ на рисунке).

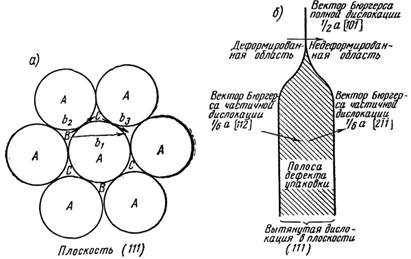
Рис. 3.11. а) проекция гранецентрированной кубической структуры на плоскость (111), б) взаимное расположение частичных дислокаций и дефекты упаковки в гранецентрированной кубической структуре

Таким образом, вектор b₁ (кристаллографическое обозначение α₁₀₁/2) дает такое же смещение, как сумма векторов b₂ = α₂₁₁/6 и b₃ = α₁₁₂/6, причем в последнем случае атомы совершают зигзагообразный путь: из плоскости В в плоскость С и затем опять в плоскость В.

На первом этапе этого процесса атомы переходят из положений В в положения С, при этом в слоях (111) возникают дефекты упаковки и последовательность атомов изменяется от АВСАВС к АВСАСАВС, т. е. для некоторой части слоев трехслойная упаковка {АВСАВС) заменяется двухслойной (АСАС). Во время второй части процесса скольжения правильная последовательность слоев восстанавливается. Таким образом, единичная полная дислокация при скольжении диссоциирует по реакции

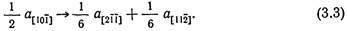
Такой процесс диссоциации казалось бы энергетически выгоден, так как сумма квадратов векторов Бюргерса частичных дислокаций меньше, чем квадрат вектора Бюргерса полной дислокации. Соответственно в квадратах вектора Бюргерса (без учета направлений) реакцию можно записать так:

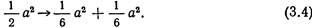
Эти полудислокации, или так называемые частичные дислокации Шокли, отталкивают друг друга с силой, приближенно равной 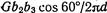, где G — модуль сдвига, d — расстояние между частичными дислокациями.

Взаимное расположение частичных дислокаций и дефекта упаковки показано на рис. 3.11,6. Полоса дефекта упаковки образуется в плоскости скольжения между частичными дислокациями. Вследствие образования дефекта упаковки, имеющего большую энергию, чем нормальная решетка, частичные дислокации не могут разойтись очень далеко.

Если γ — энергия на единицу площади дефекта упаковки, то сила на единицу длины, действующая на дислокацию со стороны дефекта упаковки, также равна γ и для нахождения равновесного расстояния d следует приравнять силу отталкивания Ga²/24πd между двумя частичными дислокациями силе γ, действующей на дефект. Отсюда равновесное расстояние между двумя частичными дислокациями будет равно

Из этого соотношения видно, что ширина полосы дефекта упаковки обратно пропорциональна энергии этого дефекта упаковки. Таким образом, для того чтобы ответить на вопрос, будет ли происходить диссоциация полной дислокации на частичные, недостаточно найти соотношение между их энергиями (квадратами векторов Бюргерса), а необходимо учесть также и энергию дефектов упаковки.

Прямые измерения энергии дефектов упаковки можно проводить электронномикроскопическим методом. Кроме того, существует несколько косвенных методов оценки этой величины. Малая величина энергии дефектов упаковки характерна для таких металлов, как медь, серебро, золото; большая величина — для алюминия, свинца, магния.

Это различие связано со следующими обстоятельствами. Во всех металлах образование дефектов упаковки в плотноупакованных плоскостях влияет на границу зоны Бриллюэна, так как эта граница связана с наиболее плотноупакованными плоскостями. Однако энергия при образовании дефектов упаковки сильно повышается только в тех металлах, в которых поверхность Ферми близка к границе зоны Бриллюэна.

Эту классификацию подтверждают результаты опытов по измерению частоты появления двойников отжига, в которых дефект упаковки может рассматриваться как тонкий двойник. Так, например, в алюминии — материале с высоким значением энергии дефектов упаковки — двойники отжига встречаются очень редко, а в меди, имеющей малую энергию дефектов упаковки, обычно содержится много двойников.

Из анализа изменений энергетических состояний электронов следует, что при образовании сплавов может понижаться энергия дефектов упаковки и, например, двойники отжига в сплаве медь-цинк (а-латунь) должны встречаться чаще, чем в чистой меди. Энергия границы двойника составляет, по-видимому, половину энергии дефекта упаковки, так что оценить величину у можно с помощью исследований двойников.. Оценка у по исследованиям двойников дает величины около 40 эрг/см² для меди и около 200 эрг/см² для алюминия.