Кристаллы, состоящие из атомов одного сорта

Дислокации в простой кубической структуре. Вообще говоря, в решетке можно выделить любое число семейств плоскостей с различными межатомными расстояниями, но как будет показано ниже, из энергетических соображений следует, что в кристаллах реально существуют дислокации с минимальными векторами Бюргерса. Очевидно, что минимальным межатомным расстоянием в простой кубической структуре являются α₁₀₀

Реальных винтовых дислокаций в структуре, очевидно, может быть столько же, сколько различных направлений вектора Бюргерса. Линия дислокации -совпадает с вектором Бюргерса, расположенным вдоль <100>. Следовательно, возможны шесть различных вариантов или, с точностью до знака, три. Для краевых дислокаций с вектором Бюргерса α₁₀₀ число направлении линий дислокации неограниченно.

Действительно, условие перпендикулярности вектора Бюргерса и линии дислокации удовлетворяется, если линия дислокации идет в произвольном направлении в плоскости, перпендикулярной вектору Бюргерса. Рассмотрим дислокацию с вектором Бюргерса, лежащим в направлении [110].

Если создавать такую дислокацию путем удаления части плоскости (100) и смещения сторон разреза в перпендикулярном направлении (т. е. так, как это делалось для дислокации с b = α₁₀₀), то нельзя получить физически реальную конфигурацию атомов.

Действительно, как видно из рис. 3.4, атомы в последовательных плоскостях (110) находятся в чередующихся положениях и удаление одной из плоскостей с последующим смещением в перпендикулярном направлении привело бы к нестабильному расположению атомов. Другими словами, вектор [а/₂, а/₂, 0], перпендикулярный плоскости (110), не является вектором решетки в простой кубической системе.

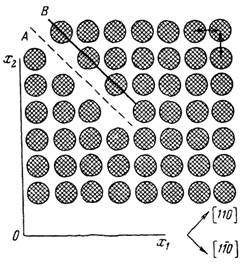
Рис. 3.4. Схема, иллюстрирующая трудность образования дислокации с вектором Бюргерса α₁₀₀ в простой кубической решетке

Получить полную дислокацию можно, если после удаления плоскости (110) на рис. 3.4 осуществить смещение одновременно в перпендикулярном направлении на [а/2, а/2, 0] и в тангенциальном направлении на [а/2, а/2,0]. Таким образом, суммарное смещение составляет [а, 0, 0], и в результате возникает полная единичная дислокация.

Другим путем создания дислокаций является удаление не одного, а двух атомных слоев (А и В на рис. 3.4). В этом случае можно получить дислокацию путем нормального перемещения поверхностей разреза на величину а √2. Возникающая дислокация имеет вектор Бюргерса α₁₀₀, являющийся вектором решетки.

Из рассмотрения возможных направлений векторов Бюргерса можно видеть, что

Написанное соотношение называется дислокационной реакцией, которая идет в направлении выигрыша энергии, т. е. в направлениях диссоциации (расщепления) или объединения дислокаций.

Приведенные выше рассуждения относятся к краевой дислокации; винтовая дислокация с линией дислокации, параллельной [110], может образоваться также с вектором Бюргерса α₁₀₀ с модулем а √2 и также может расщепляться на две единичных дислокации. Схема расположения атомов при этом имеет более сложный характер; если проводить разрез в плоскости (111), то схема еще более усложняется. Поэтому ниже будем рассматривать не все возможные типы дислокации, а только те, роль которых в пластической деформации достаточно хорошо изучена.

Дислокации в гранецентрированной кубической структуре. В гранецентрированной кубической структуре наименьшими векторами решетки являются векторы типа [а/2, а/2, 0]; следовательно, наиболее вероятным является существование дислокаций с этими векторами в качестве векторов Бюргерса [19]. Такие векторы (как лежащие в плоскостях {111} и направлениях <110>) можно описать в кристаллографических символах.

Рассмотрим расположение атомов в элементарной ячейке гранецентрированного куба. На рис. 3.5, а показаны две соседние элементарные ячейки, в одной из которых выделены атомы, входящие в плоскость октаэдра (111) (QPR на рисунке), а также выделены атом В в вершине ячейки (т. е. из следующей плоскости типа (111)—плоскости В) и атом С из расположенной рядом ячейки (также в плоскости типа (111) — плоскости С); расстояния ВС = FB = ½ а √2.

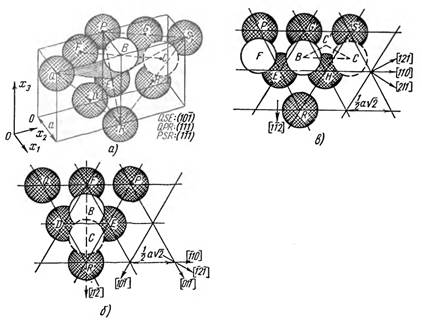
Рис. 3.5. Расположение атомов в плоскостях {111} гранецентрированной кубической решетки: а) объемная модель двух элементарных ячеек, б) проекция модели на плоскость (111), в) проекция на плоскость (111)

На рис. 3.5, 6 показана проекция структуры на плоскость (111). На рисунке нанесены основные кристаллографические направления, показана первая плоскость (111) и даны по одному атому из двух последующих. Положения атомов (если обозначить положения всех атомов первого слоя Q, F, Р и т. д. буквой А) могут быть представлены последовательностью АВСАВС... Стороны треугольных ячеек равны а√2/2, расстояния между последовательными плоскостями (111), измеренные в направлении, перпендикулярном к этим плоскостям, равны а√3/3.