Объемноцентрированная кубическая структура

В объемноцентрированной кубической структуре наименьший вектор решетки равен α₁₁₁/2. Этот вектор соединяет атомы в вершине и центре куба, а его направление совпадает с наблюдаемым направлением скольжения. Дислокация в плоскости (211) с ректорами Бюргерса α₁₁₁/2 может, в принципе, понизить энергию путем дислокации по следующей реакции:

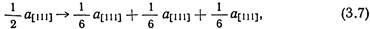
но дефект упаковки, возникающий при этом между первой и -второй частичными дислокациями, отличается от дефекта упаковки между второй и третьей частичными дислокациями. Один из этих дефектов упаковки соответствует расположению атомов, не наблюдаемому в объемноцентрированной кубической структуре, а другой соответствует двойникующему сдвигу.

Поэтому обычно предполагают, что энергия дефекта упаковки второго типа слишком высока для того, чтобы происходила заметная диссоциация. Аналогичная ситуация рассматривалась выше для алюминия, имеющего гранецентрированную кубическую структуру и очень высокую энергию дефектов упаковки.

Эффективная диссоциация полных дислокаций может проходить по реакции:

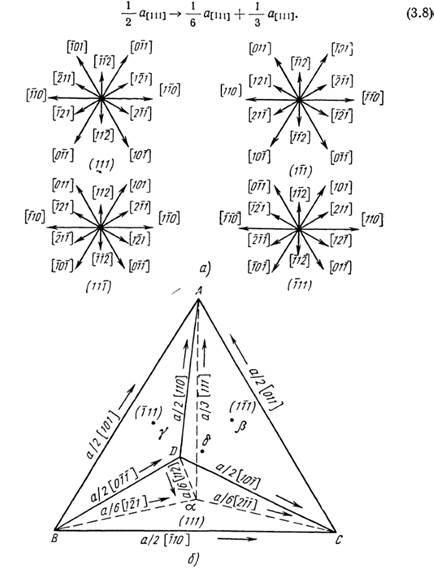
Рис. 3.14. Построения, облегчающие анализ дислокационных реакций в кристаллах с гранецентрированной кубической структурой: а) направления скольжения в четырех плоскостях семейства {111}, б) тетраэдр Томпсона

Эта реакция диссоциации напоминает рассмотренную выше реакцию для гранецентрированной кубической структуры, но в этом случае частичные дислокации имеют параллельные векторы Бюргерса, обе они относятся к винтовому типу, если линии дислокаций лежат вдоль [111]. Однако линия [111] является линией пересечения трех плоскостей типа {211}, наклоненных по отношению друг к другу на 120°. Винтовая дислокация в объемноцентрированной кубической структуре может диссоциировать во всех трех плоскостях и образовывать дефекты упаковки двойникового типа по реакции

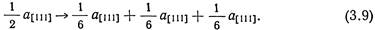
Дислокация полных дислокаций с возникновением дефектов упаковки двойникового типа имеет большое значение для объяснения механического двойникования; она играет также важную роль в упрочнении материалов с объемноцентрированной кубической структурой и в изменении механических свойств при изменении температуры.

Рассмотрим подробнее возможные атомные модели дефектов упаковки в материалах с объемноцентрированной кубической структурой [150]. В принимаемой обычно модели двойникования в объемноцентрированной кубической структуре когерентные границы двойников лежат в плоскостях, параллельных плоскости двойникования (112). Эти границы представляют собой плоскости, вдоль которых порядок расположения атомов меняется на обратный. Эти границы, таким образом, могут рассматриваться как имеющие энергию, эквивалентную половине энергии дефекта упаковки α₁₁₁/6, лежащего в той же плоскости, так как такой дефект упаковки эквивалентен однослойному двойнику.

Механические двойники в объемноцентрированной кубической структуре отличаются большой стабильностью, поэтому можно заключить, что энергия когерентной границы, равная энергии дефекта упаковки с плоскости типа {112}, невелика. В действительности, однако, дефекты упаковки рассмотренного типа, как правило, не наблюдаются, а наблюдаются двойники отжига и дефекты упаковки в других плоскостях.

Из этих наблюдений следует, что энергия дефекта упаковки в плоскости {112} должна быть велика и в других плоскостях должны существовать дефекты упаковки со сравнимой величиной энергии. Наблюдения показывают, что часто возникают границы в плоскостях {110}; следовательно, дефекты упаковки со сравнимой величиной энергии могут существовать и в других плоскостях. Из наблюдений формы механических двойников в металлах также следует, что границы часто возникают преимущественно в плоскостях {100}. Следовательно, энергетически выгодными являются дефекты упаковки типа α₁₁₁/6 в плоскостях {100}.

Для сравнительной оценки энергий рассмотрим смещения атомов в результате возникновения дефектов упаковки в плоскостях {112} и {110}. Введение дефекта упаковки в любую из атомных плоскостей (121) или (110) приводит к уменьшению минимального межатомного расстояния вдоль плоскости дефекта упаковки от

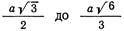
(от 0,866 а до 0,816 а). Отметим, однако, что расстояние между этими смещенными атомами в плоскости (111) неодинаково для разных типов дефектов упаковки, а именно: для дефектов упаковки в плоскости (112) она составляет а√2 а для плоскости {110} За I 6.

Если предположить, что энергия дефектов упаковки пропорциональна смещениям атомов, то окажется, что для дефектов упаковки в плоскости {112} она в 2√3 (=1,153) раза больше, чем для дефектов в плоскости {110}. Кроме того, деформации сжатия, возникающие вследствие смещений атомов, нормальны к плоскостям {112} и направлены под углом 30° к плоскостям {110}.

Во всяком случае очевидно, что оба вида дефектов упаковки требуют для своего образования значительной энергии, так как необходимое сжатие в плоскости дефекта составляет около 6% и при этом появление дефектов в плоскостях {110} не менее вероятно, чем в плоскостях {112}.

Другим механизмом, при помощи которого могут образовываться дефекты упаковки, является диссоциация винтовых дислокаций с вектором Бюргерса α₁₁₁/2. Можно построить схему расщепления дислокации в плоскости (112) с направлением линии дислокации < 111 > и вектором Бюргерса α₁₁₁/2 на три симметрично расположенные частичные дислокации в той же плоскости {112} и векторами Бюргерса α₁₁₁/6.

Для того чтобы произошла такая диссоциация, необходимо возникновение смещений трех соседних атомов в узле. Стабильная конфигурация при этом должна иметь плоскость симметрии в одной из частичных дислокаций, идущей вдоль линии пересечения плоскостей {112}. При диссоциации винтовой дислокации с тем же вектором Бюргерса α₁₁₁/2, но лежащей в плоскости (110), на три частичные дислокации с векторами Бюргерса α₁₁₁/6 смещения атомов несколько меньше, и, следовательно, такая конфигурация является более выгодной.

Рассмотрим возможность образования частичных дислокаций в плоскостях {110} материалов с объемноцентрированной кубической структурой. Диссоциация полных дислокаций на частичные в этом случае энергетически выгодна и частичные дислокации могут расходиться в материалах с малой энергией дефектов упаковки.

Рассмотрим расположение в плоскости (011) атомов материалов с объемноцентрированной кубической структурой. Во время скольжения, полной дислокации вдоль направления [111] действительный путь атомов может проходить через отрезки, направленные вдоль [011] и [211]. При этом движении атомы должны преодолеть «седловые точки», в которых меняется направление их движения. Реакция диссоциации в этом случае имеет вид

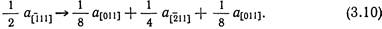
Если использовать модель жестких шаров, то для равновесия в правую часть уравнения нужно добавить малые члены α₀₁₁/50 и α₀₁₁/50 к первой и третьей частичным дислокациям. Эти члены описывают малые составляющие вектора Бюргерса в направлении, нормальном плоскости скольжения.

С помощью правила о том, что энергия дислокации пропорциональна квадрату вектора Бюргерса, можно подсчитать, что сумма энергий, приходящаяся на единицу длины для трех дислокаций в правой части уравнения, составляет 7/12 от энергии дислокации, стоящей в левой части, уравнения. При этом изменение ориентировок векторов Бюргерса при диссоциации также действует в направлении, благоприятном для диссоциации краевой дислокации.

Приведенная реакция в случае, когда все три возникающие частичные дислокации имеют винтовую ориентировку, дает неподвижное (сидячее) расположение дислокаций. Возникновение частичной дислокации, по-видимому, возможно только в тех случаях,, когда энергия дефектов упаковки мала.