Кристаллы, состоящие из разнородных атомов

В тех случаях, когда кристаллы состоят из разнородных атомов, структура дислокаций, как правило, усложняется. Рассмотрим структуры дислокаций в некоторых соединениях.

Дислокации в ионных кристаллах — структуре хлористого натрия. Как было отмечено выше, структура NaCl состоит из двух вставленных одна в другую гранецентрированных решеток, одна из которых состоит из ионов Na+, другая из ионов С1^-, а решетки смещены одна относительно другой на вектор с компонентами [а/2, а/2, а/2].

На рис. 3.10, а приведено расположение атомов в плоскости (001) кристалла NaCl. Из рисунка видно, что создать краевую дислокацию в NaCl так же, как в простой кубической структуре, не удается, так как если удалим часть плоскости (010), то, сдвинув края разреза, получим расположенные рядом одноименно заряженные ионы, что (по энергетическим соображениям) маловероятно.

Для создания дислокации необходимо удаление двух атомных слоев разноименных ионов, как показано на рис. 3.10, а. Дислокация, изображенная на рис. 3.10, а является краевой с вектором Бюргерса [а/2, а/2, 0] и линией дислокации, идущей вдоль [001], т. е. перпендикулярно плоскости чертежа. Дополнительным условием, которое необходимо выполнить при создании дислокации, является сохранение электрической нейтральности кристалла. Легко видеть, что для дислокации, изображенной на рис. 3.10, а, это условие выполняется. Следует также обратить ^внимание на то, что ряды ионов различного знака кончаются на разной высоте над условной линией дислокации.

Винтовая дислокация, изображенная на рис. 3.10, 6, также имеет линию дислокации, соединяющую ионы одного знака (А), и линию, соединяющую ионы другого знака (В). Вектор Бюргерса дислокации, изображенной на рисунке, равен [а/2, а/2, 0]; линия дислокации идет вдоль [110], т. е. по диагонали рисунка.

Дислокации в кристаллах со структурой сфалерита. Для более подробного анализа Дислокаций в материалах со структурой сфалерита, к которой, в частности, относятся полупроводниковые соединения типа A^IIIB^v, рассмотрим объемную модель этой структуры, расположенную таким образом, чтобы направление [111] было вертикальным (рис. 3.10, д) [119]. На этой модели структуры идеального кристалла показаны положение плоскости скольжения {111}, направления вектора Бюргерса b и линии дислокации а для так называемой 60°-ной дислокации (а=а₁₁₀, b = a₁₀₁, угол между векторами а и b составляет 60°).

При образовании дислокации атомы, расположенные выше плоскости скольжения, смещаются вправо на величину вектора Бюргерса α101/2. После этого, соединяя ближайшие атомы, лежащие по обе стороны от плоскости скольжения таким образом, чтобы удовлетворялись принципы простейшей ковалентной связи между атомами, получаем расположение атомов вокруг линии 60°-ной дислокации.

Следует отметить, что все атомы с разорванными связями в модели 60°-ной дислокации относятся к одному типу (черные кружки на рисунке). Таким образом, можно сказать, что (например, в соединении InSb) возможны Два типа 60°-ной дислокации. К одному из этих типов (а-дислокации) относятся такие дислокации, в которых все оборванные связи принадлежат атомам индия, т. е. лишняя полуплоскость кончается рядом атомов индия; к другому типу относятся те дислокации (ß-дислокации), в которых лишняя полуплоскость кончается рядом атомов сурьмы. Все сказанное относится также к соединениям элементов II и VI групп, I и VII групп периодической системы, также имеющим структуру сфалерита.

Из-за сходства структур алмаза и сфалерита большинство типов дислокаций, существующих в элементах со структурой алмаза, может наблюдаться также и в соединениях со структурой сфалерита. Примером может служить краевая дислокация с плоскостью скольжения {111}, направлением линии дислокации <112> и направлением вектора Бюргерса <110> (эти направления составляют угол 90°), а также 30°-я дислокация, отличающаяся от краевой дислокации только тем, что угол между линией дислокации и вектором Бюргерса составляет 30°.

Как видно из атомных схем дислокации, в этих случаях также возможны а- и ß-дислокации. Однако эта закономерность не является общей. Примером случая, когда она не имеет места, может служить приведенная на рис. 3.10, е атомная модель винтовой дислокации в структуре сфалерита. В этом случае как вектор Бюргерса, так и линия дислокации имеют направление <110>. Если их направления параллельны, то дислокация соответствует винтовой линии правого вращения, если направления антипараллельны—винтовой линии левого вращения.

Из анализа контура Бюргерса, приведенного на рисунке, видно, что в контуре 1—2—3—4—5—6 только один шаг, а именно 3—4, имеет компоненту, антипараллельную вектору Бюргерса. Этот шаг может быть пройден либо в последовательности черный кружок — белый кружок (как изображено на рисунке), либо в последовательности белый кружок черный кружок.

Следовательно, для винтовой дислокации правого вращения в структуре сфалерита возможны два типа расположения атомов, аналогично а- и ß-видам для дислокаций краевого типа либо для дислокаций, имеющих краевую компоненту. Те же рассуждения можно повторить и для винтовой дислокации левого вращения, т. е. в кристаллах со структурой сфалерита возможны 4 типа винтовых дислокаций.

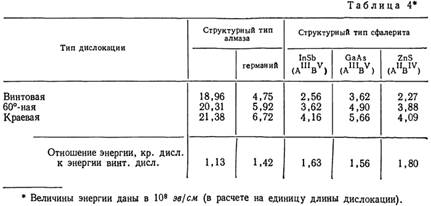
В заключение приведем соотношения между энергиями различных типов дислокаций в материалах со структурами алмаза и сфалерита (см. табл. 4). Таким образом, во всех случаях наиболее энергетически выгодным является образование винтовых дислокаций.

Дислокации в кристаллах со структурой карбида кремния. Кристаллы карбида кремния имеют слоистую гексагональную структуру, подробно рассмотренную в работах [1] и [18]. Приведем анализ типов дислокации [71] как возможных, так и обнаруженных экспериментально для одного из типов карбида кремния: SiC—6Н.

Если построить модель структуры из шаров, то можно проследить расположение плоскости скольжения для краевой дислокации. Из анализа модели следует, что плоскость скольжения в действительности не является плоскостью, а представляет собой поверхность с искривлениями, параллельными вектору скольжения.

Если прибегнуть к аналогии с кубической системой, то можно сказать, что:
- плоскость скольжения состоит из чередующихся полосок плоскостей (111) и (100);
- каждая полоска имеет ширину в три атомных слоя и лежит вдоль (111) или почти параллельно плоскости (100);

- индексы этих плоскостей в гексагональной структуре карбида кремния соответственно (1101) и (4401);
- результирующая волнистая поверхность лежит параллельно плоскости (3301);
- вектор Бюргерса параллелен плоскости (0001) и лежит в направлении [1120].

В структуре SiC—6Н единственными неволнистыми плоскостями являются плоскости, параллельные кристаллографической оси с. Это подтверждается наблюдениями над кристаллографией и формами полос скольжения и .спиралей роста на поверхности кристаллов.

Таким образом, дислокации в структуре карбида кремния могут иметь по меньшей мере два типа векторов Бюргерса, лежащих в плоскости базиса и имеющих компоненту, перпендикулярную кристаллографической оси с. Дислокации, имеющие вектор Бюргерса b = α₁₁₂₀. лежащий в плоскости базиса, обнаружены методами рентгеновской микроскопии и путем микроскопического анализа после скольжения.

Из всех возможных типов дислокаций с этим вектором Бюргерса большая часть, по-видимому, имеет чисто краевую ориентировку, хотя иногда наблюдаются и дислокации, линии которых составляют 30° и 60° с вектором Бюргерса, а также чисто винтовые дислокации. Наблюдаются также искривленные линии дислокации.

Экспериментально обнаружены дислокации, пересекающие плоскости базиса, с векторами Бюргерса, лежащими в плоскости базиса (b = α₁₁₂₀). Плоскость скольжения таких дислокаций — искривленная плоскость (3301), т. е. рассмотренная выше волнистая псевдоплоскость, составленная из полос плоскостей (1101) и (4401).

В связи с полярным типом межатомных связей в структуре карбида кремния в нем возможны два типа дислокаций. Рассмотрим уже упоминавшуюся выше модель пространственного расположения атомов в SiC.

В проведенном по плотно упакованному слою сечении идеальной структуры, не содержащей дислокаций, можно показать след плоскости (0001), перпендикулярной кристаллографической оси с. Можно построить две атомные модели краевых дислокаций противоположного знака, возможных в структуре карбида кремния (в первом случае дополнительная полуплоскость кончается рядом атомов кремния, во втором случае — рядом атомов углерода).

Кроме рассмотренных типов дислокаций в кристаллах карбида кремния возможны также дислокации с вектором Бюргерса, наклонным к кристаллографической оси с. Известно, что компонента вектора Бюргерса в направлении оси с для таких дислокаций, равная высоте ступеньки в элементарных спиралях роста на поверхности кристаллов, составляет 1/3 периода повторяемости вдоль оси с для кристаллов с ромбоэдрической структурой и с/2 или с для кристаллов с гексагональной структурой.