Основні поняття теорії графів
Теорія графів
Виникнення теорії графів пов’язують з іменем Леонарда Ейлера, який у 1736 р., коли працював в Російський Академії наук, не тільки розв’язав популярну на той час головоломку про кенігсбергські мости, а й знайшов критерій існування в графі спеціального маршруту (ейлерового циклу). Це задача про те чи можливо здійснити прогулянку таким чином, що якщо вийти з будь-якого місця міста повернутися в нього, проходячи один раз по кожному мосту? Місто Кенігсберг (Калінінград) розташовано на чотирьох частинах суші a, b, c, d тому їх було представлено у вигляді вершин, а сім мостів зображені ребрами, які з’єднують відповідні вершини. В результаті отримали граф (рис.1). Ейлер довів, що подібний маршрут має бути тільки для графа у якого кожна вершина зв’язана парним числом ребер .
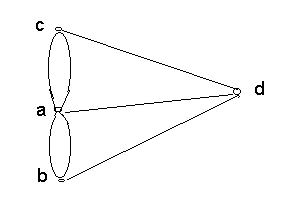
Рис. 1.
Теорія графів має потужний апарат рішення прикладних задач у самих різних сфер науки. До яких відносяться, наприклад теорія зв’язку, аналіз систем, проектування обчислювальних машин, архітектура, дослідження операцій, генетика, психологія, соціологія, економіка і т.д. Теорія графів також тісно пов’язана з такими розділами математики, як теорія множин, теорія матриць, математична логіка та теорія ймовірності. В усіх цих розділах графи застосовуються для представлення різних об’єктів.
В останні роки з’явилися дослідження, що показують особливе значення графів у сучасному суспільстві. Будь-який ринок (інформаційний) - це графова система зі своїми структурними елементами у вигляді покупців, продавців, пунктів продажу.
Час, у якому ми живемо, часто називають століттям глобалізації чи інформаційним століттям, підкреслюючи якісно нове значення інформації в ньому. Якісно нову роль отримали в новому часі і багато організаційних структур, переважну більшість яких організовано за принципом графів. Будь-які комунікаційні системи, організовані за принципом графів.
Основні поняття теорії графів
Граф - це форма задання відношень. Граф - графічна структура, яка складається з множини елементів, що називається вершинами і множини відношень між цими елементами, які позначаються в цій структурі лініями, що називаються ребрами або дугами.
Граф позначається буквою G, множина вершин V, множина відношень (дуг або ребер) – E, упорядкована пара G = (V, E). Нехай V = {v1, v2, ..., vn} і E = {e1, e2...,em}
При цьому елементи множини V зображають крапками на площині, а ребра (vi, vj ) — відрізками (прямолінійними або криволінійними), які з'єднують крапки vi та vj. Граф називається скінченним, якщо множини його вершин і ребер є скінченними. Кількість вершин графа n, а кількість ребер m. Граф, який містить n вершин та m ребер називають (n, m) - графом.
Кількість вершин n(G) графа називають його порядком.
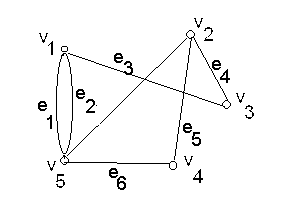
Рис. 2.
Граф, який є моделлю симетричного відношення називається простим або симетричним графом, неорієнтованим графом.
Граф G = (V, E), V = {v1, v2, v3 v4,, v5} і E = {e1, e2, e3, e4, e5, e6}. Ребра можуть задаватися ще послідовністю вершин E = {(v1, v5), (v1, v5), (v1, v3), (v2,,v3),(v2,v4), (v2, v5), (v4, v5)}.
Граф, який показує наявність декількох відношень між однією і тією ж множиною елементів називається мультиграфом.
Основна ознака мультиграфа – між деякими його вершинами існує декілька ребер або дуг.
Граф, який є моделлю несиметричного відношення називається орієнтованим графом. Щоб змоделювати несиметричне відношення треба вказати направлення ребер. Направлення показують стрілочкою. Стрілочка, яка відображає несиметричне відношення називається дугою графа.
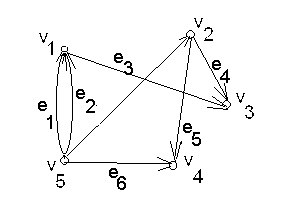
Рис. 3.
Таким чином для простого графа – граф складається з двох множин (вершин та ребер), для несиметричного графа – граф складається з двох множин (вершин та дуг).
Два ребра називаються суміжними, якщо обидва вони є інцидентними одній вершині.
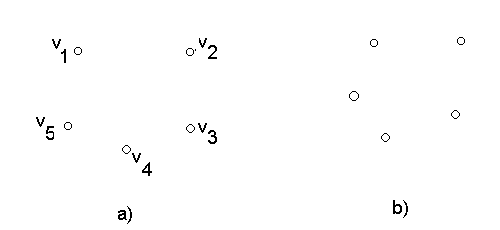
Рис. 4.
Якщо граф G = (V, Æ ) - множина відношень порожня (рис. 4, а).
Але якщо множина вершин V - порожня, то порожньою є також множина Е. Такий граф називається порожнім. Такий граф називається нуль-графом і позначається Æ (рис. 4, b).
Лінії, що зображають ребра графа, можуть перетинатися, але точки перетину не є вершинами; різні ребра можуть бути інцидентними одній і тій самій парі вершин (рис.2), такі ребра називаються кратними. Цей випадок відповідає наявності кількох однакових пар E = {(v1, v5), (v1, v5). Граф, що містить кратні ребра, називається мультиграфом.
Ребро може з'єднувати деяку вершину саму з собою (рис. 5), таке ребро називається петлею. Цей випадок відповідає наявності в множині Е пар вигляду (v, v). Граф із петлями та кратними ребрами називається псевдографом.
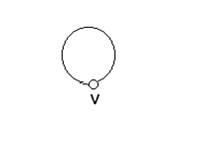
Рис. 5
Графи, які найчастіше розглядаються, є скінченними, тобто скінченні множини їхніх елементів (вершин і ребер), їх і розглядатимемо. Проте деякі поняття та результати, про які йтиметься, належать до довільних графів. Скінченний неорієнтований граф без петель і кратних ребер називається звичайним..
При зображенні орієнтованих графів напрямки ребер позначаються стрілками (рис. 3). Орієнтований граф може мати кратні ребра, петлі, а також петлі, що з'єднують ті ж самі вершини ребра, але у зворотних напрямках.
Є специфічний вид ребра або дуги, які і в симетричному і в орієнтованому називається однаково петля - модель рефлексивного відношення
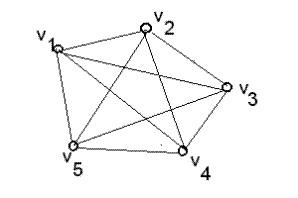
Рис. 6.
Повний граф G = (V, E), n = 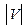 , m =
, m = 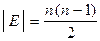 .
.
Кожне ребро ek Î E з’єднує пару вершин vi, vj Î V, які є його кінцями ці вершини граничні. Розрізняють початкову вершину з якої дуга виходить та кінцеву вершину , в яку дуга входить. Дві вершини (граничні вершини) які з’єднані двома або більше ребрами називаються кратними.
В загальному випадку граф може містити і ізольовані вершини які не є граничними вершинами ні з одним з ребер.
Кожному неорієнтованому графу можна поставити у відповідність орієнтований граф з тією самою множиною вершин, в якій кожне ребро замінено двома орієнтованими ребрами, що є інцидентними тим самим вершинам і мають зворотні напрямки. Таку відповідь будемо називати канонічною.
Граф, що має як ребра, так і дуги, називається мішаним.
Інцидентність. Задання графа за допомогою матриці інцидентності.
Задати граф означає задати множини його вершин і ребер, а також відношення інцидентності. Коли граф G — скінченний, тоді вершини даного графа v1 ,v2,,..., vn, а його ребра е1, е2,..., еm. Відношення інцидентності можна означити матрицею S= 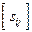 , що має n рядків й т стовпців. Рядки відповідають вершинам графа, а стовпці відповідають його ребрам. Якщо вершина vi є інцидентною ребру ео, , то sij = 1, в іншому випадку sij = 0. Це матриця інцидентності звичайного графа G, яка є одним із способів його визначення (для графа на рис. 2).
, що має n рядків й т стовпців. Рядки відповідають вершинам графа, а стовпці відповідають його ребрам. Якщо вершина vi є інцидентною ребру ео, , то sij = 1, в іншому випадку sij = 0. Це матриця інцидентності звичайного графа G, яка є одним із способів його визначення (для графа на рис. 2).
Sij = 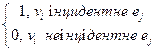
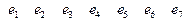
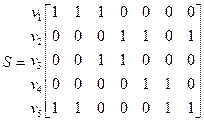 ;
;
У матриці інцидентності 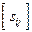 орієнтованого графа G, якщо вершина vi —початок ребра ej, то sij = 1; якщо vi: - кінець ej, то sij = -1. Кількість одиниць у рідку дорівнює степені відповідній вершині (для орграфа кількість позитивних одиниць визначає позитивну степінь, а кількість від’ємних одиниць - від’ємну степінь). Нульовий рядок відповідає ізольованій вершині, а нульовий стовпець - петлі.
орієнтованого графа G, якщо вершина vi —початок ребра ej, то sij = 1; якщо vi: - кінець ej, то sij = -1. Кількість одиниць у рідку дорівнює степені відповідній вершині (для орграфа кількість позитивних одиниць визначає позитивну степінь, а кількість від’ємних одиниць - від’ємну степінь). Нульовий рядок відповідає ізольованій вершині, а нульовий стовпець - петлі.
Треба мати на увазі, що нульовий стовпець матриці інцидентності лише вказує на присутність петлі, але не містить відомостей про те, з якою вершиною зв’язана ця петля.
Sij = 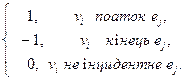
Sij = 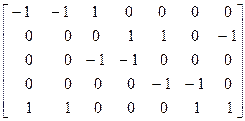 .
.
Відношення інцидентності можна задати ще списком ребер графа. Кожний рядок цього списку відповідає ребру, в ньому записано номери вершин, інцидентних йому. Для неорієнтованого графа порядок цих вершин у рядку довільний, для орієнтованого першим записується номер або інше найменування початку ребра, а другим — його кінця. У таблицяхнаведено списки ребер для графів, зображених на рис. 2 та 3.
Таблиця 1
| Ребра | e1 | e2 | e3 | e4 | e5 | e6 | e7 |
| Вершини | v1 | v1 | v1 | v2 | v2 | v4 | v2 |
| v5 | v5 | v3 | v3 | v4 | v5 | v5 |
Дата добавления: 2016-07-27; просмотров: 6348;











