його вершин сполучається ребром.

У звичайного повного графа Р_п на п вершинах степені всіх вершин однакові й дорівнюють п - 1.

Степінь ізольованої вершини r (v_i) = 0. Вершина зі степеню r (v_i) = 1 називається кінцевою чи висячою вершиною.

Степені вершин орієнтованих графів

Частини графа, суграфи та підграфи

Означення.Граф G`= (V`, E`) - називається частиною графа G = (V, E) (G`Ì G), якщо мно­жина його вершин V` міститься в множині V, а множина Е` ре­бер - в Е. Якщо V` = V, то частина графа називається су- графом.

Наприклад, існує нульовий суграф, множина ребер якого є порожньою. Суграф G` покриває вершини неорієнтованого графа G (або є покривним), якщо будь-яка вершина останнього — інцидентна хоча б одному ребру з G`. Таким чином, якщо в графі G існує ізольована вершина v, не інцидент­на жодному ребру, то покривного суграфа цього графа не існує.

Означення. Граф G`= (V`, E`) - називається частиною графа G = (V, E) (G`Ì G), якщо V` Ì V та E` Ì E, тобто граф містить усі вершини і ребра будь-якої його частини. Частина, яка містить певну підмножину ребер графа та усі інцидентні їм вершини, називається підграфом або компонентом вихідного графа..

Сукупність усіх ребер графа, які не належать його підграфу (разом з інцидентними вершинами) , утворюють доповнення підграфа.

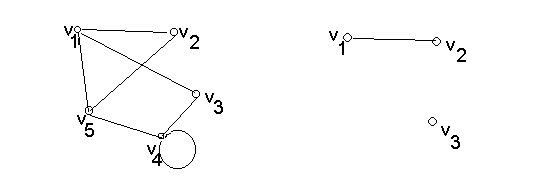
а б

Рис. 7.1. Граф та його частини:

а - граф; б - частина графа;

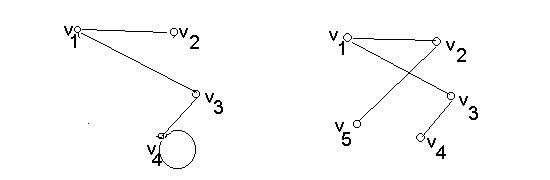
в г

Рис. 7.2. Граф та його частини:

в - підграф; г - суграф.

Приписування вершинам, ребрам та дугам графа деяких кількісних ознак або характерних властивостей називається. вагою і дозволяє отримати зважений граф.

Велике значення для моделювання мають зважені орієнтовані графи, які називаються. сигнальними графами.

Вершини сигнального графа ототожнюються з будь-якою змінною, яка характеризує стан системи, вага кожної вершини означає функцію часу або інші величини, які характеризують відповідні змінні.

Дуги відображають зв’язок між змінними а вага дуги представляє собою кількісне чи функціональне відношення, яке характеризує передачу сигналу від однієї вершини до другої.

Маршрути, цикли, зв’язність.

Інколи на графі необхідно виділити маршрут довжиною m.

МаршрутомMу заданому графі G = (V, Е) називається скінченна послідовність його ребер, яка має вигляд

(v₁, v₂), (v₂,, v₃), ..., (v_m-1, v_m).

Число m ребер маршруту M називається довжиною цього маршруту. Часто можна зустріти і таке означення маршруту в графі: послі­довність вершин

v₁, v₂, ..., v_m графа G = (V, Е) називається марш­рутом M,який з'єднує вершини v₁ і v_m.. В обох випадках вершини v₁, v₂, ..., v_m називаються вершинами маршруту.

Очевидно, що відношення маршрут, який з'єднує вершини., є симетричним і транзитивним.

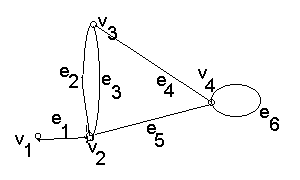
Рис. 8. Граф.

Прикладами маршрутів на графі рис.8 може бути послідовність {e₁, e₂, e₃, e₂, e₄ }, {e₄, e₆, e₅}. Перший маршрут проходить через послідовність вершин {v₁, v₂, v₃, v₂, v₃, v₄ } і з’єднує вершини v₁ і v₄ , а другий - через послідовність вершин {v₃, v₄, v₄ } і з’єднує вершини v₃, v₄ .

Замкнутий маршрут приводить в ту ж вершину, з якої почався.

Маршрут називається ланцюгом,якщо всі його ребра різні, і простим ланцюгом,якщо всі його вершини, крім, можливо, пер­шої і останньої, різні.

Так на графі рис.8. {e₂, e₄, e₆} - ланцюг, {e₁, e₂, e₄} - простий ланцюг.

Маршрут називається циклічним,якщо перша і остання його вершини збігаються.

Цикломназивається циклічний ланцюг, а простим циклом-простий циклічний ланцюг. Так на графі рис.8. {e₂, e₄, e₅} - простий цикл.

Граф називається ациклічним графом,якщо в ньому відсутні цикли. Безпосередньо з означення маршруту і циклу випливають такі твердження.

Твердження 1.Будь-який маршрут, який з'єднує які-небудь дві вершини графа, має простий ланцюг, що з'єднує ці вершини.

Твердження .2. Будь-який цикл в графі має простий цикл.

Дві вершини v_i і v_j називаються зв'язаними, якщо існує маршрут вигляду (v₁, v₂), (v₂,, v₃), ..., (v_m-1, v_m) із кінцями v_i та v_j. Граф називається зв'язним, якщо будь-яка пара його вершин є зв'язаною.

Довжина найменшого ланцюга між вершинами v_i і v_j зви­чайного зв'язного графа G називається відстанню d(v_i, v_j) між: цими вершинами.