Смешанные системы счисления

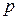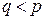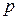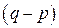В смешанной системе счисления числа, заданные в системе счисления с основанием , изображаются с помощью цифр другой системы счисления с основанием по следующему правилу: каждый коэффициент p-ичного разложения записывается в q-ичной системе. При этом называется старшим основанием, а – младшим основанием, а сама смешанная система называется -ичной. При этом 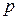называется старшим основанием, а – младшим основанием, а сама смешанная система называется 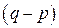-ичной. Для того чтобы запись числа в смешанной системе была однозначной, для представления любой p-ичной цифры отводится одно и то же количество q-ичных разрядов, достаточное для представления любого базисного числа p-ичной системы. Так, в смешанной двоично-десятичной системе счисления для изображения каждой десятичной цифры отводится четыре двоичных разряда. Здесь имеется избыточность, т.к. двоичная тетрада позволяет изобразить не 10, а 16 чисел, и следовательно, существует целый ряд двоично-десятичных систем, отличающихся весами двоичных разрядов внутри одной тетрады. В наиболее часто используемой (2-10)-ной системе веса двоичных разрядов внутри тетрады естественны, т.е. 8 – 4 – 2 – 1.

Пример

.

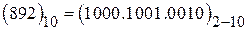Существуют и другие варианты двоично-десятичного кода. Например, двоично-десятичные коды с весами 5 – 1 – 2 – 1 и 2 – 4 – 2 – 1 широко используются при поразрядном уравновешивании в цифровых измерительных приборах.

В контрольной работе веса разрядов в тетраде естественные (8-4-2-1).

В смешанных системах счисления особого внимания заслуживает случай, когда

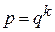, (2.3)

где 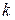– целое положительное число. В этом случае запись какого-либо числа в смешанной системе совпадает с изображением этого числа в системе с основанием .

Примеры

1) ;

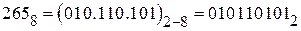2) .

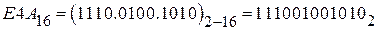В обоих случаях условие (2.3) выполняется: в первом – 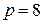, , 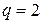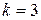; во втором – 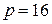, , 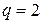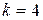. Справедливость полученных равенств легко проверяется если по (2.1) найти десятичные эквиваленты для исходного числа и его отображения в двоичном коде.