Понятия о линейных и угловых перемещениях

При изгибе

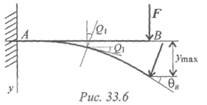
Под действием поперечных нагрузок продольная ось искривля­ется (рис. 33.6). Если материал подчиняется закону Гука, после сня­тия нагрузок брус выпрямляется, поэтому изогнутую ось бруса на­зывают упругой линией. По форме упругой линии балки можно су­дить о перемещениях при изгибе.

При прямом поперечном изгибе бруса его ось, искривляясь, остается

в силовой плоскости. В результате деформации бруса каждое из его поперечных сечений получает вертикальное и горизонтальное перемещение, а само сечение поворачивается на некоторый угол θ.

Деформации должны иметь упру­гий характер, они достаточно малы. В этом случае горизонтальные пе­ремещения сечений ничтожно малы и не учитываются. Рассматривают вертикальные перемещения центра тяжести сечения, называемые про­гибами (у). Максимальные прогибы обозначают f = у_max. Для обеспече­ния нормальной работы устанавливаемого на балках оборудования проводят расчет на жесткость.

Условие жесткости выражается неравенством

f ≤ [ f ],

где f — максимальный расчетный прогиб балки; [f] — допускаемый прогиб.

Иногда проверяется угол поворота сечения θ < [θ].

Допускаемый прогиб невелик: от 1/200 до 1/1000 пролета балки; допускаемый угол поворота 1·10^-3 рад.

Существует несколько методов определения перемещений сече­ний при изгибе. Один из них основан на дифференцировании урав­нения упругой линии, более рациональный способ — использование интегралов Мора. Метод Мора — универсальный способ определе­ния линейных и угловых перемещений в любых системах.

Для облегчения расчетов на жесткость можно использовать формулы прогибов и углов поворота сечений балок для простейших случаев нагружений. Наиболее распространенные случаи нагружения и расчетные формулы приведены в таблице.

При решении используем принцип независимости действия сил. Заданный случай нагружения делится на составляющие, для кото­рых прогибы рассчитываются по известным табличным формулам, результаты расчетов суммируются.

Ограничение угла поворота вводится для обеспечения нормаль­ной работы подшипников скольжения и роликовых подшипников.

В этом случае проверяется дополнительное условие жесткости: