Расчет круглого бруса на изгиб с кручением
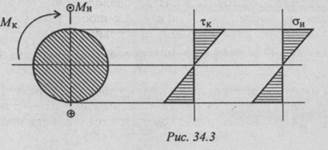
Вслучае расчета круглого бруса при действии изгиба и кручения (рис. 34.3) необходимо учитывать нормальные и касательные напряжения, т. к. максимальные значения напряжений в обоих случаях возникают на поверхности. Расчет следует вести по теории прочности, заменяя сложное напряженное состояние равноопасным простым.
Максимальное напряжение кручения в сечении 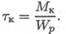
Максимальное напряжение изгиба в сечении 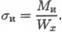
По одной из теорий прочности в зависимости от материала бруса рассчитывают эквивалентное напряжение для опасного сечения и проверяют брус на прочность, используя допускаемое напряжение изгиба для материала бруса.
Для круглого бруса моменты сопротивления сечения следующие:
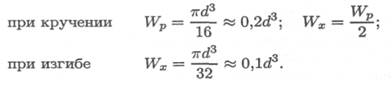
При расчете по третьей теории прочности, теории максимальных касательных напряжений, эквивалентное напряжение рассчитывается по формуле 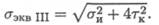
Теория применима для пластичных материалов. При расчете по теории энергии формоизменения эквивалентное напряжение рассчитывается по формуле
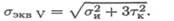
Теория применима для пластичных и хрупких материалов. Эквивалентное напряжение при расчете по теории максимальных касательных напряжений:
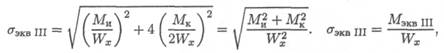
где Мэкв III = √Ми² + Мк²— эквивалентный момент.
Условие прочности:
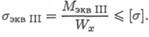
Эквивалентное напряжение при расчете по теории энергии формоизменения:
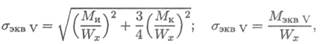
где Мэкв v = √Ми² + 0,75Мк²— эквивалентный момент.
Условие прочности:
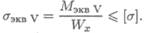
Дата добавления: 2019-02-08; просмотров: 758;











