Расчет по формуле Эйлера

Задачу определения критической силы математиче­ски решил Л.Эйлер в 1744 г.

Для шарнирно закрепленного с обеих сторон стержня (рис. 36.2) формула Эйлера имеет вид

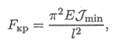
где Е — модуль упругости;

Jmin — минимальный осевой момент инерции стержня;

l — длина стержня.

Потеря устойчивости происходит в плоскости наи­меньшей жесткости, поэтому в формулу входит минимальный из осевых моментов инерции сечения (J_X или J_y).

Формулу распространили на другие формы закрепления стерж­ней, рассмотрев форму потери устойчивости в каждом случае.

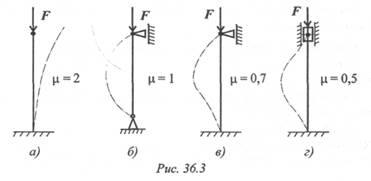
Длина стержня заменяется ее приведенным значением, учиты­вающим форму потери устойчивости в каждом случае: l_Прив = μl, где μ — коэффициент приведения длины, зависящий от способа за­крепления стержня (рис. 36.3).

Формула для расчета критической силы для всех случаев

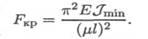
Критические напряжения.

Критическое напряжение — напряжение сжатия, соответству­ющее критической силе.

Напряжение от сжимающей силы определяется по формуле

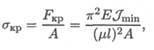
где σ_кр — напряжение сжатия, при котором стержень еще устойчив. Корень квадратный из отношения минимального момента инерции сечения к площади поперечного сечения принято называть мини­мальным радиусом инерции imin:

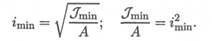
Тогда формула для расчета критического напряжения перепи­шется в виде

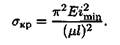
Отношение μl / imin носит название гибкости стержня λ.

Гибкость стержня — величина безразмерная, чем больше гиб­кость, тем меньше напряжение:

Заметим, что гибкость не зависит от материала, а определяется только геометрией стержня.